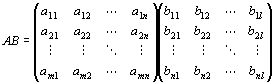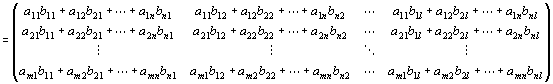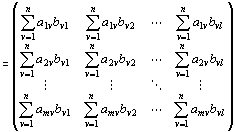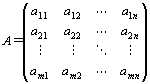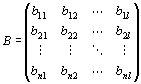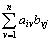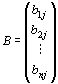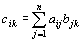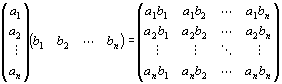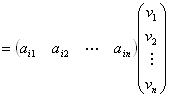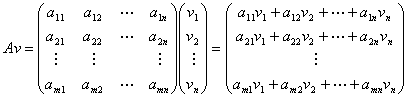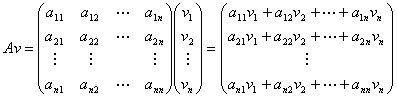実行列の積の定義　―　トピック一覧

・定義：行ベクトルと列ベクトルの積 / 行列の積 [ 例：(n,1)型と(1,n)型/(m,n)型と(n,1)型/(n,n)型と(n,1)型]
・定義：行列のべき乗

※実行列関連ページ：実行列の定義/正方行列に関する様々な定義/行列の和･スカラー倍の定義/行列積の性質/逆行列･正則行列･特異行列の定義/転置行列の性質/行列の代数系
※上位概念：体上の行列の積の定義　　
※線形代数目次・総目次

定義：実行列の積−もっとも単純なケース−行ベクトルと列ベクトル


設定


R：実数をすべて集めた集合（実数体）　

[文献]
・永田『理系のための線形代数の基礎』1.4(p.24);
・藤原『線形代数』2.1(p.24);
・『高等学校代数幾何』(p.86);
・戸田山田『計量経済学の基礎：統計的手法の理論とプログラミング』2.2.2(p.58)
・グリーン『計量経済分析』2.3.4(p.14) ;松坂『解析入門4』15.1-C (p. 4)

まえがき

実n次元横ベクトルと、実n次元縦ベクトルも、実行列の一例であった（∵）。
そこで、
行列の積の定義の、もっとも単純な例として、
実n次元横ベクトルと実n次元縦ベクトルの積の定義を示し、
行列の積の定義の導入とする。

本題

・横ベクトルAと縦ベクトルBとの間に積ABが定義されるのは、
　両者が、実n次元横ベクトルと実n次元縦ベクトルである場合だけ。
　両者の次数が一致しない場合は、積を定義不能とする。　
・実n次元横ベクトルA=(a1,a2,…,an)と　
　実n次元縦ベクトル　　
　　
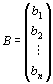
　との積ABは、次のように定義される。
　　
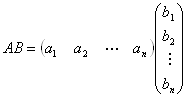
　　　　=a1b1＋a2b2＋a 3b3＋…＋an bn　
　　　　　　　　　（ここでの和･積は実数体Rに定められている和積）　
　　　　

活用例

　

→[トピック一覧：行列積の定義]
→線形代数目次・総目次

 　

定義：行列の積


設定


R：実数をすべて集めた集合（実数体）　
A, B ：実行列　

[文献]
・『岩波数学辞典』83行列B(pp.219-220);
・永田『理系のための線形代数の基礎』1.4(p.24);
・斎藤『線形代数入門』2章§1(p.33);
・藤原『線形代数』2.1(p.24);
・『高等学校代数幾何』(p.86);
・グリーン『計量経済分析』2.3.4(p.14);
・高橋『経済学とファイナンスのための数学』(p.17);
・戸田山田『計量経済学の基礎：統計的手法の理論とプログラミング』2.2.2(p.59)
・松坂『解析入門4』15.1-C (p. 4)
・
・

本題

・実行列の積ABが定義されるのは、〈Aの列の個数〉と〈Bの行の個数〉とが一致する場合だけ。
　〈Aの列の個数〉と〈Bの行の個数〉とが一致しない場合は、実行列の積ABは、考えない。

・(m,n)型行列Aと(n,l)型行列Bとの積ABは、次の(m,l)型行列として定義される。　　　
　　
　　
　　　
　つまり、
　(m,n)型行列　
　　　　
　と
　(n,l)型行列　
　　　　　
　との積ABとは、
　あらゆる i行j列成分(AB)ij　(i=1,2,…,m, j=1,2,…,l )　を、　　
　　　
　　　　=ai1b1j＋ai2b2j＋ai 3b3 j＋…＋ain bnj　
　　　　　　　　　（ここでの和･積は実数体Rに定められている和積）　
　によって定めた(m,l)型行列である。
　　※要するに、積ABの i行j列成分(AB)ij　(i=1,2,…,m, j=1,2,…,l, )は、
　　　Aのi行とBのj列を取り出して、
　　　 n次元横ベクトルになっているAのi行(ai1,ai2,…,ain)と、
　　　 n次元縦ベクトルになっているBのj列
　　　　　　
　　　との積を計算したもの。
・上記の定義は、多くの教科書で、次のように略記されている。　
　(m,n)型行列A=(aij), (n,l)型行列B=(bjk)にたいして、　　
　AB=(cik)　ただし、
　　　　　　　　

例

[実n次元横ベクトルと実n次元縦ベクトルとの行列積]
・実n次元横ベクトルA=(a1,a2,…,an)と、実n次元縦ベクトルB= t (b1,b2,…,bn) との行列積ABは定義可能。
　なぜなら、　
　Aが1行n列行列、Bがn行1列の行列であって、
　〈Aの列の個数〉と〈Bの行の個数〉とがnで一致するから。　
・行列積ABは、(1,n)型行列と(n,1)型行列との行列積だから、(1,1)型行列、すなわち単なる実数、となる。
・行列積の計算結果→詳細　

例

[実n次元縦ベクトルと実n次元横ベクトルとの行列積]
・実n次元縦ベクトルA= t (a1,a2,…,an) と実n次元横ベクトルB= (b1,b2,…,bn) との行列積ABは
　定義可能。　
　なぜなら、　
　Aがn行1列行列、Bが1行n列の行列であって、
　〈Aの列の個数〉と〈Bの行の個数〉とが一致して、1であるから。　
・行列積ABは、(n,1)型行列と(1,n)型行列との行列積だから、(n,n)型行列となる。
・行列積ABの i行j列成分(AB)ij　(i=1,2,…,n, j=1,2,…,n )は、
　横ベクトルとなっているAのi行と、縦ベクトルとなっているBのj列との、積を、
　計算したものとなるが、　
　Aのi行は1次元横ベクトル（単なる実数）ai　、
　Bのj列も1次元縦ベクトル（単なる実数）bj　　
　であるから、　　　　。
　(AB)ij　=　aibj　　
・以上から、
　　

[文献]
・『高等学校代数幾何』(p.86);
・グリーン『計量経済分析』2.3.6(p.19)

例

[(m,n)型行列と実n次元縦ベクトルとの行列積]
・(m,n)型行列Aと実n次元縦ベクトルv= t (v1,v2,…,vn) との行列積A vは定義可能。　
　なぜなら、　
　Aがm行n列行列、vがn行1列の行列であって、
　〈Aの列の個数〉と〈vの行の個数〉とが一致して、nであるから。　
・行列積A vは、(m,n)型行列と(n,1)型行列との行列積だから、(m,1)型行列すなわち実m次元縦ベクトルとなる。
・行列積A vの i行成分( A v )i　(i=1,2,…,m)は、
　横ベクトルとなっているAのi行と、縦ベクトルvとの、積を、計算したものとなるが、　
　Aのi行は n次元横ベクトル(ai1,ai2,…,ain)　、
　vは n次元縦ベクトルt (v1,v2,…,vn)　
　であるから、
　( A v )i　
　
　= ai1 v1＋ai2 v2＋…＋ain vn　　（ここでの和･積は実数体Rに定められている和積）
・以上から、
　

※

活用例：一次写像f:Rn→Rmの表現行列/一次写像f:V→Wの表現行列　

例

[(n,n)型行列と実n次元縦ベクトルとの行列積]
・(n,n)型行列Aと実n次元縦ベクトルv= t (v1,v2,…,vn) との行列積A vは定義可能。　
　なぜなら、　
　Aがn行n列行列、vがn行1列の行列であって、
　〈Aの列の個数〉と〈vの行の個数〉とが一致して、nであるから。　
・行列積A vは、(n,n)型行列と(n,1)型行列との行列積だから、(n,1)型行列すなわち実n次元縦ベクトルとなる。
・行列積A vの i行成分( A v )i　(i=1,2,…,n)は、
　「横ベクトルとなっているAのi行」と「縦ベクトルv」との積を、計算したものとなるが、　
　Aのi行は n次元横ベクトル(ai1,ai2,…,ain)　、
　vは n次元縦ベクトルt (v1,v2,…,vn)　
　であるから、
　( A v )i　
　
　= ai1 v1＋ai2 v2＋…＋ain vn　　（ここでの和･積は実数体Rに定められている和積）
・以上から、
　　

※

活用例：一次変換f:Rn→Rnの表現行列/一次変換f:V→Vの表現行列　

→[トピック一覧：行列積の定義]
→線形代数目次・総目次

[yahoo:yoko]

定義：行列のべき乗


設定


R：実数をすべて集めた集合（実数体）　
A ：正方行列　

本題

・正方行列Aのそれ自身との行列積AAを、A2と表す。
・同様に、正方行列Aのそれ自身との行列積AAAをA3、
　　　　　正方行列Aのそれ自身との行列積AAAAをA4、
　　　　　：　　　　
　と表す。

※

活用例：ベキ等行列
性質：べき乗の計算　

→[トピック一覧：行列積の定義]
→線形代数目次・総目次

　

(reference)
日本数学会編集『岩波数学辞典（第三版）』 岩波書店、1985年、項目83行列(pp.219-)
線形代数のテキスト
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、1.4行列と一次写像(pp.23-6)。
佐武一郎『線形代数学(第44版)』裳華房、1987年、I.ベクトルと行列の演算§2-3行列の演算(pp.4-16)。
砂田利一『現代数学への入門：行列と行列式』2003年、§2.2一般の行列(pp.54-60)、§2.3行列の演算(pp.60-65)、§2.4行列の操作(pp.66-70).
藤原毅夫『理工系の基礎数学2：線形代数』岩波書店、1996年、2.1行列の定義と演算(pp.21-29)。
斎藤正彦『線形代数入門』東京大学出版会、1966年、第2章行列§1行列の定義と演算(pp.31-40)。

ホフマン・クンツェ『線形代数学I』培風館、1976年、一次方程式(pp.1-27)。
志賀浩二『数学30講シリーズ：線形代数30講』朝倉書店、1988年、17講線形写像と行列(pp.107-112)。
数理経済学のテキスト
西村和雄『経済数学早わかり』日本評論社、1982年、２章線形代数§2行列と行列式(pp.46-72)。
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、5章行列(pp.161-199):一次写像の行列表現を中心にしている。
William H. Greene（斯波・中妻・浅井訳） 『経済学体系シリーズ：グリーン計量経済分析I：改訂4版』エコノミスト社、2000年、第２章行列代数2.2行列の用語(pp.10-12);2.3行列の算法(pp.12-21)。
岩田暁一『経済分析のための統計的方法(第2版)』東洋経済新報社、1983年、12.1行列の演算(pp.269-277);12.4.2逆行列(pp.294-5)。

　

→[トピック一覧：行列積の定義]
→線形代数目次・総目次