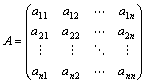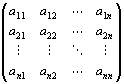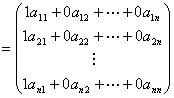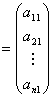実行列の積の性質　―　トピック一覧

・定理：行列積は可換則を満たさない/積の結合則/積の分配則/行列積とスカラー積の混合/零行列との積
・定理：行列積の各列/行列と基本ベクトルとの積/行列のべき乗の計算　

※実行列関連ページ：実行列の定義/正方行列に関する様々な定義/行列和･スカラー倍の定義/行列積の定義/逆行列･正則行列･特異行列の定義/転置行列の性質/行列の代数系
※上位概念：体上の行列積の性質
※線形代数目次・総目次

定理：行列積は可換則を満たさない　

設定

R：実数をすべて集めた集合（実数体）　
A, B ：実行列　

[文献]
・斎藤『線形代数入門』2章§1(p.34);
・藤原『線形代数』2.1(p.25);
・『高等学校代数幾何』(p.83);
・グリーン『計量経済分析』2.3.4(p.15) ;
・戸田山田『計量経済学の基礎：統計的手法の理論とプログラミング』2.3.1(p.64)

本題

・実行列の積について、可換則は成立しない。
　つまり、「任意の(m,n)型実行列A、(n,l)型実行列Bに対して、AB=BAとなる」とはいえない。
　　　　　AB=BAを満たさない、(m,n)型行列A・(n,l)型行列Bの組が、存在する。
・そもそも、m≠lの場合、
　(m,n)型実行列A、(n,l)型実行列Bに対して、積ABは定義できても、積BAは定義できない。
　（積BAの定義は、Bの列数lとAの行数mの一致を要請するが、
　　　　m≠lの場合これが満たされないから、積BAは定義不能。）　　
・m=lの場合でも、(m,n)型実行列A、(n,l)型実行列Bに対して、AB=BAとならないケースがある。
　たとえば、
　　
・AB=BAが成り立つ場合、「AとBとは交換可能」という。[藤原『線形代数』2.1(p.25);]　

→[トピック一覧：実行列の積の性質]
→線形代数目次・総目次

定理：行列の積の結合則

設定

R：実数をすべて集めた集合（実数体）　
A, B, C ：実行列　

[文献]
・『岩波数学辞典』83行列B(pp.219-220);
・永田『理系のための線形代数の基礎』1.4(p.25);
・斎藤『線形代数入門』2章§1(p.34);
・藤原『線形代数』2.1(p.26);
・『高等学校代数幾何』(p.83;86);
・グリーン『計量経済分析』2.3.4(p.17) ;
・松坂『解析入門4』15.1-C命題1 (p. 5) ;
・戸田山田『計量経済学の基礎：統計的手法の理論とプログラミング』2.3.1(p.64)

本題

実行列の積は、結合則を満たす。　
すなわち、
　任意の(m,n)型実行列A、(n,l)型実行列B、(l,k)型実行列Cに対して、
　「『AとBの積』とCとの積」は、「Aと『BとCとの積』との積」と等しい。
　　　　　(AB)C=A(BC)　　

※

可換則は成り立たないことに注意。

※

なぜ→証明　

→[トピック一覧：実行列の積の性質]
→線形代数目次・総目次

定理：行列の積の分配則

設定

R：実数をすべて集めた集合（実数体）　
A, B, C ：実行列　

[文献]
・『岩波数学辞典』83行列B(pp.219-220);
・永田『理系のための線形代数の基礎』1.4(p.25);
・斎藤『線形代数入門』2章§1(p.34);
・藤原『線形代数』2.1(p.26);
・『高等学校代数幾何』(p.83;86);
・グリーン『計量経済分析』2.3.4(p.17) ;
・松坂『解析入門4』15.1-C命題3 (p. 6) ;
・戸田山田『計量経済学の基礎：統計的手法の理論とプログラミング』2.3.1(p.64)

本題

実行列の積は、分配則を満たす。　
すなわち、
・任意の(m,n)型実行列A、(n,l)型実行列B,Cに対して、
　　　A(B＋C)=AB＋AC　　
・任意の(m,n)型実行列A,B、(n,l)型実行列Cに対して、
　　　(A＋B)C=AC＋BC　　

※

可換則は成り立たないことに注意。

→[トピック一覧：実行列の積の性質]
→線形代数目次・総目次

定理：行列積とスカラー積

設定

R：実数をすべて集めた集合（実数体）
A, B ：実行列　
c：実数

[文献]
・斎藤『線形代数入門』2章§1問2(p.34);

本題

任意の「(m,n)型実行列」A、「(n,l)型実行列」B、実数cに対して、
　　　c(AB)=(cA)B=A(cB)　　

※

行列の積については、可換則は成り立たないから、
AとBの位置は入れ替えられないことに注意。

→[トピック一覧：実行列の積の性質]
→線形代数目次・総目次

定理：零行列との積

設定

R：実数をすべて集めた集合（実数体）　
A ：実行列　

[文献]
・斎藤『線形代数入門』2章§1(p.34);

本題

　任意の(m,n)型実行列Aと、零行列との積は、零行列。
　AO_n,l＝O_m,l 　　
　O_l,m A＝O_l,n 　

→[トピック一覧：実行列の積の性質]
→線形代数目次・総目次

定理：行列積の各列

設定

R：実数をすべて集めた集合（実数体）
A, B ：実行列　　

[文献]
・斎藤『線形代数入門』2章§1-4^〇(pp.35-36)

本題

任意の(m,n)型実行列A、(n,l)型実行列Bに対して、
　・「行列積ABの第1列」＝「実行列Aと『実行列Bの第1列』との行列積」
　・「行列積ABの第2列」＝「実行列Aと『実行列Bの第2列』との行列積」
　：　　　　　　　：　　　　　　　　　　　　　　　　：
　・「行列積ABの第l列」＝「実行列Aと『実行列Bの第l列』との行列積」
が成り立つ。　　

→[トピック一覧：実行列の積の性質]
→線形代数目次・総目次

定理：行列と基本ベクトルとの積

任意の実n次正方行列
　　
と基本ベクトルe₁, e₂,…, e_nとの行列積について、以下が成り立つ。
　・A e₁＝「Aの第1列」
　・A e₂＝「Aの第2列」
　：　　　　　　　：
　・A e_n＝「Aの第n列」

※活用例：
　・一次写像による基本ベクトルの像
　・対角行列であるための必要十分条件―固有値固有ベクトルの観点　

※なぜ？→行列積の計算をすればわかる。
　・A e₁＝　　
　　　　
　　　　
　　　　
　　　　＝「Aの第1列」　　
　・A e₂＝「Aの第2列」
　：　　　　　　　：
　・A e_n＝「Aの第n列」
　も同様に。　　

→[トピック一覧：実行列の積の性質]
→線形代数目次・総目次

定理：行列の冪の計算

[文献]
・志賀『線型代数30講』29講TeaTime(p.187)
・戸田山田『計量経済学の基礎：統計的手法の理論とプログラミング』問題2.24(pp.110-111);

1.

[対角行列のべき乗]
実n次正方行列Aが対角行列 diag(λ₁,λ₂,…,λ_n)であるならば、
　つまり、
　　　　　
　ならば、
A^k= diag(λ^k₁,λ^k₂,…,λ^k_n)　　　
　　　
　　　
※なぜ？→→行列積の計算をすればわかる。

2.

[対角化可能な行列のべき乗]
実n次正方行列Aが n次正則行列Pによって diag(λ₁,λ₂,…,λ_n)に対角化可能ならば、
　すなわち、実n次正方行列Aに対して、P^−１AP= diag(λ₁,λ₂,…,λ_n)を満たす n次正則行列Pが存在するならば、
A^k=P diag(λ^k₁,λ^k₂,…,λ^k_n) P^−１　　　

※なぜ？
　・P^−１AP= diag(λ₁,λ₂,…,λ_n)⇔A=P diag(λ₁,λ₂,…,λ_n) P^−１　
　・だから、
　　　実n次正方行列Aが n次正則行列Pによって diag(λ₁,λ₂,…,λ_n)に対角化可能ならば、
　　　A=P diag(λ₁,λ₂,…,λ_n) P^−１　であるから、
　　　A^k=（P diag(λ₁,λ₂,…,λ_n) P^−１）（P diag(λ₁,λ₂,…,λ_n) P^−１）…（P diag(λ₁,λ₂,…,λ_n) P^−１）
　　　　＝P diag(λ₁,λ₂,…,λ_n) （ P^−１P） diag(λ₁,λ₂,…,λ_n) （ P^−１P）…（ P^−１P） diag(λ₁,λ₂,…,λ_n) P^−１　∵行列積の結合則　
　　　　＝P diag(λ₁,λ₂,…,λ_n) I_n diag(λ₁,λ₂,…,λ_n) I_n…I_n diag(λ₁,λ₂,…,λ_n) P^−１　　∵逆行列の定義　
　　　　= P （ diag(λ₁,λ₂,…,λ_n))^k P^−１　　　
　　　　＝P diag(λ^k₁,λ^k₂,…,λ^k_n) P^−１　∵上記1[対角行列のべき乗]から。　

3.

実n次正方行列Aが、n個の一次独立な固有ベクトルを有すならば、A^k=P diag(λ^k₁,λ^k₂,…,λ^k_n) P^−１　　

※なぜ？→行列対角化の条件と、上記2[対角化可能な行列のべき乗]から。　

4.

実n次正方行列Aに、n個の相異なる固有値を有すならば、A^k=P diag(λ^k₁,λ^k₂,…,λ^k_n) P^−１　　

※なぜ？→行列対角化の条件と、上記2[対角化可能な行列のべき乗]から。　

→[トピック一覧：実行列の積の性質]
→線形代数目次・総目次

→[トピック一覧：実行列の積の性質]
→線形代数目次・総目次