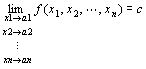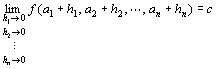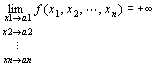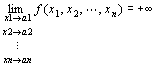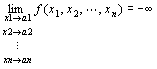|
|
|
定義: n変数関数の収束convergence・極限値limit |
|
→ はじめに読むべき定義/ε-δ論法による定義/近傍概念による定義 |
|
はじめに
読むべき
定義 |
「 n次元空間Rn上の点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
関数f (P) = f (x1,x2,…,xn)が実数cに収束する」
「 n次元空間Rn上の点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたときの、
関数f (P) = f (x1,x2,…,xn)の極限値は実数cである」
f ( P )→c ( P → A )
f ( x1 , x2 ,…, xn )→c ( x1→a1 , x2→a2 ,… ,xn→an )
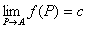 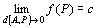
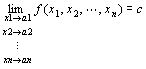 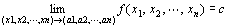
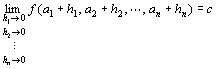
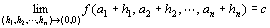
とは、
点P(x1,x2,…,xn)を、点A(a1,a2,…,an)と一致させることなく点A(a1,a2,…,an)に近づけたとき、
点P(x1,x2,…,xn)の点A(a1,a2,…,an)への接近経路にかかわらず、
関数f (P) = f (x1,x2,…,xn)の値が同じ1つの実数値cに近づくことをいう。
※留意点
(1)極限の定義において、点Pと点Aが一致することは除外している。
点Aが関数f (P) = f (x1,x2,…,xn)の定義域に含まれているとは限らない。
(2) 点Pの点Aへの接近経路によって、
関数f (P) = f (x1,x2,…,xn)が近づく値が異なるときには、
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
関数f (P) = f (x1,x2,…,xn)がcに収束しない」
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
関数f (P) = f (x1,x2,…,xn)に極限値は存在しない」という。
※この定義は一見わかりやすい。
ところが、「近づく」とはいかなる事態を指すのか、という点が、
明らかにされておらず、
この「収束」「極限」定義は、実のところは不正確で、
証明での使用に耐えられない。
そこで、
「近づく」の意味を明確化するために、
「収束」「極限」概念は、次のように厳密に定義される。 |
[ 具体例]
・1変数関数の収束・極限値
・2変数関数の収束・極限値
[ 一般化]
・実数値関数の極限
・ベクトル値関数の極限
・距離空間のあいだの写像の極限
[ 活用例]
n変数関数の連続性/偏微分
[ 文献]
杉浦
『解析入門I』I§6定義2-3(pp.51-2);
笠原『微分積分学』1.4[2](p.28);
黒田『微分積分学』定義8.6(p.277);
髙木『解析概論』9極限(p.20)
|
|
|
→ 「n変数関数の収束・極限の定義」先頭 |
|
|
厳密な
定義:
ε -δ
論法 |
「 n次元空間Rn上の点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
関数f (P) = f (x1,x2,…,xn)が実数cに収束する」
「 n次元空間Rn上の点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたときの、
関数f (P) = f (x1,x2,…,xn)の極限値は実数cである」
f ( P )→c ( P → A ) f ( x1 , x2 ,…, xn )→c ( x1→a1 , x2→a2 , xn→an )
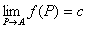 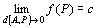
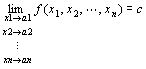 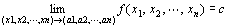
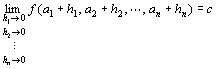
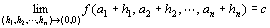
とは、
任意の(どんな)正の実数εに対して(でも)、ある正の実数δをとると、
0<d( P, A )<δ ⇒ d ( f (P), c )<ε
が成り立つ
ということ。
この定義を、論理記号で表せば、
(∀ε>0)(∃δ>0)(∀P∈Rn )(0< d ( P, A )<δ⇒ d ( f (P), c )<ε )
となる。
*d ( P, A )は、 n次元空間Rn上での点P(x1,x2,…,xn)と点A(a1,a2,…,an)との距離を、
d ( f (P), c )は、R上のf (P)とcとの距離| f (P)-c|を表す。 |
[ 文献]
小平『解析入門Ⅱ』p.259;
笠原『微分積分学』1.4[2](p.28);
吹田新保『理工系の微分積分学』pp.158-159.
高橋『経済学とファイナンスのための数学』p. 143;
髙木『解析概論』9極限(p.20) |
|
※ユークリッド距離が定められたユークリッド空間 Rnにおける極限概念
関数f (P) = f (x1,x2,…,xn)、すなわち、「 n次元空間Rnの部分集合から、実数体Rへの、写像」について、
収束・極限を扱う際には、
特別な目的がない限り、
n次元空間Rn上の距離をユークリッド距離で定めて、 n次元空間Rnをユークリッド空間Rnとし、
実数体Rの距離をユークリッド距離で定めて、Rを1次元ユークリッド空間Rとする、
設定のもとで考えるのが普通。
この設定下では、
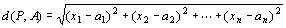
d ( f (P), c )=| f (P)-c|=| f (x1,x2,…,xn)-c|
だから、
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、関数f (P) = f (x1,x2,…,xn)が実数cに収束する」
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたときの、関数f (P) = f (x1,x2,…,xn)の極限値は実数cである」
の定義は、具体的には
┌任意の(どんな)正の実数εに対して(でも)、
|ある正の実数δが存在して、
| 「 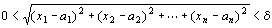
| ならば | f (x1,x2,…,xn)-c|<ε 」
└を成り立たせる
(∀ε>0)(∃δ>0)(∀x1,x2,…,xn∈R)(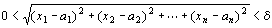 ⇒| f (x1,x2,…,xn)-c|<ε) ⇒| f (x1,x2,…,xn)-c|<ε)
となる。 |
|
※ n次元数ベクトル空間の上に定義されたユークリッド空間R2における極限概念
n次元空間Rnにベクトルの加法・スカラー乗法・自然な内積(標準内積)・ユークリッドノルム∥∥が定義されており、
n次元空間Rnを実n次元数ベクトル空間・計量実ベクトル空間・ノルム空間として扱える場合、
任意の実n次元数ベクトルx, y∈Rnのユークリッド距離は∥x-y∥ と表せる。
このユークリッド距離を定義したユークリッド空間Rnのもとでは、
d( P, A )=∥P-A∥
だから、
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、関数f (P) = f (x1,x2,…,xn)が実数cに収束する」
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたときの、関数f (P) = f (x1,x2,…,xn)の極限値は実数cである」
の定義は、具体的には
┌任意の(どんな)正の実数εに対して(でも)、
|ある正の実数δが存在して、
| 「 0<∥P-A∥<δ ならば | f (P)-c|<ε 」
|
└を成り立たせる
(∀ε>0)(∃δ>0)(∀P∈Rn )(0<∥P-A∥<δ⇒| f (P)-c|<ε )
と表せる。
ただし、上記のPは、「点P(x1,x2,…,xn)」を表す実n次元数ベクトル(x1,x2,…,xn)、
上記のAは、「点A(a1,a2,…,an)」を表す実n次元数ベクトル(a1,a2,…,an)
である。 |
|
|
→ 「n変数関数の収束・極限の定義」先頭 |
|
|
近傍を
用いた
定義 |
「 n次元空間Rn上の点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
関数f (P) = f (x1,x2,…,xn)が実数cに収束する」
「 n次元空間Rn上の点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたときの、
関数f (P) = f (x1,x2,…,xn)の極限値は実数cである」
f ( P )→c ( P → A ) f ( x1 , x2 ,…, xn )→c ( x1→a1 , x2→a2 , xn→an )
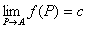 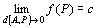
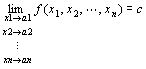 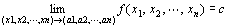
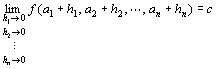
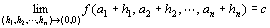
とは、
実数cの任意の(どんな)「R上のε近傍Uε(c)」に対して(でも)、
ある「Rn上の点Aの除外δ近傍U*δ(A)」が存在して、
f ( U*δ(A) ) ⊂Uε(c)
を満たす
ということ。
この定義を別の表現でいうと、
任意の(どんな)正の実数εに対して(でも)、ある正の実数δが存在して、
「 f ( U*δ(A) ) ⊂Uε(c) 」
すなわち「 (x,y)∈ U*δ(A) ならば、 f(x,y) ∈Uε(c)」
を成り立たせる、
ということ。
この定義を、論理記号で表せば、
(∀Uε(c))(∃ U*δ(A) )( f ( U*δ(A) ) ⊂Uε(c) )
(∀ε>0)(∃δ>0)( f ( U*δ(A) ) ⊂Uε(c) )
(∀ε>0)(∃δ>0)(∀P∈Rn )( P∈ U*δ(A) ⇒ f (P) ∈Uε(c))
となる。 |
[ 文献]
笠原『微分積分学』1.4[2](p.28);
|
|
※ユークリッド距離が定められたユークリッド空間 Rnにおける極限概念
関数f (P) = f (x1,x2,…,xn)、すなわち、「 n次元空間Rnの部分集合から、実数体Rへの、写像」について、
収束・極限を扱う際には、
特別な目的がない限り、
n次元空間Rn上の距離をユークリッド距離で定めて、 n次元空間Rnをユークリッド空間Rnとし、
実数体Rの距離をユークリッド距離で定めて、Rを1次元ユークリッド空間Rとする、
設定のもとで考えるのが普通。
この設定のもとでは、
点A(a1,a2,…,an)の「Rn上の点Aの除外δ近傍U*δ(A)」は、
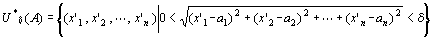
実数cの「R上のε近傍Uε(c)」は、(c-ε,c+ε)
だから、
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、関数f (P) = f (x1,x2,…,xn)が実数cに収束する」
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたときの、関数f (P) = f (x1,x2,…,xn)の極限値は実数cである」
の定義は、具体的には
┌任意の(どんな)正の実数εに対して(でも)、
|ある正の実数δが存在して、
| 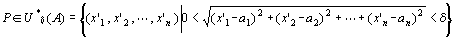
| ならば f (P)∈(c-ε,c+ε)
└を成り立たせる
となる。 |
|
※ n次元数ベクトル空間の上に定義されたユークリッド空間Rnにおける極限概念
n次元空間Rnにベクトルの加法・スカラー乗法・自然な内積(標準内積)・ユークリッドノルム∥∥が定義され、
n次元空間Rnを実n次元数ベクトル空間・計量実ベクトル空間・ノルム空間として扱える場合、
任意の実n次元数ベクトルx, y∈Rnのユークリッド距離は∥x-y∥ と表せる。
このユークリッド距離を定義したユークリッド空間Rnのもとでは、
点A(a1,a2,…,an)の「Rn上の点Aの除外δ近傍U*δ(A)」は、U*δ(A)={ Q∈Rn | 0<∥Q-A∥<ε }
実数cの「R上のε近傍Uε(c)」は、(c-ε,c+ε)
だから、
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、関数f (x,y)が実数cに収束する」
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたときの、関数f (x,y)の極限値は実数cである」
の定義は、
┌任意の(どんな)正の実数εに対して(でも)、
|ある正の実数δが存在して、
| P∈U*δ(A)={ Q∈Rn | 0<∥Q-A∥<ε }
| ならば
| f (P)∈(c-ε,c+ε)
└を成り立たせる
と表せる。
ただし、上記のPは、「点P(x1,x2,…,xn)」を表す実n次元数ベクトル(x1,x2,…,xn)、
上記のAは、「点A(a1,a2,…,an)」を表す実n次元数ベクトル(a1,a2,…,an)
である。 |
|
|
|
→ [トピック一覧:n変数関数の極限]
→総目次 |
|
|
定理: n変数関数の収束の、点列・数列の収束への言い換え |
| |
具体例: 1変数関数の収束の、数列の収束への言い換え/ 2変数関数の収束の、点列・数列の収束への言い換え
一般化:実数値関数の収束の、点列・数列の収束への言い換え/ベクトル値関数の収束の、点列の収束への言い換え
距離空間の間の写像の収束の、点列の収束への言い換え |
|
定理 1 |
次の命題 P,Q,Rは互いに言い換え可能である。
つまり、命題P⇔命題Q⇔命題R。
命題P:
点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
関数f (P) = f (x1,x2,…,xn)が実数cに収束する
これを記号で表すと、
・f ( P )→c ( P → A )
・f (x1,x2,…,xn)→c ( x1→a1 , x2→a2 ,…,xn→an )
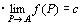
など。 |
[ 文献]
吹田・新保『理工系の微分積分学』p. 159.
杉浦『解析入門I』定理6.2(p.53):証明付;
髙木『解析概論』9極限(p.22):証明付. |
|
命題 Q:
どんなRn上の点列{ Pi }={ P1 , P2 , P3,…}={ (x11,x12,…,x1n) , (x21,x22,…,x2n) , (x31,x32,…,x3n) ,…}についてであれ、
1. その点列{ Pi }={ P1 , P2 , P3,…}={ (x11,x12,…,x1n) , (x21,x22,…,x2n) , (x31,x32,…,x3n) ,…}が点A(a1,a2,…,an)に収束し、
かつ
2. その点列の各項 P1 , P2 , P3 , … がどれも点Aと一致しない
限り、
その点列の各項 P1 , P2 , P3 , …を n変数関数f によりR上に写した像の数列
{ f ( Pi ) }={ f ( P1 ), f ( P2 ) , f ( P3 ) ,… }={ f ( x11,x12,…,x1n ) , f (x21,x22,…,x2n ), f (x31,x32,…,x3n ),… }
は実数cに収束する。
つまり、
任意のRn上の点列{ PI }={ P1 , P2 , P3,…}={ (x11,x12,…,x1n) , (x21,x22,…,x2n) , (x31,x32,…,x3n) ,…}について、
Pi→A (i→∞) かつ P1≠A , P2≠A , P3≠A ,…ならば、f (Pi)→c (i→∞)
論理記号で表すと、
(∀{ Pi })(( Pi→A (i→∞)かつ(∀i) ( Pi ≠A) )⇒ f (Pi)→c (i→∞))
命題 R:
いかなる
「実数a1に収束する数列{ x11 , x21 , x31 ,…}」(ただし、x11≠a1 , x21≠a1 , x31≠a1 ,… )
「実数a2に収束する数列{ x12 , x22 , x32 ,…}」(ただし、x12≠a2 , x22≠a2 , x32≠a2 ,… )
:
「実数anに収束する数列{ x1n , x2n , x3n ,…}」(ただし、x1n ≠an , x2n ≠an , x3n ≠an ,… )
に対しても、
数列
{ f ( Pi ) }={ f ( P1 ), f ( P2 ) , f ( P3 ) ,… }={ f ( x11,x12,…,x1n ) , f (x21,x22,…,x2n ), f (x31,x32,…,x3n ),… }
が実数cに収束する。
つまり、
(∀ { xi1 } ,{ xi2 }, …, { xin } )
(((∀i) (xi1≠a1かつxi2≠a2かつ…かつxin≠an)かつxi1→a1 (i→∞)かつxi2→a2 (i→∞)かつ…かつxin→an (i→∞))
⇒ f ( xi1,xi2,…,xin )→c (i→∞))
※なぜ?
・「命題P⇒命題Q」となるわけ→証明 [杉浦『解析入門I』定理6.2(p.53)]
・「命題Q⇒命題P」となるわけ→証明 [杉浦『解析入門I』定理6.2(p.53);髙木『解析概論』p.22;]
・「命題Q⇔命題R」となるのは、点列の収束と数列の収束の関係による。 |
|
定理 2 |
次の命題 P,Q,Rは互いに言い換え可能である。
つまり、命題P⇔命題Q⇔命題R。
命題P:
点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
関数f (P) = f (x1,x2,…,xn)が収束する。
すなわち、
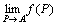 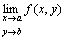
が存在する
※極限値の値をだしていないことに注意。 |
[ 文献]
小平『解析入門Ⅱ』p.259:証明略;
杉浦『解析入門I』定理6.2系(p.54):証明付 |
|
命題 Q:
どんなRn上の点列{ Pi }={ P1 , P2 , P3,…}={ (x11,x12,…,x1n) , (x21,x22,…,x2n) , (x31,x32,…,x3n) ,…}についてであれ、
1. その点列{ Pi }={ P1 , P2 , P3,…}={ (x11,x12,…,x1n) , (x21,x22,…,x2n) , (x31,x32,…,x3n) ,…}が点A(a1,a2,…,an)に収束し、
かつ
2. その点列の各項 P1 , P2 , P3 , … がどれも点Aと一致しない
限り、
その点列の各項 P1 , P2 , P3 , …を n変数関数f によりR上に写した像の数列
{ f ( Pi ) }={ f ( P1 ), f ( P2 ) , f ( P3 ) ,… }={ f ( x11,x12,…,x1n ) , f (x21,x22,…,x2n ), f (x31,x32,…,x3n ),… }
が収束する。
論理記号で表すと、
(∀{ Pi })(( Pi→A (i→∞)かつ(∀i) ( Pi ≠A) )⇒ 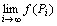 ) )
※極限値の値をだしていないことに注意。
命題 R:
いかなる
「収束数列{ x11 , x21 , x31 ,…}」(ただし、x11≠a1 , x21≠a1 , x31≠a1 ,… )
「収束数列{ x12 , x22 , x32 ,…}」(ただし、x12≠a2 , x22≠a2 , x32≠a2 ,… )
:
「収束数列{ x1n , x2n , x3n ,…}」(ただし、x1n ≠an , x2n ≠an , x3n ≠an ,… )
に対しても、
数列
{ f ( Pi ) }={ f ( P1 ), f ( P2 ) , f ( P3 ) ,… }={ f ( x11,x12,…,x1n ) , f (x21,x22,…,x2n ), f (x31,x32,…,x3n ),… }
が収束する。 |
|
活用例 |
コーシーの判定条件 |
|
→[トピック一覧:n変数関数の極限]
→総目次
|
|
|
定義:∞に発散する |
| |
cf .1変数関数の発散/ 2変数関数の発散 |
|
はじめに
読むべき
定義 |
「 点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
関数f (P) = f (x1,x2,…,xn)が∞に発散する」
f ( x1,x2,…,xn )→+∞ ( x1→a1 , x2→a2 , xn→an ) f ( P )→+∞ ( P → A )
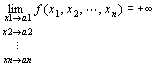 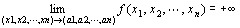
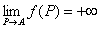
とは、
点P(x1,x2,…,xn)を、
点A(a1,a2,…,an)に一致させることなく点A(a1,a2,…,an)に近づけるとき、
関数f (P) = f (x1,x2,…,xn) が限りなく大きくなることをいう。
※この定義は一見わかりやすい。
ところが、
「近づく」「限りなく大きくなる」とはいかなる事態を指すのかという点が、
明らかにされておらず、
この「発散」定義は不正確で、証明のなかでは使いものにならない。
そこで、
「近づく」「限りなく大きくなる」の意味を明確化するために、
「発散」概念は、次のように厳密化される。 |
[ 文献]
高木・押切
『解析I・微分』p.25.
杉浦
『解析入門I』I§6定義8(p.60);
|
|
厳密な
定義 |
「 点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、関数f (P) = f (x1,x2,…,xn)が∞に発散する」
f ( x1,x2,…,xn )→+∞ ( x1→a1 , x2→a2 , xn→an ) f ( P )→+∞ ( P → A )
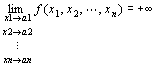 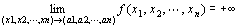
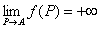
とは、
任意の(どんな大きな)実数Kに対して(でも)、ある正の実数δをとると、
「0<d( P, A )<δ ならば f (P) = f (x1,x2,…,xn)>K 」
が成りたつ
ということ。
この定義を、論理記号で表せば、
(∀K∈R)(∃δ>0)(0<d( P, A )<δ⇒f (P) = f (x1,x2,…,xn)>K )
となる。
* d( P, A )は、 n次元空間Rn上での点P(x1,x2,…,xn)と点A(a1,a2,…,an)との距離を表す。 |
|
Euclid 平面
において |
関数f (P) = f (x1,x2,…,xn)、すなわち、「 n次元空間Rnの部分集合から、実数体Rへの、写像」について、
収束・極限・発散等を扱う際には、
特別な目的がない限り、
n次元空間Rn上の距離をユークリッド距離で定めて、 n次元空間Rnをユークリッド空間Rnとする
設定のもとで考えるのが普通。
この設定下では、
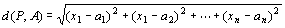
だから、
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、関数f (P) = f (x1,x2,…,xn)が∞に発散する」
の定義は、具体的には
┌任意の(どんな大きな)実数Kに対して(でも)、
|ある正の実数δをとると、
| 「 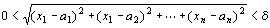
| ならば f (x1,x2,…,xn) >K 」
└を成り立たせる
(∀K∈R)(∃δ>0)(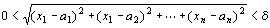 ⇒ f (x1,x2,…,xn) > K ) ⇒ f (x1,x2,…,xn) > K )
となる。 |
|
数ベクトル空間
の上に
定義された
Euclid平面
において |
Rn にベクトルの加法・スカラー乗法・自然な内積(標準内積)・ユークリッドノルム∥∥が定義されており、
Rn を実n次元数ベクトル空間・計量実ベクトル空間・ノルム空間として扱える場合、
任意の実n次元数ベクトルx, y∈Rn のユークリッド距離は∥x-y∥ と表せる。
このユークリッド距離を定義したユークリッド平面Rnのもとでは、
d( P, A )=∥P-A∥
だから、
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、関数f (P) = f (x1,x2,…,xn)が∞に発散する」の定義は、
┌任意の(どんな大きな)実数Kに対して(でも)、
|ある正の実数δが存在して、
| 「 0<∥P-A∥<δ ならば f (x1,x2,…,xn) >K 」
└を成り立たせる
(∀K∈R)(∃δ>0)(0<∥P-A∥<δ⇒f (x1,x2,…,xn) >K )
と表せる。
ただし、上記のPは、「点P(x1,x2,…,xn)」を表す実n次元数ベクトル(x1,x2,…,xn)、
上記のAは、「点A(a1,a2,…,an)」を表す実n次元数ベクトル(a1,a2,…,an)
である。 |
|
|
|
|
→ [トピック一覧:n変数関数の極限]
→総目次
|
|
|
定義:-∞に発散する |
| |
cf .1変数関数の発散/ 2変数関数の発散 |
|
|
はじめに
読むべき
定義 |
「 点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
関数f (P) = f (x1,x2,…,xn)が-∞に発散する」
f ( x1,x2,…,xn )→-∞ ( x1→a1 , x2→a2 , xn→an ) f ( P )→-∞ ( P → A )
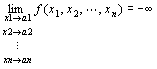 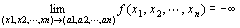
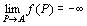
とは、
点P(x1,x2,…,xn)を、
点A(a1,a2,…,an)に一致させることなく点A(a1,a2,…,an)に近づけるとき、
関数f (P) = f (x1,x2,…,xn) が限りなく小さくなることをいう。
※この定義は一見わかりやすい。
ところが、
「近づく」「限りなく小さくなる」とはいかなる事態を指すのかという点が、
明らかにされておらず、
この「発散」定義は不正確で、証明のなかでは使いものにならない。
そこで、
「近づく」「限りなく小さくなる」の意味を明確化するために、
「発散」概念は、次のように厳密化される。 |
[ 文献]
杉浦
『解析入門I』I§6定義8(p.60);高木・押切
『解析I・微分』p.25. |
|
厳密な
定義 |
「 点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、関数f (P) = f (x1,x2,…,xn)が-∞に発散する」
f ( x1,x2,…,xn )→-∞ ( x1→a1 , x2→a2 , xn→an ) f ( P )→-∞ ( P → A )
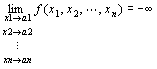 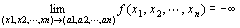
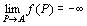
とは、
任意の(どんな小さな)実数Kに対して(でも)、ある正の実数δをとると、
「0<d( P, A )<δ ならば f (x1,x2,…,xn)<K 」
が成りたつ
ということ。
この定義を、論理記号で表せば、
(∀K∈R)(∃δ>0)(0<d( P, A )<δ⇒f (x1,x2,…,xn)<K )
となる。
* d( P, A )は、 n次元空間Rn上での点P(x1,x2,…,xn)と点A(a1,a2,…,an)との距離を表す。 |
|
Euclid 平面
において |
関数f (P) = f (x1,x2,…,xn)、すなわち、「 n次元空間Rnの部分集合から、実数体Rへの、写像」について、
収束・極限・発散等を扱う際には、
特別な目的がない限り、
n次元空間Rn上の距離をユークリッド距離で定めて、 n次元空間Rnをユークリッド空間Rnとする
設定のもとで考えるのが普通。
この設定下では、
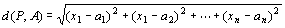
だから、
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、関数f (P) = f (x1,x2,…,xn)が∞に発散する」
の定義は、具体的には
┌任意の(どんな小さな)実数Kに対して(でも)、
|ある正の実数δをとると、
| 「 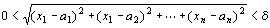
| ならば f (x1,x2,…,xn) <K 」
└を成り立たせる
(∀K∈R)(∃δ>0)(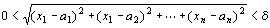 ⇒ f (x1,x2,…,xn) < K ) ⇒ f (x1,x2,…,xn) < K )
となる。 |
|
数ベクトル空間
の上に
定義された
Euclid平面
において |
Rn にベクトルの加法・スカラー乗法・自然な内積(標準内積)・ユークリッドノルム∥∥が定義されており、
Rn を実n次元数ベクトル空間・計量実ベクトル空間・ノルム空間として扱える場合、
任意の実n次元数ベクトルx, y∈Rn のユークリッド距離は∥x-y∥ と表せる。
このユークリッド距離を定義したユークリッド平面Rnのもとでは、
d( P, A )=∥P-A∥
だから、
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、関数f (P) = f (x1,x2,…,xn)が-∞に発散する」の定義は、
┌任意の(どんな小さな)実数Kに対して(でも)、
|ある正の実数δが存在して、
| 「 0<∥P-A∥<δ ならば f (x1,x2,…,xn) <K 」
└を成り立たせる
(∀K∈R)(∃δ>0)(0<∥P-A∥<δ⇒f (x1,x2,…,xn) <K )
と表せる。
ただし、上記のPは、「点P(x1,x2,…,xn)」を表す実n次元数ベクトル(x1,x2,…,xn)、
上記のAは、「点A(a1,a2,…,an)」を表す実n次元数ベクトル(a1,a2,…,an)
である。 |
|
|
|