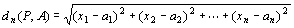|
|
|
|
定義:ベクトル値関数が点 Aで連続 |
|
はじめに
読むべき
定義 |
「 ベクトル値関数 ( y1 ,y2 , …, ym )=f ( x1 , x2 , … , xn )は、
点( a1 , a2 , … , an )で連続continuousである」
とは、
次の3条件がすべて満たされることを言う。
(1) f (a1,a2,…,an) が定義されていること
(2) ( x1 , x2 , … , xn ) → ( a1 , a2 , … , an )で、
f (x1 , x2 , … , xn)が収束すること。
つまり、
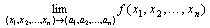
が存在すること。
(3) ( x1 , x2 , … , xn ) → ( a1 , a2 , … , an )で、
f (x1 , x2 , … , xn)→ f (a1 , a2 , … , an)
となること。
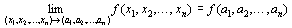
が成立すること。
※上記条件の一つでも満たされていないとき、
f は点Aで不連続であるdiscontinuous、
ないしは、f は点A(a1,a2,…,an)で不連続であるという。 |
cf.点集合上連続/一様連続性
[ 具体例]1変数関数の連続性/2変数関数の連続性/多変数関数の連続性
[ 一般化]距離空間上の写像/位相空間上の写像
[ 文献]
杉浦『解析入門I』定義5(p.55-56);
斉藤『数学の基礎:集合・数・位相』3.4.16 (p.90);
髙木『解析概論』10連続函数(p.26)
|
|
設定 |
厳密には、「 ベクトル値関数 f は点Aで連続」の定義は、
以下の手順で設定された舞台上でなされる。
Step1: n次元空間Rn 、m次元空間Rmを用意する。
* n次元空間Rnとは、
実数をn個並べた組 (x1,x2,…,xn ) をすべてあつめた集合。
実n次元数ベクトルをすべて集めた集合でもある。
* m次元空間Rmとは、
実数をm個並べた組 (y1,y2,…,ym ) をすべてあつめた集合。
実m次元数ベクトルをすべて集めた集合でもある。 |
|
Step 2: n次元空間Rnに距離dnを定めて、距離空間(Rn,dn)を設定。
*普通は、 n次元空間Rnにユークリッド距離を与えたユークリッド空間を考える。
m次元空間Rmに距離dmを定めて、距離空間(Rm,dm)を設定。
*普通は、 m次元空間Rmにユークリッド距離を与えたユークリッド空間を考える。
Step3: n次元空間Rn上の点集合のひとつを選んで集合Dと名づける。
つまり、「D⊂Rn」
*Dは、「実n次元数ベクトルの集合」でもある。
Step4: n次元空間Rnの点集合D上の各点Pにたいして m次元空間Rm上の点を対応づけるベクトル値関数f
を用意。
つまり、
f : D→Rm (D⊂Rn ) ないし ( f1 (x1,x2,…,xn), f2 (x1,x2,…,xn) ,…, fm (x1,x2,…,xn))= f (x1,x2,…,xn)
*fはそれぞれ「Dに属す各実n次元数ベクトルから実m次元数ベクトルへの対応付け」だとも言える。 |
|
Step 5:「 n次元空間Rnの点集合D」に属す動点を、P= (x1,x2,…,xn )と名づける。
つまり、「P∈D⊂Rn」
*Pは、「Dに属す実n次元数ベクトル」でもある。
Step 6:「 n次元空間Rnの点集合D」に属すある定点を、A=(a1,a2,…,an)で表す。
つまり、A=(a1,a2,…,an)∈D⊂Rn
*Aは、「Dに属す実n次元数ベクトル」でもある。 |
[ 文献]
杉浦『解析入門I』命題6.5-b(p.55-56);
黒田『微分積分学』8.2.3(p.278);
松坂『集合・位相入門』4章§1-G(p.149);
斉藤『数学の基礎:集合・数・位相』3.4.16 (p.90);
入谷久我『数理経済学入門』補助定理5.5(p.122);
ルディン『現代解析学』4.5(p.83):一般の距離空間上で。
布川谷野中山『線形代数と凸解析』定義6.8(p.123):ノルムを使って。
|
|
厳密な
定義
ε -δ論法 |
「 ベクトル値関数 f は、点Aで連続であるcontinuous」とは、
任意の正数εに対して、ある正の実数δが存在して、
任意の点Pに対し「 dn( P, A )<δ ならば dm( f (P), f (A) )<ε 」
を成り立たせる、ということ。
この定義を、論理記号で表せば、
(∀ε>0)(∃δ>0)(∀P∈Rn)( dn( P, A )<δ⇒ dm ( f (P), f (A) )<ε)
* dn( P, A )は、 n次元空間Rn上での点Pと点Aとの距離を、
dm ( f (P), f (A) )は、 m次元空間Rm上のf (P)と f (A) との距離を表す。
* 「P→Aのときf(P)が収束する」の定義では、 0<dn( P, A )<δ であった。
つまり、関数の「極限」では、P=Aを除外して考えたが、
「連続」ではP=Aを除外しないことになる。 |
|
※ユークリッド距離が定められたユークリッド空間 Rn,Rmにおける連続概念
ベクトル値関数(f1 (x1,x2,…,xn),f2 (x1,x2,…,xn),…,fm (x1,x2,…,xn)) = f (x1,x2,…,xn)について、
すなわち「『 n次元空間Rnの部分集合』から『 m次元空間Rm』への写像」を扱う際には、
特別な目的がない限り、
n次元空間Rn上の距離をn次元ユークリッド距離で定めて、 n次元空間Rnをユークリッド空間Rnとし、
m次元空間Rm上の距離をm次元ユークリッド距離で定めて、 m次元空間Rmをユークリッド空間Rmとする
設定のもとで
考えるのが普通。
この設定下では、
Rn上の点P= (x1,x2,…,xn )と、点A=(a1,a2,…,an)に対して、
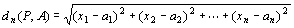
Rm上の点 f (P)=f (x1,x2,…,xn )=(f1 (x1,x2,…,xn),f2 (x1,x2,…,xn),…,fm (x1,x2,…,xn ) ) と、
点 f (A)=f (a1,a2,…,an )=(f1 (a1,a2,…,an),f2 (a1,a2,…,an ),…,fm (a1,a2,…,an ))
に対して、
dm ( f (P), f (A) )
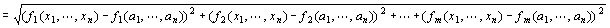
だから、
「ベクトル値関数(f1 (x1,x2,…,xn),f2 (x1,x2,…,xn),…,fm (x1,x2,…,xn)) = f (x1,x2,…,xn)は、
点A=(a1,a2,…,an)で連続である」の定義は、
具体的には
┌任意の(どんな)正の実数εに対して(でも)、ある正の実数δが存在して、
| 「 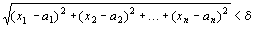
| ならば
| 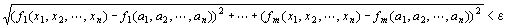 」 」
└を成り立たせる
(∀ε>0)(∃δ>0)(∀x1,x2,…,xn ∈R )
(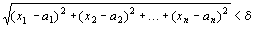
⇒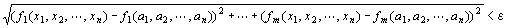 ) )
となる。 |
|
※ n次元数ベクトル空間,m次元数ベクトル空間の上に定義されたユークリッド空間Rn,Rmにおける連続概念
・ n次元空間Rnに
ベクトルの加法・スカラー乗法・自然な内積(標準内積)・ユークリッドノルム∥∥nが定義されており、
n次元空間Rnを実n次元数ベクトル空間・計量実ベクトル空間・ノルム空間として扱える場合、
任意の実n次元数ベクトルx, y∈Rnのユークリッド距離は∥x-y∥n と表せる。
このユークリッド距離を定義したユークリッド空間Rnのもとでは、
dn( P, A )=∥P-A∥n
・ m次元空間Rmに
ベクトルの加法・スカラー乗法・自然な内積(標準内積)・ユークリッドノルム∥∥mが定義されており、
m次元空間Rmを実n次元数ベクトル空間・計量実ベクトル空間・ノルム空間として扱える場合、
任意の実m次元数ベクトルx', y'∈Rmのユークリッド距離は∥x-y∥m と表せる。
このユークリッド距離を定義したユークリッド空間Rmのもとでは、
dm( f (P), f (A) )=∥f (P)-f (A)∥m
・したがって、
「ベクトル値関数 f (P) は、点Aで連続である」の定義は、
「任意の(どんな)正の実数εに対して(でも)、ある正の実数δが存在して、
『 ∥P-A∥n<δ ならば ∥f (P)-f (A)∥m <ε』
を成り立たせる」
(∀ε>0)(∃δ>0)(∀P∈Rn)(∥P-A∥n<δ⇒∥f (P)-f (A)∥m<ε )
と表せる。
ただし、上記のPは、「点P(x1,x2,…,xn )」を表す実n次元数ベクトル (x1,x2,…,xn ) 、
上記のAは、「点A(a1,a2,…,an)」を表す実n次元数ベクトル (a1,a2,…,an)
である。 |
|
厳密な
定義
近傍 |
「 ベクトル値関数 f は点Aで連続であるcontinuous」とは、
点f (A)の任意の「Rm上のε近傍 Uε(f (A))」に対して(でも)、
ある「Rn上の点Aのδ近傍Uδ(A)」が存在して、
f ( Uδ(A) ) ⊂ Uε(f (A))
を満たす
ということ。
この定義を別の表現でいうと、
任意の(どんな)正の実数εに対して(でも)、ある正の実数δが存在して、
「 f ( Uδ(A) ) ⊂ Uε(f (A)) 」
すなわち「 P∈Uδ(A) ならば、f (P) ∈Uε(f (A)) 」
を成り立たせる、
ということ。
この定義を、論理記号で表せば、
(∀ε>0)(∃δ>0)( f ( Uδ(A) ) ⊂ Uε(f (A)) )
(∀ε>0)(∃δ>0)(∀P∈Rn)( P∈Uδ(A) ⇒ f (P) ∈Uε(f (A)))
となる。 |
[ 文献]
杉浦『解析入門I』命題6.5-c(p.55-56);
松坂『集合・位相入門』4章§1-G(p.149);
斉藤『数学の基礎:集合・数・位相』3.4.16 (p.90)
|
|
活用例 |
|
|
|
|
|
|
→ [トピック一覧:ベクトル値関数の連続性]
→総目次
|
|
|
定義:ベクトル値関数が点集合 D上で連続 |
|
はじめに
読むべき
定義 |
「 ベクトル値関数 ( y1 ,y2 , …, ym )=f ( x1 , x2 , … , xn ) は
点集合D上で連続continuousである」
とは、
ベクトル値関数( y1 ,y2 , …, ym )=f ( x1 , x2 , … , xn )が
点集合Dに属す各点で連続であること
をいう。 |
Cf.点での連続性/一様連続性
[具体例]1変数関数の区間連続性/2変数関数が集合上連続/ n変数関数が集合上連続
[ 一般化]実数値関数/距離空間上の写像/位相空間上の写像
[ 文献]
杉浦『解析入門I』I章§6定義5(p.55);Ⅳ章§4定義1(4.2):一様連続との比較。
黒田『微分積分学』8.2.3(p.278);
斉藤『数学の基礎:集合・数・位相』3.4.16 (p.90); |
|
設定 |
厳密には、「 ベクトル値関数 f は点Aで連続」の定義は、
以下の手順で設定された舞台上でなされる。
Step1: n次元空間Rn 、m次元空間Rmを用意する。
* n次元空間Rnとは、
実数をn個並べた組 (x1,x2,…,xn ) をすべてあつめた集合。
実n次元数ベクトルをすべて集めた集合でもある。
* m次元空間Rmとは、
実数をm個並べた組 (y1,y2,…,ym ) をすべてあつめた集合。
実m次元数ベクトルをすべて集めた集合でもある。 |
| |
Step 2: n次元空間Rnに距離dnを定めて、距離空間(Rn,dn)を設定。
*普通は、 n次元空間Rnにユークリッド距離を与えたユークリッド空間を考える。
m次元空間Rmに距離dmを定めて、距離空間(Rm,dm)を設定。
*普通は、 m次元空間Rmにユークリッド距離を与えたユークリッド空間を考える。
Step3: n次元空間Rn上の点集合のひとつを選んで集合Dと名づける。
つまり、「D⊂Rn」
*Dは、「実n次元数ベクトルの集合」でもある。
Step4: n次元空間Rnの点集合D上の各点Pにたいして m次元空間Rm上の点を対応づけるベクトル値関数f
を用意。
つまり、
f : D→Rm (D⊂Rn ) ないし ( f1 (x1,x2,…,xn), f2 (x1,x2,…,xn) ,…, fm (x1,x2,…,xn))= f (x1,x2,…,xn)
*fはそれぞれ「Dに属す各実n次元数ベクトルから実m次元数ベクトルへの対応付け」だとも言える。 |
|
厳密な
定義
ε -δ論法 |
「 ベクトル値関数 f は、点集合D上で連続であるcontinuous」とは、
点集合Dに属す点Aをひとつ選んで固定した上で、
任意の正数εに対して、ある正数δをとると、
任意の点Pに対し「 dn( P, A )<δ ならば dm( f (P), f (A) )<ε 」 …(1)
が成り立ち、
これが、すべての点A∈Dについてもいえるということ。
この定義を、論理記号で表せば、
( ∀ A∈D )(∀ε>0)(∃δ>0)(∀P∈D)( dn( P, A )<δ⇒ dm ( f (P), f (A) )<ε)
* dn( P, A )は、 n次元空間Rn上での点Pと点Aとの距離を、
dm ( f (P), f (A) )は、 m次元空間Rm上のf (P)と f (A) との距離を表す。
※ここで、(1)を満たすδを全てのA∈Dに対して共通に選ぶ必要はないことに注意。
「f(P)がD上で連続」と言った場合、A∈Dの選び方で(1)を満たすδが変わってもよい。
これに対して、
(1)を満たすδを全てのA∈Dに対して共通に選べる、
A∈Dの選び方によらず、εだけに対応して (1)を満たすδを一様に選べることを意味する概念は、
一様連続性。 |
| |
|
|
定理:「ベクトル値関数についての連続性」の「 n変数関数の連続性」への言い換え |
| |
次の命題 Pと命題Qは互いに言い換え可能である。
つまり、命題P⇔命題Q。
命題 P:ベクトル値関数 ( y1 ,y2 , …, ym )=f ( x1 , x2 , … , xn )は、
点( a1 , a2 , … , an )で連続。
命題 Q:ベクトル値関数 ( y1 ,y2 , …, ym )=f ( x1 , x2 , … , xn )を、
m個の n変数関数の組
y1 = f1 ( x1 , x2 , … , xn )
y2 = f2 ( x1 , x2 , … , xn )
:
ym =fm ( x1 , x2 , … , xn )
として表したときに、
f1 , f2 , … , fm は、どれも点( a1 , a2 , … , an )で連続。
すなわち、
y1 = f1 ( x1 , x2 , … , xn ) は、点( a1 , a2 , … , an )で連続。
かつ
y2 = f2 ( x1 , x2 , … , xn ) は、点( a1 , a2 , … , an )で連続。
かつ
:
かつ
ym =fm ( x1 , x2 , … , xn ) は、点( a1 , a2 , … , an )で連続。
※ なぜ?
「ベクトル値関数の極限」の「n変数関数の極限」への言い換えによる。
|
[文献]
杉浦『解析入門I』I章§6定理6.8-2(p.60);
ルディン『現代解析学』4.5(p.83):距離空間上で定義されたベクトル値関数について。
黒田『微分積分学』8.2.3(p.278);
入谷久我『数理経済学入門』定義5.7(p.122);
西村『経済数学早分かり』3章§1.2連続関数(p.107);
|
| |
|
|
|
定理:ベクトル値関数の点における連続性の、点列の収束への言い換え |
| |
具体例: 1変数関数の連続の、数列の収束への言い換え / 2変数関数の連続の、点列・数列の収束への言い換え
n変数関数の連続の、点列・数列の収束への言い換え
一般化: 距離空間の間の写像の連続の、点列の収束への言い換え |
|
定理 1 |
次の命題 P,命題Qは互いに言い換え可能である。
つまり、命題P⇔命題Q。
命題 P:
ベクトル値関数
( y1 ,y2 , …, ym )=f ( x1 , x2 , … , xn )
は、
点A( a1 , a2 , … , an )で連続。 |
[ 文献]
入谷久我『数理経済学入門』補助定理5.4(p.122);
加古『自然科学の基礎としての微積分』定義6.1(p.91);
西村『経済数学早分かり』3章§1.2連続関数(p.107);
|
|
命題 Q:
どんなRn上の点列{ Pn }={ P1 , P2 , P3,…}={ (x11,x12,…,x1n), (x21,x22,…,x2n) , (x31,x32,…,x3n) ,…}についてであれ、
その点列{ Pn }={ P1 , P2 , P3,…}={ (x11,x12,…,x1n), (x21,x22,…,x2n) , (x31,x32,…,x3n) ,…}が
点A( a1 , a2 , … , an )に収束する限り、
その点列の各項 P1 , P2 , P3,…をベクトル値関数f によりRm上に写した像の点列
{ f ( Pn ) }={ f ( P1 ) , f ( P2 ) , f ( P3 ) ,… }={ f ( x11,x12,…,x1n ) , f ( x21,x22,…,x2n ), f ( x31,x32,…,x3n ),… }
は、
点A( a1 , a2 , … , an )をベクトル値関数f によりRm上に写した像
f ( A )=f ( a1 , a2 , … , an )
に収束する。
つまり、
任意のRn上の点列{ Pn }={ P1 , P2 , P3,…}について、
Pn→A (n→∞) ならば、f (Pn) →f ( A ) (n→∞)
論理記号で表すと、
(∀{ Pn })(( Pn→A (n→∞) )⇒( f (Pn) →f ( A ) (n→∞)))
※なぜ?
関数の収束の定義と、関数の連続性の定義を見比べたうえで、
関数の収束と点列の収束の関連性についての定理を、関数の連続性向けに修正。 |
|
活用例 |
|
|
|
定義:ベクトル値関数の一様連続性 uniformly continuous |
|
設定 |
「 ベクトル値関数の一様連続性」の定義は、
以下の手順で設定された舞台上でなされる。
Step1: n次元空間Rn 、m次元空間Rmを用意する。
* n次元空間Rnとは、
実数をn個並べた組 (x1,x2,…,xn ) をすべてあつめた集合。
実n次元数ベクトルをすべて集めた集合でもある。
* m次元空間Rmとは、
実数をm個並べた組 (y1,y2,…,ym ) をすべてあつめた集合。
実m次元数ベクトルをすべて集めた集合でもある。
Step2-1: n次元空間Rnに距離dnを定めて、距離空間(Rn,dn)を設定。
*普通は、 n次元空間Rnにユークリッド距離を与えた
ユークリッド空間を考える。
Step2-2: m次元空間Rmに距離dmを定めて、距離空間(Rm,dm)を設定。
*普通は、 m次元空間Rmにユークリッド距離を与えた
ユークリッド空間を考える。
Step3: n次元空間Rn上の点集合のひとつを選んで集合Dと名づける。
つまり、「D⊂Rn」
*Dは、「実n次元数ベクトルの集合」でもある。
Step4: n次元空間Rnの点集合D上の各点Pにたいして
m次元空間Rm上の点を対応づける
ベクトル値関数fを用意。
つまり、
f : D→Rm (D⊂Rn )
ないし
( f1 (x1,x2,…,xn), f2 (x1,x2,…,xn) ,…, fm (x1,x2,…,xn))= f (x1,x2,…,xn)
*fは
「Dに属す各実n次元数ベクトルから
実m次元数ベクトルへの対応付け」だとも言える。
Step5:「 n次元空間Rnの点集合D」に属す2点を、
P= (x1,x2,…,xn )、A = (a1,a2,…,an )と名づける。
つまり、「P, A∈D⊂Rn」
*P, Aは、「Dに属す実n次元数ベクトル」といってもよい。 |
cf.D上で連続:δが各A∈D毎にちがっていてもよい。
cf .点での連続性
[具体例]1変数関数の一様連続性/2変数関数の一様連続性/ n変数関数の一様連続性
[一般化]実数値関数の一様連続性/距離空間のあいだの写像の一様連続性
[ 文献]
斉藤『数学の基礎:集合・数・位相』3.4.17 (p.90)
杉浦『解析入門I』Ⅳ章積分§4連続関数の可積分性-定義1(p. 225).;
ルディン『現代解析学』4.18(p.88):距離空間一般上。
|
|
定義 |
ベクトル値関数f (P)=f (x1,x2,…,xn)が、点集合D上で一様連続uniformly continuousであるとは、
任意の正数εに対して、ある正数δが存在して、
「dn (P, A)<δを満たす限りで任意の『Dの元』」P,Aについて、dm ( f (P) , f (A) )<εが成り立つ
ということ。
論理記号で表せば、すなわち、
( ∀ε>0 ) ( ∃δ>0 ) ( ∀ A∈D ) ( ∀ P ∈D ) ( dn ( P, A )<δ ⇒ dm ( f (P) , f (A) )<ε)
※δが、各A∈Dに対して一様にとれることを意味している点が、重要。 |
|
性質 |
・ ベクトル値関数f が点集合D上で一様連続ならば、f は点集合D上で連続。
・一般には、ベクトル値関数f が点集合D上で連続だからといって、点集合D上で一様連続だとは限らない。
・点集合Dが有界な閉集合ならば、ベクトル値関数f が点集合Dで一様連続であることと連続であることは同値
→詳細 |
|
否定命題 |
「 ベクトル値関数f (P)=f (x1,x2,…,xn)が、点集合D上で一様連続でない」とは、
( ∃ε>0 ) ( ∀δ>0 ) ( ∃A∈D ) ( ∃ P ∈D ) ( dn (P, A)<δかつ dm ( f (P) , f (A) )≧ε)
[杉浦『解析入門I』Ⅳ章積分§4連続関数の可積分性-定理4.1証明(4.4)(p. 226)] |
| |
|
| |
|
|