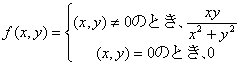2変数関数の連続性：トピック一覧　　

　・連続性の定義：点での連続性/右連続/左連続/点集合上連続/連続関数/一様連続性　
　・2変数についての連続性の性質：各変数についての連続性との関係/点列の収束との関係　
　・連続関数一般の性質：関数の和差積商の連続性/合成関数の連続性　
　・有界閉集合上の性質：連続関数による有界閉集合の像は有界閉集合/有界閉集合上連続な関数は有界/最大値最小値定理/
　　　　　　　　　　　　関数f (x)を有界閉集合D上で連続とすると、fはDにおいて一様連続
　・連結な集合上の性質：中間値定理/連続関数による領域の像は区間/連続関数による閉領域の像は閉区間　　

※2変数関数以外の関数の連続性：1変数関数の連続性/ n変数関数の連続性/ベクトル値関数の連続性
※2変数関数の連続性の一般化：実数値関数の連続性/距離空間のあいだの連続写像/位相空間のあいだの連続写像　
※2変数関数に関する他の概念：2変数関数の諸属性/極限/極限の性質/偏微分/全微分/矩形上の積分/点集合上の積分

※参考文献/総目次

定義：2変数関数が点Aで連続

はじめに
読むべき
定義

「f (P)すなわちf (x,y)は、点A(a,b)で連続であるcontinuous」
とは、
次の3条件がすべて満たされることを言う。
(1)　　f (A)、すなわち、f (a,b)　が定義されていること
(2)
　　　
　　　が存在すること。　
　　　つまり、P→Aで、f (P)が収束すること。　　　
(3)
　　　
　　　が成立すること。
　　　つまり、f (P)→f (A)（P→A）　　　
※上記条件の一つでも満たされていないとき、
　f (P)は点Aで不連続であるdiscontinuous、
　ないしは、f (x,y)は点(a,b)で不連続であるという。

cf.点集合上連続/一様連続性

類概念：1変数関数の連続性

連続性の一般化： n変数関数/実数値関数/ベクトル値関数の連続性/距離空間上の写像/位相空間上の写像

[文献]
和達『微分積分』pp.115-6;
吹田新保『理工系の微分積分学』p.160
杉浦『解析入門I』定義5(p.55-56);
��木『解析概論』10連続函数(p.26)

舞台設定

厳密には、「2変数関数が点Aで連続」の定義は、以下の手順で設定された舞台上でなされる。　
Step1：平面R²を用意する。
　　　　*R²とは、実数を2個並べた組 (x,y ) をすべてあつめた集合。
　　　　　実2次元数ベクトルをすべて集めた集合でもある。
Step2：平面R²に距離dを定めて、距離空間(R²,d)を設定。
　　　　*普通は、平面R²にユークリッド距離を与えて、ユークリッド平面を考える。　
Step3：平面R²上の点集合のひとつを選んで、集合Dと名づける。つまり、「D⊂R²」　
　　　　*Dは、「実2次元数ベクトルの集合」とも呼べる。　
Step4：平面R²上の点集合Dで定義された2変数関数 f を用意。
　　　　つまり、f : D→R　（D⊂R² ）　,　z=f(P) ( z∈R, P∈D⊂R² ) 　,　z=f(x,y) ( z∈R, (x, y)∈D⊂R² )　
　　　　*fは「Dに属す各実2次元数ベクトルから実数への対応付け」だとも言える。
Step5：「平面R²上の点集合D」に属す動点を、P=(x, y)と名づける。　
　　　「平面R²上の点集合D」に属す定点を、A = (a,b)と名づける。　
　　　　　　　　つまり、「P, A∈D⊂R²」　　
　　　　*P, Aは、「Dに属す実2次元数ベクトル」といってもよい。

厳密な
定義
ε-δ論法

「f (P)=f (x,y)は、点A(a,b)で連続であるcontinuous」とは、
　任意の正数εに対して、ある正の実数δが存在して、
　　「 d ( P, A )＜δ ならば、d ( f (P), f (A) )＜ε 」　
　を成り立たせる、ということ。
この定義を、論理記号で表せば、
（∀ε>０）（∃δ>０）（∀P∈R² ）（ d( P, A )＜δ⇒ d ( f (P), f (A) )＜ε）
　　* d ( P, A )は、2次元平面R²上での点Pと点Aとの距離を、
　　　d ( f (P), f (A) )は、R上のf (P)とf (A)との距離| f (P)−f (A)|を表す。

* 「P→Aのときf(P)が収束する」の定義では、 ０＜d( P, A )＜δ であった。
　　つまり、関数の｢極限｣では、P＝Aを除外して考えたが、
　　　　　「連続」ではP＝Aを除外しないことになる。

[文献]
小平『解析入門�U』定義6.2

(p.260);
吹田新保
『理工系の微分積分学』p.160;
杉浦『解析入門I』命題6.5-b(p.55-56);
ルディン『現代解析学』4.5(p.83):一般の距離空間上で。

※ユークリッド距離が定められたユークリッド空間R²における連続概念　
　2変数関数f (P)=f (x,y)、すなわち「『2次元平面R²の部分集合』から『実数体R』への写像」を扱う際には、
　特別な目的がない限り、
　2次元平面R²上の距離をユークリッド距離で定めて、2次元平面R²をユークリッド平面R²とし、　
　実数体Rの距離をユークリッド距離で定めて、Rを1次元ユークリッド空間Rとする設定のもとで
　考えるのが普通。　
　この設定下では、
　　　　　
　　　　d ( f (P), f (A) )=| f (P)−f (A)|=| f (x,y)−f (a,b)|　　
　だから、
　「f (P)=f (x,y)は、点A(a,b)で連続である」の定義は、具体的には
　　┌任意の（どんな）正の実数εに対して（でも）、ある正の実数δが存在して、
　　｜　　「　
　　｜　　　　　　　　ならば 　| f (x,y)−f (a,b)|＜ε」　
　　└を成り立たせる
　　（∀ε>０）（∃δ>０）（∀x,y∈R ）（⇒| f (x,y)−f (a,b)|＜ε）　
　となる。

* 小平『解析入門II』定義6.2(p.260)は、
　「f (P)=f (x,y)は、点A(a,b)で連続である」の定義を、さらに簡略化して、
　「任意の（どんな）正の実数εに対して（でも）、ある正の実数δが存在して、
　　　　『| x−a|＜δ かつ | y−b|＜δ ならば、| f(x,y)−f(a,b) |＜ε』
　　を成り立たせる」
　　（∀ε>０）（∃δ>０）（∀x,y∈R ）（（| x−a|＜δ かつ | y−b|＜δ）⇒| f (x,y)−f (a,b)|＜ε）
としている。

※2次元数ベクトル空間の上に定義されたユークリッド空間R²における連続概念　
　R²にベクトルの加法･スカラー乗法･自然な内積(標準内積)･ユークリッドノルム‖‖が定義されており、
　R²を実2次元数ベクトル空間・計量実ベクトル空間・ノルム空間として扱える場合、
　任意の実2次元数ベクトルx, y∈R²のユークリッド距離は‖x−y‖　と表せる。
　このユークリッド距離を定義したユークリッド平面R²のもとでは、　
　d( P, A )＝‖P−A‖　
　だから、
　「f (P)=f (x,y)は、点A(a,b)で連続である」の定義は、
　　「任意の（どんな）正の実数εに対して（でも）、ある正の実数δが存在して、
　　　　　『　‖P−A‖＜δ　ならば 　| f (P)−f (A)|＜ε』　　
　　　を成り立たせる」　
　　（∀ε>０）（∃δ>０）（∀P∈R² ）（‖P−A‖＜δ⇒| f (P)−f (A)|＜ε ）　
　と表せる。　　　
　ただし、上記のPは、「点P(x,y)」を表す実2次元数ベクトル(x,y)、
　　　　　上記のAは、「点A(a,b)」を表す実2次元数ベクトル(a,b)
　である。　　　　

厳密な
定義
近傍

「f (P)は点Aで連続であるcontinuous」「f (x,y)は点(a,b)で連続である」とは、
　実数f (A)の任意の（どんな）「R上のε近傍 U_ε( f (A) )」に対して（でも）、
　ある「R²上の点Aのδ近傍U_δ(A)」が存在して、
　　　　　f ( U_δ(A) ) ⊂U_ε( f (A) )　
　を満たす
ということ。
この定義を別の表現でいうと、
　任意の（どんな）正の実数εに対して（でも）、ある正の実数δが存在して、
　　　　　　　　「　f ( U_δ(A) ) ⊂U_ε( f (A) )　　」
　　　　すなわち「　(x,y)∈U_δ(A) ならば、f (x,y) ∈U_ε( f (A) )」
　を成り立たせる、
ということ。
この定義を、論理記号で表せば、
（∀U_ε( f (A) )）（∃U_δ(A)）（ f ( U_δ(A) ) ⊂U_ε( f (A)) ）　
（∀ε>０）（∃δ>０）（ f ( U_δ(A) ) ⊂U_ε( f (A) ) ）　
（∀ε>０）（∃δ>０）（∀P∈R² ）（ P∈U_δ(A) ⇒ f (P) ∈U_ε( f (A) )）　
となる。

[文献]
杉浦『解析入門I』命題6.5-c(p.55-56);

活用例

定義：右連続・左連続

不明　
cf.1変数関数についての「右連続」、１変数関数についての「左連続」　

.

→[トピック一覧：2変数関数の連続性]
→総目次

定義：2変数関数が点集合D上で連続

はじめに
読むべき
定義

「f (P)=f (x,y)は、
　　点集合D上で(二つの変数x,yについて)連続continuous」
　とは、
　f (P)=f (x,y)が点集合Dに属す各点で連続であることをいう。　　

cf.点での連続性/一様連続性

類概念：1変数関数の区間連続性/　

一般化： n変数関数/実数値関数/ベクトル値関数/距離空間上の写像/位相空間上の写像

[文献]
小平『解析入門�U』p.260;
吹田･新保『理工系の微分積分学』p.160;
杉浦『解析入門I』225.

舞台設定

厳密には、
「2変数関数が点Aで連続」の定義は、以下の手順で設定された舞台上でなされる。
Step1：平面R²を用意する。
　　　　*R²とは、実数を2個並べた組 (x,y ) をすべてあつめた集合。
　　　　　実2次元数ベクトルをすべて集めた集合でもある。
Step2：平面R²に距離dを定めて、距離空間(R²,d)を設定。
　　　　*普通は、平面R²にユークリッド距離を与えて、ユークリッド平面を考える。
Step3：平面R²上の点集合のひとつを選んで、集合Dと名づける。つまり、「D⊂R²」
　　　　*Dは、「実2次元数ベクトルの集合」とも呼べる。
Step4：平面R²上の点集合Dで定義された2変数関数 f を用意。
　　　　つまり、f : D→R　（D⊂R² ）,　z=f(P) ( z∈R, P∈D⊂R² ) ,　
　　　　　　　　z=f(x,y) ( z∈R, (x, y)∈D⊂R² )　
　　　　*fは「Dに属す各実2次元数ベクトルから実数への対応付け」だとも言える。
Step5：「平面R²上の点集合D」に属す動点を、P=(x, y)と名づける。
　　　「平面R²上の点集合D」に属す定点を、A = (a,b)と名づける。
　　　　　　　　つまり、「P, A∈D⊂R²」　
　　　　*P, Aは、「Dに属す実2次元数ベクトル」といってもよい。

厳密な
定義
ε-δ論法

「f (P)=f (x,y)は点集合D上で(二つの変数x,yについて)連続continuous」とは、
　点集合Dに属す点Aをひとつ選んで固定した上で、
　任意の正数εに対して、ある正数δをとると、
　　　「d ( P, A )＜δ　ならば、| f (P)−f (A) |＜ε」　　　…(1)
　が成り立ち、
　これが、すべての点A∈Dについてもいえるということ。
論理記号で表せば、すなわち
　( ∀ A∈D ) ( ∀ε＞0 ) ( ∃δ＞0 ) ( ∀ P∈D ) ( d ( P, A )＜δ ⇒ | f (P)−f (A) |＜ε)
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　[杉浦『解析入門I』225]
※ここで、(1)を満たすδを全てのA∈Dに対して共通に選ぶ必要はないことに注意。
　「f(P)がD上で連続」と言った場合、A∈Dの選び方で(1)を満たすδが変わってもよい。
　これに対して、
　(1)を満たすδを全てのA∈Dに対して共通に選べる、
　A∈Dの選び方によらず、εだけに対応して (1)を満たすδを一様に選べることを意味する概念は、
　一様連続性。

定義：2変数連続関数

　関数f(x,y) が定義域Dに属する全ての点で連続であるとき、
　関数f(x,y) を（2変数x,yの）連続関数と呼ぶ。

[文献]
小平『解析入門�U』p.260

定理：「2変数についての連続性」と「各変数についての連続性」との関係

f (x,y)はD上で二つの変数x,yについて連続　　　
⇒ f ( x, y ) はD上でyを固定したときxについて連続、
　　　　　　D上でxを固定したときyについて連続　　
※逆は必ずしも成り立たない。たとえば、以下の関数の(0,0)での連続性。　
　　　　　　　　　　

[文献]
小平『解析入門�U』p.260
和達『微分積分』pp.115-6;

→[トピック一覧：2変数関数の連続性]
→総目次

[space1:adwords]

定理：2変数関数の点における連続性の、点列・数列の収束への言い換え　

→ 1変数関数の連続の、数列の収束への言い換え
→ n変数関数の連続の、点列･数列の収束への言い換え
→ 距離空間のあいだの写像の連続性の、点列の収束への言い換え

要旨

２変数関数f の連続性は、収束点列の像の数列の収束に、言いかえられる。　

定理

次の命題P,Q,Rは互いに言い換え可能である。
つまり、命題P⇔命題Q⇔命題R。

命題P：
　f (P)＝f (x,y)は、点A＝(a,b)で連続　

[文献]
吹田・新保『理工系の微分積分学』p. 160.

命題Q：
　どんなR²上の点列{ P_n }={ P₁ , P₂ , P₃,…}={ (x₁ ,y₁ ) , (x₂ ,y₂ ), (x₃ ,y₃ ),…}についてであれ、　
　　その点列{ P_n }={ P₁ , P₂ , P₃,…}={ (x₁ ,y₁ ) , (x₂ ,y₂ ), (x₃ ,y₃ ),…}が点A(a,b)に収束する限り、　
　その点列の各項 P₁ , P₂ , P₃,…を２変数関数f によりR上に写した像の数列　
　　　　{ f ( P_n ) }={ f ( P₁ ), f ( P₂ ) , f ( P₃ ) ,… }={ f ( x₁ ,y₁ ) , f (x₂ ,y₂ ), f (x₃ ,y₃ ),… }
　は実数f (A)＝f (a,b)に収束する。
　つまり、
　　任意のR²上の点列{ P_n }={ P₁ , P₂ , P₃,…}={ (x₁ ,y₁ ) , (x₂ ,y₂ ), (x₃ ,y₃ ),…}について、
　　　　　　　　　　　　　　　　　P_n→A (n→∞) ならば、f (P_n)→f (A) (n→∞)　　
　論理記号で表すと、
　　　（∀{ P_n }）（（ P_n→A (n→∞) ）⇒（ f (P_n)→f (A) (n→∞)））

命題R：いかなる「実数aに収束する数列{ x₁ , x₂ , x₃ ,…}」と
　　　　　　　　「実数bに収束する数列{ y₁ , y₂ , y₃ ,…}」に対しても、
　　　　数列
　　　　　　{ f ( P_n ) }={ f ( P₁ ) , f ( P₂ ), f ( P₃ ),…}={ f ( x₁ ,y₁ ) , f (x₂ ,y₂ ), f (x₃ ,y₃ ),…}
　　　　が実数f (A)＝f (a,b)に収束する。
　　　　つまり、
　　　（∀ { x_n } { y_n } ）（（x_n→a (n→∞) かつ y_n→b (n→∞)）⇒（f (x_n ,y_n)→f (A) (n→∞)））
※なぜ？
　　関数の収束の定義と、関数の連続性の定義を見比べたうえで、
　　関数の収束と点列の収束の関連性についての定理を、関数の連続性向けに修正。　

活用例

→[トピック一覧：2変数関数の連続性]
→総目次

定理：2変数関数の和差積商の連続性

設定

この定理は、以下の手順で設定された舞台上で成立する。　
Step1：平面R²を用意する。
　　　　*R²とは、実数を2個並べた組 (x,y ) をすべてあつめた集合。
　　　　　実2次元数ベクトルをすべて集めた集合でもある。
Step2：平面R²に距離dを定めて、距離空間(R²,d)を設定。
　　　　*普通は、平面R²にユークリッド距離を与えて
　　　　　　　　　　　　　　ユークリッド平面を考える。　
Step3：平面R²上の点集合のひとつを選んで、集合Dと名づける。
　　　　つまり、「D⊂R²」　
　　　　*Dは、「実2次元数ベクトルの集合」とも呼べる。　
Step4：平面R²上の点集合Dで定義された2変数関数 f を用意。
　　　　つまり、f : D→R　（D⊂R² ）　
　　　　　　　　z=f(P) ( z∈R, P∈D⊂R² ) ,　
　　　　　　　　z=f(x,y) ( z∈R, (x, y)∈D⊂R² )　
　　　　*fは「Dに属す各実2次元数ベクトルから実数への対応付け」
　　　　　だとも言える。
Step5：「平面R²上の点集合D」に属す動点を、P=(x, y)と名づける。　
　　　「平面R²上の点集合D」に属す定点を、A = (a,b)と名づける。　
　　　　つまり、「P, A∈D⊂R²」　　
　　　　*P, Aは、「Dに属す実2次元数ベクトル」といってもよい。

[具体例] 1変数関数の和差積商の連続性
[一般化] n変数関数の和差積商の連続性/実数値関数一般の和差積商の連続性　

[文献]
小平『解析入門�U』p.261
吹田・新保『理工系の微分積分学』p. 160.

定理1

2変数関数f (P)＝f (x,y)が、点A＝(a,b)において連続であり、
かつ
2変数関数g (P)＝g (x,y)が、点A＝(a,b)において連続である
ならば、
2変数関数f ( P )±g ( P )＝f (x,y)±g (x,y)もまた、点A＝(a,b)において連続となる

定理2

2変数関数f (P)＝f (x,y)が、点A＝(a,b)において連続であるならば、
任意の定数k∈Rにたいして、 kf ( P )＝kf (x,y)もまた、点A＝(a,b)において連続となる。

定理3

2変数関数f (P)＝f (x,y)が、点A＝(a,b)において連続であり、
かつ
2変数関数g (P)＝g (x,y)が、点A＝(a,b)において連続である
ならば、
2変数関数f ( P ) g ( P )＝f (x,y) g (x,y)もまた、点A＝(a,b)において連続となる。

定理4

f (P)＝f (x,y)が、点A＝(a,b)において連続であり、
かつ
g (P)＝g (x,y)が、点A＝(a,b)において連続であり、
かつ
f(A)＝f(a,b)≠０
ならば、
2変数関数g( P )／f( P )＝g(x,y)／f(x,y)もまた、点A＝(a,b)において連続となる.

証明

関数の極限値どおしの演算についての定理より。

→[トピック一覧：2変数関数の連続性]
→総目次

[space2:7&y]

定理：合成関数compositionの連続性

要旨

二つの連続関数の合成関数は連続。

設定

この定理は、以下のように設定された舞台上で成立する。　
平面R²：実数を2個並べた組 (x,y ) をすべてあつめた集合。
　　　　※これは実2次元数ベクトルをすべて集めた集合でもある
(R²,d)　：平面R²に距離dを与えてつくった距離空間。　
　　　　　普通は、
　　　　　平面R²にユークリッド距離を与えたユークリッド平面　
　　　　　を考える。　
D ：平面R²上の点集合。つまり、D⊂R² 。
E ：平面R²上の点集合。つまり、E⊂R² 。
　　　※D,Eは、「実2次元数ベクトルの集合」とも呼べる。　
A=(a,b)：平面R²上の点集合Dに属す定点。つまり、A=(a,b)∈D⊂R²
　　　※ある特定の「Dに属す実2次元数ベクトル」といってもよい。
P=(x, y)：平面R²上の点集合Dに属す動点。つまり、P=(x, y)∈D⊂R²　

一般化：距離空間のあいだの合成写像の連続性　

[文献]
小平『解析入門�U』p.261
吹田・新保『理工系の微分積分学』p. 160.
高橋『経済学とファイナンスのための数学』p.146:ベクトル値関数のケース;

f：平面R²上の点集合Dで定義された2変数関数。　
　　　つまり、f : D→R　（D⊂R² ）　
　　　　　　　z=f(P) ( z∈R, P∈D⊂R² ) ,　z=f(x,y) ( z∈R, (x, y)∈D⊂R² )　
g：平面R²上の点集合Dで定義された2変数関数。　
　　　つまり、g : D→R　（D⊂R² ）　
　　　　　　　z=g(P) ( z∈R, P∈D⊂R² ) ,　z=g(x,y) ( z∈R, (x, y)∈D⊂R² )　
　　　※f,gは「Dに属す各実2次元数ベクトルから実数への対応付け」だとも言える。
φ：平面R²上の点集合Eで定義された2変数関数。　
　　　つまり、φ : E→R　（E⊂R² ）　
　　　　　　　z=φ(Q) ( z∈R, Q∈E⊂R² ) ,　z=φ(x,y) ( z∈R, (x, y)∈E⊂R² )　
　　　※φは「Eに属す各実2次元数ベクトルから実数への対応付け」だとも言える。

定理

2変数関数f (P)＝f (x,y)が、R²上の点集合Dで連続であり、
かつ
2変数関数g (P)＝g (x,y)が、R²上の点集合Dで連続であり、
かつ
点集合Dに属す任意の点P=(x, y)にたいして、
　　　　点( f (P), g (P) )=( f (x,y), g(x,y) )がR²上の点集合Eに属す
ならば、
合成関数φ(f (P), g(P))＝φ( f (x,y), g(x,y) )は、Dで連続。

証明

小平『解析入門II』p.261をみよ。

※

関連事項：1変数関数の合成関数の連続性、二つの1変数関数と一つの2変数関数から出来た合成関数の連続性

→[トピック一覧：2変数関数の連続性]
→総目次

[space3:vc]

2変数関数の中間値定理 intermediate value theorem

要旨

弧状連結な点集合Dで連続な2変数関数fは、f (P)≠f (Q)とすると、D上でf (P)とf (Q)の間の全ての値をとる。
→詳細

※

類例：1変数関数についての中間値定理、

2変数関数の最大値・最小値定理

要旨

有界な閉集合Dで定義された2変数連続関数はそこで最大値、最小値をとる。
→詳細

※

類例：1変数関数の最大値最小値定理、

→[トピック一覧：2変数関数の連続性]
→総目次

定義：2変数関数の一様連続性 uniformly continuous

設定

「2変数関数の一様連続性」の定義は、
　以下の手順で設定された舞台上でなされる。　
Step1：平面R²を用意する。
　　　　*R²とは、実数を2個並べた組 (x,y ) をすべてあつめた集合。
　　　　　実2次元数ベクトルをすべて集めた集合でもある。
Step2：平面R²に距離dを定めて、距離空間(R²,d)を設定。
　　　　*普通は、平面R²にユークリッド距離を与えて
　　　　　　　　　　　　　　ユークリッド平面を考える。　
Step3：平面R²上の点集合のひとつを選んで、集合Dと名づける。
　　　　つまり、「D⊂R²」　
　　　　*Dは、「実2次元数ベクトルの集合」とも呼べる。　
Step4：平面R²上の点集合Dで定義された2変数関数 f を用意。
　　　　つまり、f : D→R　（D⊂R² ）　
　　　　　　　　z=f(P) ( z∈R, P∈D⊂R² ) ,　
　　　　　　　　z=f(x,y) ( z∈R, (x, y)∈D⊂R² )　
　　　　*fは「Dに属す各実2次元数ベクトルから実数への対応付け」
　　　　　だとも言える。
Step5：「平面R²上の点集合D」に属す2点を、　
　　　　P = (x, y) , A = (a,b) と名づける。
　　　　　　　　つまり、「P, A∈D⊂R²」　　
　　　　*P, Aは、「Dに属す実2次元数ベクトル」といってもよい。

Cf.D上で連続：δが各A∈D毎にちがっていてもよい。

[文献]
小平『解析入門�U』定義6.3(p.262)
吹田・新保『理工系の微分積分学』p. 160.
杉浦『解析入門I』�W§4定義1(p. 225).;
��木『解析概論』10連続函数(p.28)
ルディン『現代解析学』
　　　4.18(p.88):距離空間一般上。

定義

「2変数関数f (P)＝f (x,y)が、点集合D上で一様連続uniformly continuousである」とは、
　任意の正数εに対して、ある正数δが存在して、
　　「d (P, A)＜δを満たす限りで任意の『Dの元』」P,Aについて、
　　　　　| f (P)−f (A) |＜ε
　　を成り立たせる
ということ。
論理記号で表せば、すなわち、
( ∀ε＞0 ) ( ∃δ＞0 ) ( ∀ A∈D ) ( ∀ P ∈D ) ( d (P, A)＜δ⇒| f (P)−f (A) |＜ε)
※δが、各A∈Dに対して一様にとれることを意味している点が、重要。

性質

・2変数関数f が点集合D上で一様連続ならば、f は点集合D上で連続。　　
・一般には、2変数関数f が点集合D上で連続だからといって、点集合D上で一様連続だとは限らない。
・点集合Dが有界な閉集合ならば、2変数関数f が点集合Dで一様連続であることと連続であることは同値
　→詳細　

否定命題

「2変数関数f (P)＝f (x,y)が、点集合D上で一様連続でない」とは、
　 ( ∃ε＞0 ) ( ∀δ＞0 ) ( ∃A∈D ) ( ∃ P ∈D ) ( d (P, A)＜δかつ| f (P)−f (A) |≧ε)
　　　　　　　　　　[杉浦『解析入門I』�W章積分§4連続関数の可積分性-定理4.1証明(4.4)(p. 226)]

※

関連事項：点での連続性、D上で連続 / 1変数関数の一様連続性　
Cf．D上で連続：δが各A∈D毎にちがっていてもよい。

→[トピック一覧：2変数関数の連続性]
→総目次

[space4:apple computer]