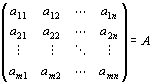証明:
行列と、数ベクトル空間から数ベクトル空間への一次写像。
[永田『理系のための線形代数の基礎』(p.26-7);斎藤『線形代数入門』2章§3(pp.44-5);
佐武『線形代数学』Ⅰ§4(pp.17-19);志賀『線形代数30講』7講(pp.42-5)10講(p.63);
ホフマン・クンツェ『線形代数学I』3.4例13(p.91);;]
(舞台設定)
K:体(例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
A:体K上の(m,n)型行列
Kn:体K上のn次元数ベクトル空間。
すなわち、Kn=K×K×…×K={ ( v1, v2, …, vn )|v1∈Kかつv2∈Kかつ…かつvn∈K }に、
ベクトルの加法とスカラー乗法を定義したもの。
ただし、Knに属すすべての n次元数ベクトルは、 n次元縦ベクトルの形式で表されているものとする。
u,v:体Kからつくった n次元縦ベクトル。
Km:体K上のm次元数ベクトル空間。
すなわち、Km=K×K×…×K={ ( v1, v2, …, vm )|v1∈Kかつv2∈Kかつ…かつvm∈K }に、
ベクトルの加法とスカラー乗法を定義したもの。
ただし、Kmに属すすべての m次元数ベクトルは、 m次元縦ベクトルの形式で表されているものとする。
(定理の確認)
「体K上のn次元数ベクトル空間」Knから
「体K上のm次元数ベクトル空間」Kmへの
任意の一次写像f:Kn→Kmにたいして、
(∀v∈Kn) ( f (v)=(Av) )
を満たす「体K上の(m,n)型行列」Aが一意的に存在する。
(
証明)
fを、任意の一次写像f:Kn→Kmとおく。
また、「体K上のn次元数ベクトル空間」Knの単位ベクトルを、e'1, e'2,…, e'nとおく。
「体K上のm次元数ベクトル空間」Kmの単位ベクトルを、e1, e2,…, emとおく。
ただし、これらのすべての単位ベクトルは、縦ベクトルとして表す。
Step1:
・写像f:Kn→Kmとしたのだから、
Knの単位ベクトルのfによる像は、すべて、Kmに属す m次元数ベクトル(ただし縦)である。
すなわち、f ( e'1 ) , f ( e'2 ) , …, f ( e'n ) ∈Km …(1-1)
・Kmに属す m次元数ベクトルは、どれでも、
Kmの単位ベクトルの一次結合として一意的に表せる。(∵)
ゆえに、(1-1)の、f ( e'1 ) , f ( e'2 ) , …, f ( e'n ) ∈Km も、すべて、
Kmの単位ベクトルの一次結合として一意的に表せる。
つまり、
f (e'1)=a11e1+a21e2+…+am1em
f (e'2)=a12e1+a22e2+…+am2em
: :
f (e'n)=a1ne1+a2ne2+…+amnem
を満たす「体K上の(m,n)型行列」
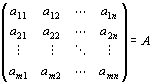
が一意的に存在する。 …(1-2)
なお、上記を、成分を表に出して書くと、
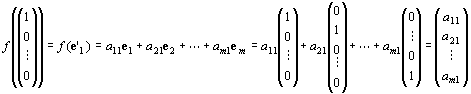
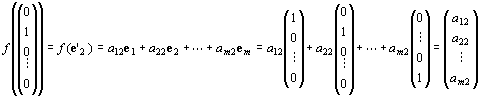
:
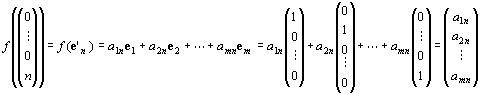
※
| f (e'1)=a11e1+a21e2+…+am1em
| f (e'2)=a12e1+a22e2+…+am2em
| : :
| f (e'n)=a1ne1+a2ne2+…+amnem
を、行列の乗法風に、
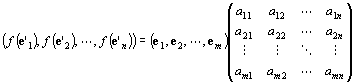
と書く、簡便法が、頻繁に用いられる。
この簡便法を用いると、上記の命題は、次のように、簡潔に表せる。
| 一次写像f:Kn→Kmにたいして、
| f (e'1, e'2, …, e'n)=(e1, e2, …, em )A
| を満たす「体K上の(m,n)型行列」Aが一意的に存在する
Step2:
Knに属す n次元数ベクトルは、どれでも、
Knの単位ベクトルの一次結合として一意的に表せる。(∵)
ゆえに、任意の n次元数ベクトルv=t(v1, v2,…, vn)∈Kn も、
Knの単位ベクトルの一次結合として一意的に
v=v1e'1+v2e'2+…+vne'n
と表せる。
Step3:
・Step2から
任意のv=t(v1, v2,…, vn)∈Kn に対して、
f (v)=f (v1e'1+v2e'2+…+vne'n)
・また、fは一次写像だから、
f (v1e'1+v2e'2+…+vne'n)=v1 f (e'1)+v2 f (e'2)+…+vn f (e'n) (∵)
・以上2点をまとめると、
任意のv=t(v1, v2,…, vn)∈Kn に対して、
f (v)=v1 f (e'1)+v2 f (e'2)+…+vn f (e'n)
Step4:
・Step3の結果に、Step1-(1-2)の結果を繰り入れると、
任意のv∈Kn に対して、
f (v)=v1 (a11e1+a21e2+…+am1em )+v2 (a12e1+a22e2+…+am2em )+…+vn (a1ne1+a2ne2+…+amnem ) (※)
を満たす「体K上の(m,n)型行列」
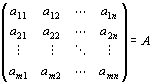
が一意的に存在する
といえる。 …(4-1)
・(※)の右辺を整理すると次のようになる。
v1 (a11e1+a21e2+…+am1em )+v2 (a12e1+a22e2+…+am2em )+…+vn (a1ne1+a2ne2+…+amnem )
= a11v1e1+a21v1e2+…+am1v1em+a12v2e1+a22v2e2+…+am2v2em+…+a1nvne1+a2nvne2+…+amnvnem
∵数ベクトル空間で定義されたスカラー乗法のベクトルに関する分配則
=(a11v1+a12v2+…+a1nvn )e1+ (a21v1+a22v2+…+a2nvn )e2+…+(am1v1+am2v2+…+amnvn )em
∵数ベクトル空間で定義されたスカラー乗法のスカラーに関する分配則
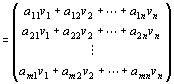 ∵単位ベクトルの定義とスカラー乗法の定義
∵単位ベクトルの定義とスカラー乗法の定義
=(Av) ∵ 行列の乗法の定義
…(4-2)
・(4-2)の結果を(4-1)に適用すると、
任意のv∈Kn に対して、
f (v)=(Av)
を満たす「体K上の(m,n)型行列」
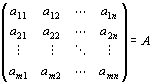
が一意的に存在する
となる。
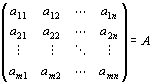
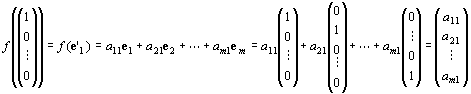
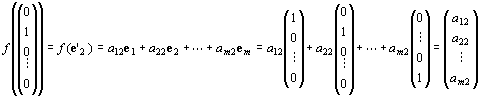
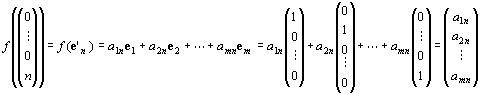
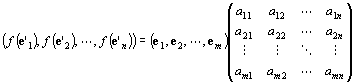
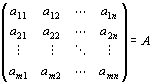
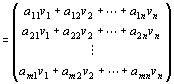 ∵単位ベクトルの定義とスカラー乗法の定義
∵単位ベクトルの定義とスカラー乗法の定義