n変数関数の極限の性質：トピック一覧　　

　　・極限値どおしの演算[極限値の和差/定数倍/積/商]　　
　　・コーシーの判定条件　　

※n変数関数の諸概念関連ページ： n変数関数の諸属性/極限/連続性/偏微分/全微分/　
※n変数関数の極限の性質の具体例：1変数関数の極限の性質/ 2変数関数の極限の性質
※n変数関数の極限の性質の一般化：ベクトル値関数の極限の性質　　
　→参考文献・総目次

定理：n変数関数の極限値どおしの演算

舞台
設定

f,g： n次元空間Rⁿの点集合D上の各点Pにたいして実数を対応づける n変数関数。　
　　　　つまり、定義域D⊂Rⁿとして、　f : D→R　, g : D→R　　
　　　　ないし、y=f (x₁,x₂,…,x_n),　y=g (x₁,x₂,…,x_n)　　
A=(x₀₁,x₀₂,…,x_0n)： n次元空間Rⁿの点集合D上の定点。
　　　　　　　　　　つまり、A=(x₀₁,x₀₂,…,x_0n)∈D⊂Rⁿ
P=(x₁,x₂,…,x_n)： n次元空間Rⁿの点集合上の動点。
　　　　　　　　　　つまり、P=(x₁,x₂,…,x_n)∈D⊂Rⁿ　

cf.
1変数関数の極限値どおしの演算
2変数関数の極限値どおしの演算
ベクトル値関数の極限値のベクトル和
ベクトル値関数の極限値のスカラー倍

[文献]
吹田新保『理工系の微分積分学』p.23;
杉浦『解析入門I』定理6.6(pp.57-63)：Rⁿ→R^mの関数一般について

定理1

→証明

[ sum-difference limit theorem ]　
f ( P )→c (P→A) かつ g ( P )→d (P→A)　ならば、{ f (P) ± g (P)}→c+d ( P→A )
つまり、P→Aとしたときに、f (P),g (P)が収束するならば、　
　 　

定理2

f ( P )→d (P→A) ならば、任意の実数cに対して、cf ( P )→cd ( P→A )
つまり、P→Aとしたときに、f(P),g(P)が収束するならば、　
　　　　　(c：定数)

定理3

[ product limit theorem ]　
f ( P )→c (P→A) かつ g ( P )→d (P→A)　ならば、{ f (P)g (P)}→cd ( P→A )
つまり、P→Aとしたときに、f(P),g(P)が収束するならば、　
　　　

定理4

[quotient limit theorem]　　
f ( P )→c (P→A) かつ g ( P )→d (P→A)かつc≠０　ならば、{g (P)/f (P)}→d/c ( P→A )
つまり、P→Aとしたときに、f(P),g(P)が収束し、
　なおかつ、このときのf(P)の極限値が０でないならば、　
　　 　

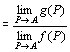
活用例

証明→定理1

P→Aとしたときにf(P)が実数値cへ収束し、かつ、 g (P)が実数値dへ収束する
　　　　つまり、f ( P )→c (P→A)かつ g ( P )→d (P→A)　
と仮定する。…(0)
[予備作業]
・関数の収束と点列･数列の収束を関係付ける定理より、
　 f ( P )→c (P→A)　
　　⇔　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n≠A) ）⇒ f (P_n)→c (n→∞)） …(1-1)
　 g ( P )→d ( P→A )　
　　⇔　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n≠A) ）⇒ g (P_n)→d (n→∞)）…(1-2)
・2変数関数h( P )=f ( P )± g ( P )　を定義する。
　関数の収束と点列･数列の収束を関係付ける定理より、
　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n≠A) ）⇒ h (P_n)→e (n→∞)） 　
　　⇔ h ( P )→e ( P→A )　
　ここで、h ( P )を、f ( P )± g ( P )に戻すと、　
　（∀{P_n}）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ {f (P_n)± g (P_n)}→e (n→∞)）
　　⇔　{f (P)± g (P)}→e ( P→A )　…(1-3)
・収束数列の演算則より、
　数列{ f (P₁), f (P₂), f (P₃),…}、{ g (P₁), g (P₂), g (P₃),…}について　
　　　f (P_n)→c (n→∞) かつ g (P_n)→d (n→∞)　　　　
　ならば、
　　f (P_n)±g (P_n)→c+d　 (n→∞)　　
　　…(1-4)
[本題]
・仮定(0)のもとで、
　　(1-1)　(1-2)　(1-4)より、
　（∀{ P_n}）（（ P_n→A (n→∞)かつ(∀n) (P_n≠A) ）⇒ f (P_n)→c (n→∞)かつ g (P_n)→d (n→∞)　
　　　　　　　　　　　　　　　　　　　　　　　　　　　⇒　f (P_n)±g (P_n)→c+d (n→∞)　　）
　　　…(1-5)　
・(1-5)は、(1-3)を用いて、{f (P)±g (P)}→c+d ( P→A )　と言い表せる。
　したがって、
　仮定(0)「 f ( P )→c (P→A) かつ g ( P )→d (P→A)」のもとで、
　{ f (P)±g (P)}→c+d ( P→A )である　。

→戻る

証明→定理2

証明→定理3

証明→定理4

→[トピック一覧：n変数関数の極限の性質]
→総目次　

定理：コーシーの判定条件　[P→ Aのとき]

舞台
設定

f： n次元空間Rⁿの点集合Dで定義された n変数関数。　
　　つまり、定義域D⊂Rⁿとして、f : D→R　　　
　　ないし、y=f (x₁,x₂,…,x_n)　　
A=(x₀₁,x₀₂,…,x_0n)： n次元空間Rⁿの点集合D上の定点。
　　　　　　　　　　つまり、P₀=(x₀₁,x₀₂,…,x_0n)∈D⊂Rⁿ
P=(x₁,x₂,…,x_n)： n次元空間Rⁿの点集合上の動点。
　　　　　　　　　　つまり、P=(x₁,x₂,…,x_n)∈D⊂Rⁿ　　

Cf.
1変数関数の場合のコーシーの判定法
2変数関数の場合のコーシーの判定法
ベクトル値関数の場合のコーシーの判定法

[文献]
小平『解析入門�U』§6.4(p.309):結論のみ。
杉浦『解析入門I』pp.61-62:証明付.
��木『解析概論』9極限(pp.22-3).

定理

次の命題S,T,Rは互いに言い換え可能である。
つまり、命題S⇔命題T⇔命題R

命題S :
　P→Aのとき、Dを定義域とする関数f (P)が収束する　
命題T :
　任意の正数εに対して、ある正数δをとると
　　任意のP,Q∈D　にたいして、　　
　　　「（０＜d(P,A)＜δかつ０＜d(Q,A)＜δ）ならば、|f (P)−f (Q)|＜ε」
　　　　　　　　　　　　　　＊　 d( P, A )は点Pと点Aとの距離を表す。
　が成り立つ。
　論理記号では、
　(∀ε>０) (∃δ>０)
　　　(∀P,Q∈D) ((０<d(P,A)<δかつ０<d(Q,A)<δ）⇒|f (P)−f (Q)|＜ε)
命題U :
　任意の正数εに対して、あるRⁿ上の点Aの除外δ近傍U*_δ(A)とると、
　　任意のP,Q∈(U*_δ(A)∩D)にたいして、|f (P)−f (Q)|＜εが成り立つ。
　論理記号では、
　(∀ε>０) (∃U*_δ(A)) (∀P,Q∈(U*_δ(A)∩D)) (|f (P)−f (Q)|＜ε)
　　　　

活用例

→[トピック一覧：n変数関数の極限の性質]
→総目次