|
| lim |
f(x) | =A 、 | lim |
g(x) | =B とすると、 |
| x→x0 | x→x0 |
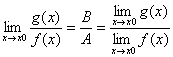 →証明
→証明
|
→戻る →[トピック一覧:1変数関数の極限の性質] →総目次 |
|
→戻る →[トピック一覧:1変数関数の極限の性質] →総目次 |
|
→戻る →[トピック一覧:1変数関数の極限の性質] →総目次 |
|
→戻る →[トピック一覧:1変数関数の極限の性質] →総目次 |
|
→戻る →[トピック一覧:1変数関数の極限の性質] →総目次 |