コーシーの判定条件 [x→x0−0のとき] の証明
以下のP,Qは同値。
P: x→x0−0のときf(x)が収束する
Q: 任意の正数εに対して、
「−δ＜x−x0＜0かつ−δ＜x'−x0＜0ならば、| f(x)−f(x') |＜ε」
つまり「 x, x'∈( x0−δ, x0 )ならば、| f(x)−f(x') |＜ε」
を成り立たせる、ある正数δが存在するということ、
すなわち、 ∀ε>0 ∃δ>0 ∀ x, x' （ x, x'∈( x0−δ, x0 )⇒| f(x)−f(x') |＜ε)
[杉浦『解析入門』pp. 61→53は、片側極限も含む一般的な議論を展開]
※広義積分の収束についてのコーシーの判定条件で使われているが、
これを明示したテキストが見当たらないので、
1.x→ x0のときの判定条件をベースに、自力でカスタマイズしつつ、
2. 杉浦『解析入門』pp.61→53の、より一般的な議論から特殊具体的を導く
ことによって、以下を作成した。よって要確認。
[P⇒Qの証明] Pが成立するという仮定の下では、いつでもQが成立することを示す。
（準備1：仮定を言い換えると…）
Pにおいて「x→x0−0のときのときf(x)が収束」とされたが、その際の収束先(左極限)をAとおく。
すなわち、
P: f(x) →A（x→x0−0）
これは、左極限の定義に従って、以下のように書き下せる。
「任意の（どんな）正の実数εに対して（でも）、
「 −δ＜x−x0＜0 ならば、 | f(x)−A|＜ε 」
つまり「 x∈( x0−δ, x0 )ならば、 f(x) ∈( A−ε,A＋ε) 」
を成り立たせる、ある正の実数δが存在する。」
すなわち、(∀ε>0)(∃δ>0) (∀ x) (0＜x−x0＜δ⇒| f(x)−A|＜ε)
ここで、εは正の実数なら任意であるから、ε/２と置いてもよい。
すると、
「任意の正の実数ε/２に対して、
「 −δ＜x−x0＜0ならば、 | f(x)−A|＜ε/２ 」
つまり「 x∈( x0−δ, x0 )ならば、f(x)∈( A−ε/２,A＋ε/２) 」
を成り立たせる、ある正の実数δが存在する。」
すなわち、(∀ε/２>0)(∃δ>0) (∀ x) (−δ＜x−x0＜0⇒| f(x)−A|＜ε/２) …(1)
となる。
(準備2)
|f(x)−f(x') |＝|f(x)−A＋A−f(x') |≦|f(x)−A|＋|A−f(x') | ∵絶対値の性質
…(2)
Pが成立するという仮定のもとでは、(1)より、
「任意の正の実数ε/２に対して、
−δ＜ x'−x0 ＜0 ならば、 | f(x')−A|＜ε/２
つまり x'∈( x0−δ, x0 )ならば、f(x') ∈( A−ε/２,A＋ε/２)
を成り立たせる、ある正の実数δが存在する」
すなわち、(∀ε/２>0)(∃δ>0) (∀ x') (−δ＜ x'−x0 ＜0 ⇒| f(x)−A|＜ε/２)
も成り立つ。
すると、これと、もとの(1)をあわせて、Pが成立するという仮定のもとでは、以下が成立する。
「任意の正の実数ε/２に対して、
(−δ＜x−x0＜0かつδ＜ x'−x0 ＜0)ならば、(| f(x)−A|, ＜ε/２かつ| f(x')−A|＜ε/２) …※
を成り立たせる、ある正の実数δが存在する」
ここで、この※の部分を以下のように、言い換えられる。
「任意の正の実数ε/２に対して、
−δ＜x−x0＜0かつ−δ＜ x'−x0 ＜0ならば、
| f(x)−A|+ | f(x')−A|=| f(x)−A|+ | A− f (x') |＜ε …※
を成り立たせる、ある正の実数δが存在する」
すなわち、
(∀ε/２>0)(∃δ>0) (∀ x, x') (−δ＜x−x0＜0かつ−δ＜ x'−x0 ＜0⇒| f(x)−A|+ | f(x')−A|＜ε)
さらに、この※の部分を(2)に接続すると、以下のようになる。
「任意の正の実数ε/２に対して、
−δ＜x−x0＜0かつ−δ＜ x'−x0 ＜0ならば、
|f(x)−f(x') |≦| f(x)−A|+ | A− f (x') |＜ε …※
を成り立たせる、ある正の実数δが存在する」
これを簡潔にいうと、
「任意の正の実数ε(ε/２が任意なのだから、εも任意)に対して、
−δ＜x−x0＜0かつ−δ＜ x'−x0 ＜0ならば、|f(x)−f(x') |＜ε
を成り立たせる、ある正の実数δが存在する」
すなわち、
(∀ε>0)(∃δ>0) (∀ x, x') ((−δ＜x−x0＜0かつ−δ＜ x'−x0 ＜0)⇒|f(x)−f(x') |＜ε)
よって、P: f(x) →A（x→x0−0）が成立するという仮定の下ではいつでも、結論Qが成立することが示された。
[Q ⇒ Pの証明]
Q「(∀ε>0)(∃δ>0)(x, x'∈( x0−δ, x0 )⇒|f(x)−f(x') |＜ε)」が成立するという仮定の下では、
いつでもP「x→x0−0のときf(x)が収束」が成立することを示す。
（方針）
「f(x) →A（x→x0−0）」と「1.全ての項がx0より小、かつ、2.x0 に収束するの2点を満たす限りで任意の数列 { xn }をとると、そのfによる像の数列{ f ( xn ) }→A(n→∞)」が同値であるとの定理より、
P「f(x) →A（x→x0−0）」は、
P'「1.全ての自然数n≧1についてxn＜x0かつ、2.x0 に収束するの2点を満たす限りで任意の数列 { xn }に対して、{ f ( xn ) }→A(n→∞)」と言い換え可能。
したがって、Qが成立するという仮定のもとで、いつでもP'が成立することを示せば、
Qが成立するという仮定のもとで、いつでもPが成立することを示したことになる。
(仮定の確認)
Qが成立するという仮定のもとでは、
任意の（どんな）正の実数εに対して（でも）、
「 −δ＜x−x0＜0かつ−δ＜x'−x0＜0ならば、|f(x)−f(x') |＜ε 」
つまり「 x, x'∈( x0−δ, x0 )ならば、|f(x)−f(x') |＜ε 」…※
を成り立たせる、ある正数δが存在する
すなわち、(∀ε>0)(∃δ>0)(x, x'∈( x0−δ, x0 )⇒|f(x)−f(x') |＜ε) …(1)
（準備）
{ xn }を、
「全ての自然数n≧1についてxn＜x0」かつ「x0 に収束する」の2点を満たす限りで任意の数列とする。…(2)
数列の収束の厳密な定義にしたがって、(2)を書き下すと、
任意の（どんな小さな）正の実数ε’に対して（でも）、
「n≧Nならば、 0＜| xn −x0|= x0−xn＜ε’」(∵0＜| xn −x0|= x0−xnは(2)のxn＜x0から)
簡単にして「n≧Nならば、 −ε'＜xn− x0＜0」
つまり「n≧Nならば、xn∈( x0−ε' , x0) 」
を満たす、ある（十分大きな）自然数Nが存在する。」
すなわち(∀ε’>0)(∃N∈N)(∀n∈N)( n≧N⇒ ( x0−ε' , x0)) …(3)
となる。
＊ ＊ ＊
(3)は、「ε'は任意の正の実数に対しても…を満たすNが存在する」というのだから、
ε'を「Qが成立するという仮定のもとで(1)によって存在が保証された、※を成立させるδ」に代えても、「…を満たすNが存在する」ことにかわりない。
よって、
「全ての自然数n≧1についてx0＜xn」かつ「x0 に収束する」の2点を満たす限りで任意の数列{ xn }について、
「n≧Nならば、 −δ＜xn− x0＜0つまりxn∈( x0−δ, x0) 」
を満たす、ある（十分大きな）自然数Nが存在する
すなわち (∃N∈N)(∀n∈N)( n≧N⇒ xn∈( x0−δ, x0) ) …(4)
が成立する。
＊ ＊ ＊
ゆえに、数列 { xn }では、(4)で決まったN番目以上の任意の2項xl ,xm( l,m≧N)に対して、
−δ＜xl− x0＜0 かつ −δ＜xm− x0＜0 つまり、xl ,xm∈( x0−δ, x0)
すなわち (∃N∈N) (∀l,m ∈N)( l,m≧N⇒ xl ,xm∈( x0−δ, x0) ) …(5)
が成立する。
ただし、ここでのδは「Qが成立するという仮定のもとで(1)によって存在が保証された、※を成立させるδ」であることに注意。
(本題)
「全ての自然数n≧1についてxn＜x0」かつ「x0 に収束する」の2点を満たす限りで任意の数列{ xn }の、
(4)で決まったN番目以上の任意の2項xl ,xmは、(5)より、
(1)における「−δ＜x−x0＜0かつ−δ＜x'−x0＜0ならば」つまり「x, x'∈( x0−δ, x0) ならば」を満たすx, x'である。
ゆえに、Qが成立するという仮定のもとでは、(1)より、
|f( xl )−f( xm ) |＜ε ( l,m≧N )
がいつでも成り立つことになる。
これは、コーシー列の定義に他ならない。数列{ f(xn ) }はコーシー列である。
つまり、
Qが成立するという仮定のもとでは、つねに、
「全ての自然数n≧1についてxn＜x0」かつ「x0 に収束する」の2点を満たす限りで任意の数列{ xn }
にたいして、そのfによる像の数列{ f(xn ) }はコーシー列となる …(6)
のだ。
＊ ＊ ＊
(6)は定理「数列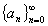
が収束するための必要十分条件は、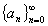がコーシー列であること。」により、
Qが成立するという仮定のもとでは、つねに、
「全ての自然数n≧1についてxn＜x0」かつ「x0 に収束する」の2点を満たす限りで任意の数列{ xn }
にたいして、そのfによる像の数列{ f(xn ) }は収束する。…(7)
と言いかえられる。
＊ ＊ ＊
さらに、
(7)は
「f(x) →A（x→x0−0）」と
「1.全ての項がx0より小、かつ、2.x0 に収束するの2点を満たす限りで任意の数列 { xn }をとると、
そのfによる像の数列{ f ( xn ) }→A(n→∞)」
が同値である
との定理により、
Qが成立するという仮定のもとでは、つねに、x→x0−0のときf(x)が収束する
と言いかえられる。
以上、
Q:「任意の正数εに対して
−δ＜x−x0＜0かつ−δ＜x'−x0＜0ならば、 |f(x)−f(x') |＜ε
を成立させる、正数δが存在する。」
が成り立つという仮定のもとでは、
つねに、
「全ての自然数n≧1についてxn＜x0」かつ「x0 に収束する」の2点を満たす限りで任意の数列{ xn }にたいして、数列{ f(xn ) }は収束する
すなわち、x→x0−0のときf(x)が収束することを示した。
（reference）
『岩波数学辞典（第三版）』.項目166(pp436).
吉田耕作・栗田稔・戸田宏『平成元年3/31文部省検定済高等学校数学科用 高等学校 微分・積分 新訂版』啓林館、pp.28-33.
小平邦彦『解析入門I (軽装版) 』岩波書店、2003年、pp.78-9。
吹田・新保『理工系の微分積分学』学術図書出版社、1987年、pp.20-23.
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、p.95.
和達三樹『理工系の数学入門コース1・微分積分』岩波書店、1988年、pp.27-28.
杉浦光夫『解析入門』東京大学出版会、1980年、pp.57-63.
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.32-36;42-44.
住友洸『大学一年生の微積分学』現代数学社、1987年、p.124。
Chiang, Fundamental Methods of Mathematical Economics: Third Edition, McGraw Hill,1984. pp.145-147.
Fischer,Emanuel.Intermediate Real Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Heidelberg Berlin,1983,pp. 228-231; 238-239.
Lang,Serge.Undergraduate Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1983,pp.135-143.