→戻る　

定理：コーシーの平均値定理　　
　[吹田新保『理工系の…』p.51;和達『微分積分』p.62;小平『解析入門I』p.123;高木『解析概論』p. 48;]
　　関数f(x), g(x)は閉区間[a,b]で連続、開区間(a,b)で微分可能、(a,b)で常に g' (x) ≠0ならば、
　　　　
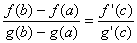
　　　を満たすcが(a,b)に存在する。　
※活用例：テイラーの定理の導出　

(コーシーの平均値定理の証明)

[高木『解析概論』p. 48. 小平『解析入門I』p.123. 吹田・新保『理工系の…』p.51. ]　

　　　　仮定：f(x), g(x)は閉区間[a,b]で連続、開区間(a,b)で微分可能　…(1)　
　　　　　　　(a,b)で常にg' (x) ≠０　　　　　　　　　　　　　　　…(2)　　
　　　　(2)より、g(a)≠g(b)　　…(3)　
　　　　なぜなら、
　　　　　　平均値定理から、g(b)−g(a)=g' (ζ)　をみたすζが(a,b)内に少なくとも一つ存在する。
　　　　　　(2)より、(a,b)内の全てのxに対しg' (x) ≠０なのだから、当然、g' (ζ) ≠０　
　　　　　　よって、g(b)−g(a)= g' (ζ) ≠０　　　
　　[関数φ(x)の設定]　　　　　
　　　　以下のように、関数φ(x)を、ロールの定理が適用可能となるように、
　　　　　　　　すなわち、閉区間[a,b]で連続、開区間(a,b)で微分可能、φ(a)=φ(b)となるように、
　　　　つくる。　　　　　
　　　　φ(x)＝{ g(b)−g(a)}{ f(x)−f(a)}−{ f(b)−f(a)}{g (x)−g(a)}
　　[ロールの定理の適用]
　　　　φ(a)＝{ g(b)−g(a)}・０−{ f(b)−f(a)}・０=０　
　　　　φ(b)＝{ g(b)−g(a)}{ f(b)−f(a)}−{ f(b)−f(a)}{g (b)−g(a)}=０　
　　　　より、確かに、φ(a)=φ(b)となる。
　　　　ロールの定理より、φ' (c)＝０　を満たすcが(a,b)内に少なくとも一つ存在する。　…(4)　
　　[φ(x)の導関数]　
　　　　ところで、
　　　　　φ(x)＝{ g(b)−g(a)}{ f(x)−f(a)}−{ f(b)−f(a)}{g (x)−g(a)}
　　　　　　　　＝{ g(b)−g(a)} f(x)−{ g(b)−g(a)}f(a)−{ f(b)−f(a)} g (x)＋g(a) { f(b)−f(a)}　　
　　　　の導関数は、　　　
　　　　　φ'(x)＝[{ g(b)−g(a)} f(x)]’−[{ g(b)−g(a)}f(a) ]’−[{ f(b)−f(a)} g (x)]’＋[g(a) { f(b)−f(a)}]’　
　　　　　　　　　　　　　　　　　　　　∵和の微分　　　　　　
　　　　　　　＝[{ g(b)−g(a)} f(x)]’−０−[{ f(b)−f(a)} g (x)]’＋0　∵定数の微分　　
　　　　　　　＝{ g(b)−g(a)} f ' (x)−{ f(b)−f(a)} g' (x)　　　　　∵関数の定数倍の微分　
　　　　(4)より、　　　
　　　　　　　φ'(c)＝{ g(b)−g(a)}f ' (c)−{ f(b)−f(a)}g' (c)=0　　　(※)
　　　　を満たすcが(a,b)内に少なくとも一つ存在する。
　　　　(※)はすなわち、　
　　　　　　　{ g(b)−g(a)}f ' (c)={ f(b)−f(a)}g'(c)　
　　　　　　　{ g(b)−g(a)}f ' (c)／g' (c)={ f(b)−f(a)}　∵(2)よりg' (c) ≠0なので両辺をg' (c)で割る。　　
　　　　　　　f ' (c)／g' (c)={ f(b)−f(a)}／{ g(b)−g(a)}　∵(3)よりg(b)−g(a)≠0なので両辺をこれで割る。