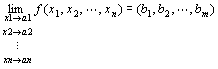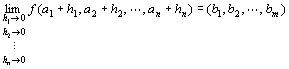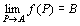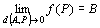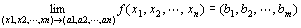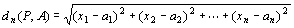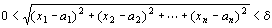|
|
|
|
定義:ベクトル値関数の収束 convergence・極限値limit |
|
→ はじめに読むべき定義/ε-δ論法による定義/近傍概念による定義
cf.1変数関数の収束・極限値/2変数関数の収束・極限値/ n変数関数の収束・極限値/距離空間上の関数の収束・極限値 |
|
はじめに
読むべき
定義 |
「 点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
ベクトル値関数 (y1 , y2 , … , ym )=f ( x1 ,x2 , … , xn ) が、点B(b1,b2,…,bm)に収束する」
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたときの、
ベクトル値関数 (y1,y2,…,ym)= f (x1,x2,…,xn)の極限は、点B(b1,b2,…,bm)である」
f ( x1 , x2 ,…, xn )→(b1,b2,…,bm) ( x1→a1 , x2→a2 ,… ,xn→an )
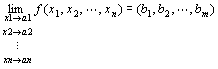 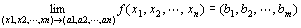
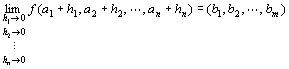 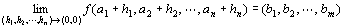
「 n次元空間Rn上の点Pを点Aに近づけたとき、
ベクトル値関数 f ( P ) が、 m次元空間Rm上の点Bに収束する」
「 n次元空間Rn上の点Pを点Aに近づけたときの、
ベクトル値関数 f ( P ) の極限は、 m次元空間Rm上の点Bである」
f ( P )→B ( P → A )
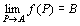 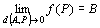
とは、
点P(x1,x2,…,xn)を、点A(a1,a2,…,an)と一致させることなく点A(a1,a2,…,an)に近づけたとき、
点P(x1,x2,…,xn)の点A(a1,a2,…,an)への接近経路にかかわらず、
ベクトル値関数 (y1 ,y2 , …, ym )= f ( x1 , x2 ,…,xn )の値(y1 ,y2 , …, ym )が
同じ1つの点B(b1,b2,…,bm)に近づくことをいう。 |
|
※ 留意点
(1)極限の定義において、点Pと点Aが一致することは除外している。
点Aがベクトル値関数f (P) = f (x1,x2,…,xn)の定義域に含まれているとは限らない。
(2) 点Pの点Aへの接近経路によって、
ベクトル値関数f (P) = f (x1,x2,…,xn)が近づく値が異なるときには、
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
ベクトル値関数f (P) = f (x1,x2,…,xn)が点B(b1,b2,…,bm)に収束しない」
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
ベクトル値関数f (P) = f (x1,x2,…,xn)に極限値は存在しない」という。
※この定義は一見わかりやすい。
ところが、「近づく」とはいかなる事態を指すのか、という点が、
明らかにされておらず、
この「収束」「極限」定義は、実のところは不正確で、
証明での使用に耐えられない。
そこで、
「近づく」の意味を明確化するために、
「収束」「極限」概念は、次のように厳密に定義される。 |
|
|
|
→ 「ベクトル値関数の収束・極限の定義」先頭 |
|
|
厳密な
定義:
ε -δ
論法 |
「 n次元空間Rn上の点Pを点Aに近づけたとき、
ベクトル値関数f (P)が m次元空間Rm上の点Bに収束する」
「 n次元空間Rn上の点Pを点Aに近づけたときの、
ベクトル値関数f (P)の極限は m次元空間Rm上の点Bである」
f ( P )→B ( P → A )
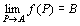 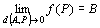
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
ベクトル値関数 f (x1,x2,…,xn)が点B(b1,b2,…,bm)に収束する」
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたときの
ベクトル値関数 f (x1,x2,…,xn)の極限は点B(b1,b2,…,bm)である」
f ( x1 , x2 ,…, xn )→(b1,b2,…,bm) ( x1→a1 , x2→a2 ,… ,xn→an )
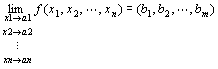 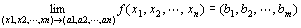
とは、
任意の(どんな)正の実数εに対して(でも)、ある正の実数δをとると、
0<dn( P, A )<δ ⇒ dm ( f (P), B )<ε
が成り立つ
ということ。
この定義を、論理記号で表せば、
(∀ε>0)(∃δ>0)(∀P∈Rn )(0<dn ( P, A )<δ⇒dm ( f (P), B )<ε )
となる。
*dn ( P, A )は、 n次元空間Rn上での点P(x1,x2,…,xn)と点A(a1,a2,…,an)との距離を、
dm ( f (P), B )は、 m次元空間Rm上のf (P)と点B(b1,b2,…,bm)との距離を表す。 |
[ 文献]
杉浦
『解析入門I』
I§6定義2-3(pp.51-2);
黒田
『微分積分学』
定義8.6(p.277); |
|
※ユークリッド距離が定められたユークリッド空間 Rn, Rmにおける極限概念
ベクトル値関数(f1 (x1,x2,…,xn),f2 (x1,x2,…,xn),…,fm (x1,x2,…,xn)) =f (P) = f (x1,x2,…,xn)について、
収束・極限を扱う際には、
特別な目的がない限り、
n次元空間Rn上の距離をユークリッド距離で定めて、 n次元空間Rnをユークリッド空間Rnとし、
m次元空間Rmの上の距離をユークリッド距離で定めて、 m次元空間Rmををユークリッド空間Rmとする、
設定のもとで考えるのが普通。
この設定下では、
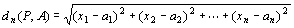
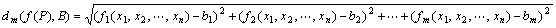
だから、
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
ベクトル値関数( f1 (x1,x2,…,xn), f2 (x1,x2,…,xn) , … , fm (x1,x2,…,xn) ) = f (x1,x2,…,xn)が点B(b1,b2,…,bm)に収束する」
「点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたときの、
ベクトル値関数( f1 (x1,x2,…,xn), f2 (x1,x2,…,xn) , … , fm (x1,x2,…,xn) ) = f (x1,x2,…,xn)の極限は点B(b1,b2,…,bm)である」
「f ( x1 , x2 ,…, xn )→(b1,b2,…,bm) ( x1→a1 , x2→a2 ,… ,xn→an )」
の定義は、具体的には
┌任意の(どんな)正の実数εに対して(でも)、
|ある正の実数δが存在して、
| 「 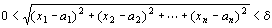
| ならば
| 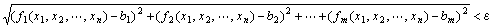 」 」
└を成り立たせる
(∀ε>0) (∃δ>0) (∀x1,x2,…,xn∈R)
(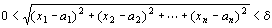
⇒
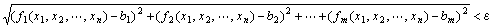 ) )
となる。 |
|
※ n次元数ベクトル空間の上に定義されたユークリッド空間R2における極限概念
・ n次元空間Rnに
ベクトルの加法・スカラー乗法・自然な内積(標準内積)・ユークリッドノルム‖‖nが定義されており、
n次元空間Rnを実n次元数ベクトル空間・計量実ベクトル空間・ノルム空間として扱える場合、
任意の実n次元数ベクトルx, y∈Rnのユークリッド距離は‖x−y‖n と表せる。
このユークリッド距離を定義したユークリッド空間Rnのもとでは、
dn( P, A )=‖P−A‖n
・ m次元空間Rmに
ベクトルの加法・スカラー乗法・自然な内積(標準内積)・ユークリッドノルム‖‖mが定義されており、
m次元空間Rmを実n次元数ベクトル空間・計量実ベクトル空間・ノルム空間として扱える場合、
任意の実m次元数ベクトルx', y'∈Rmのユークリッド距離は‖x−y‖m と表せる。
このユークリッド距離を定義したユークリッド空間Rmのもとでは、
dm( f (P), B )=‖f (P)−B‖m
・したがって、
「 n次元空間Rn上の点Pを点Aに近づけたとき、ベクトル値関数f (P) が、 m次元空間Rm上の点Bに収束する」
「 n次元空間Rn上の点Pを点Aに近づけたときの、ベクトル値関数f (P) の極限は m次元空間Rm上の点Bである」
「 f ( P )→B ( P → A ) 」
の定義は、具体的には
┌任意の(どんな)正の実数εに対して(でも)、
|ある正の実数δが存在して、
| 「 0<‖P−A‖n<δ ならば ‖f (P)−B‖m<ε 」
|
└を成り立たせる
(∀ε>0)(∃δ>0)(∀P∈Rn )(0<‖P−A‖n<δ⇒‖ f (P)−B‖m<ε )
と表せる。
ただし、上記のPは、「点P(x1,x2,…,xn)」を表す実n次元数ベクトル(x1,x2,…,xn)、
上記のAは、「点A(a1,a2,…,an)」を表す実n次元数ベクトル(a1,a2,…,an)、
上記のBは、「点B(b1,b2,…,bn)」を表す実m次元数ベクトル(b1,b2,…,bn)
である。 |
|
|
→ 「ベクトル値関数の収束・極限の定義」先頭 |
|
|
近傍を
用いた
定義 |
「 n次元空間Rn上の点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
ベクトル値関数f (P) = f (x1,x2,…,xn)が、
m次元空間Rm上の点B(b1,b2,…,bm)に収束する」
「 n次元空間Rn上の点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたときの、
ベクトル値関数f (P) = f (x1,x2,…,xn)の極限は
m次元空間Rm上の点B(b1,b2,…,bm)である」
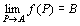 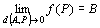
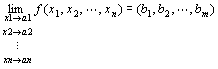
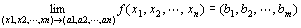
とは、
点Bの任意の「Rm上のε近傍 Uε(B)」に対して(でも)、
ある「Rn上の点Aの除外δ近傍U*δ(A)」が存在して、
f ( U*δ(A) ) ⊂ Uε(B)
を満たす
ということ。
この定義を別の表現でいうと、
任意の(どんな)正の実数εに対して(でも)、ある正の実数δが存在して、
「 f ( U*δ(A) ) ⊂ Uε(B) 」
すなわち「 P∈ U*δ(A) ならば、 f (P) ∈Uε(B) 」
を成り立たせる、
ということ。
この定義を、論理記号で表せば、
(∀Uε(B))(∃ U*δ(A) )( f ( U*δ(A) ) ⊂ Uε(B) )
(∀ε>0)(∃δ>0)( f ( U*δ(A) ) ⊂ Uε(B) )
(∀ε>0)(∃δ>0)(∀P∈Rn )( P∈ U*δ(A) ⇒ f (P) ∈Uε(B))
となる。 |
[ 文献]
|
|
※ユークリッド距離が定められたユークリッド空間 Rnにおける極限概念
ベクトル値関数f (P) について、
収束・極限を扱う際には、
特別な目的がない限り、
n次元空間Rn上の距離をユークリッド距離で定めて、 n次元空間Rnをユークリッド空間Rnとし、
実数体Rの距離をユークリッド距離で定めて、Rを1次元ユークリッド空間Rとする、
設定のもとで考えるのが普通。
この設定のもとでは、
点A(a1,a2,…,an)の「Rn上の点Aの除外δ近傍U*δ(A)」は、
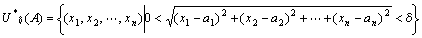
点B(b1,b2,…,bn)の「Rm上のε近傍 Uε(B)」は、
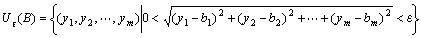
だから、
「 n次元空間Rn上の点Pを点Aに近づけたとき、ベクトル値関数f (P) が、 m次元空間Rm上の点Bに収束する」
「 n次元空間Rn上の点Pを点Aに近づけたときの、ベクトル値関数f (P) の極限は m次元空間Rm上の点Bである」
「 f ( P )→B ( P → A ) 」
の定義は、具体的には
┌任意の(どんな)正の実数εに対して(でも)、
|ある正の実数δが存在して、
| 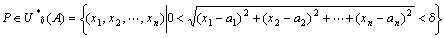
| ならば
| 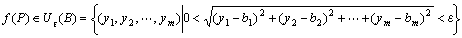
└を成り立たせる
となる。 |
|
※ n次元数ベクトル空間の上に定義されたユークリッド空間Rnにおける極限概念
・ n次元空間Rnに
ベクトルの加法・スカラー乗法・自然な内積(標準内積)・ユークリッドノルム‖‖nが定義されており、
n次元空間Rnを実n次元数ベクトル空間・計量実ベクトル空間・ノルム空間として扱える場合、
任意の実n次元数ベクトルx, y∈Rnのユークリッド距離は‖x−y‖n と表せる。
このユークリッド距離を定義したユークリッド空間Rnのもとでは、
点A(a1,a2,…,an)の「Rn上の点Aの除外δ近傍U*δ(A)」は、U*δ(A)={ Q∈Rn | 0<‖Q−A‖<ε }
・ m次元空間Rmに
ベクトルの加法・スカラー乗法・自然な内積(標準内積)・ユークリッドノルム‖‖mが定義されており、
m次元空間Rmを実n次元数ベクトル空間・計量実ベクトル空間・ノルム空間として扱える場合、
任意の実m次元数ベクトルx', y'∈Rmのユークリッド距離は‖x−y‖m と表せる。
このユークリッド距離を定義したユークリッド空間Rmのもとでは、
点B(b1,b2,…,bn)の「Rm上のε近傍 Uε(B)」は、Uε(B)={ Q∈Rm | ‖Q−B‖<ε }
・だから、
「 n次元空間Rn上の点Pを点Aに近づけたとき、ベクトル値関数f (P) が、 m次元空間Rm上の点Bに収束する」
「 n次元空間Rn上の点Pを点Aに近づけたときの、ベクトル値関数f (P) の極限は m次元空間Rm上の点Bである」
「 f ( P )→B ( P → A ) 」
の定義は、
┌任意の(どんな)正の実数εに対して(でも)、
|ある正の実数δが存在して、
| P∈U*δ(A)={ Q∈Rn | 0<‖Q−A‖<δ }
| ならば
| f (P) ∈Uε(B)={ Q∈Rm | ‖Q−B‖<ε }
└を成り立たせる
と表せる。
ただし、上記のPは、「点P(x1,x2,…,xn)」を表す実n次元数ベクトル(x1,x2,…,xn)、
上記のAは、「点A(a1,a2,…,an)」を表す実n次元数ベクトル(a1,a2,…,an)、
上記のBは、「点B(b1,b2,…,bn)」を表す実m次元数ベクトル(b1,b2,…,bn)
である。 |
|
|
→[
|
定理:「ベクトル値関数の極限」の「 n変数関数の極限」への言い換え |
|
定理 |
次の命題 Pと命題Qは互いに言い換え可能である。
つまり、命題P⇔命題Q。
命題 P:
点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
ベクトル値関数 ( y1 ,y2 , …, ym )=f ( x1 , x2 , … , xn )が、
点B(b1,b2,…,bm)に収束する。
すなわち、f (x1,x2,…,xn)→(b1,b2,…,bm) ( x1→a1 , x2→a2 ,…,xn→an )
命題 Q:ベクトル値関数 ( y1 ,y2 , …, ym )=f ( x1 , x2 , … , xn )を、
m個の n変数関数の組
y1 = f1 ( x1 , x2 , … , xn )
y2 = f2 ( x1 , x2 , … , xn )
:
ym =fm ( x1 , x2 , … , xn )
として表したときに、
f1 (x1,x2,…,xn)→b1 ( x1→a1 , x2→a2 ,…,xn→an )
かつ
f2 (x1,x2,…,xn)→b2 ( x1→a1 , x2→a2 ,…,xn→an )
かつ
:
かつ
fm (x1,x2,…,xn)→bm ( x1→a1 , x2→a2 ,…,xn→an )
が満たされる。 |
[文献]
杉浦『解析入門I』I章§6定理6.8-1(p.59);
杉浦『解析演習』I章§2要綱2.16(p.11);
[活用例]
ベクトル値関数の連続性の
多変数関数の連続性への言い換え
|
|
証明 |
証明は、杉浦『 解析入門I』I章§6定理6.8-1(p.59)参照。 |
|
| |
|
|
→[
|
定理:ベクトル値関数の収束の、点列の収束への言い換え |
| |
具体例: 1変数関数の収束の、数列の収束への言い換え/ 2変数関数の収束の、点列・数列の収束への言い換え
n変数関数の収束の、点列・数列の収束への言い換え
一般化:距離空間の間の写像の収束の、点列の収束への言い換え |
|
定理 1 |
次の命題 P,Q,Rは互いに言い換え可能である。
つまり、命題P⇔命題Q⇔命題R。
命題P:
点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
ベクトル値関数 f (P) = f (x1,x2,…,xn)が、
m次元空間Rm上の点B(b1,b2,…,bm)に収束する」
これを記号で表すと、
・f ( P )→B ( P → A )
・f (x1,x2,…,xn)→(b1,b2,…,bm) ( x1→a1 , x2→a2 ,…,xn→an )
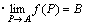
など。 |
[ 文献]
杉浦『解析入門I』定理6.2(p.53):証明付;
|
|
命題 Q:
どんなRn上の点列{ Pi }={ P1 , P2 , P3,…}={ (x11,x12,…,x1n) , (x21,x22,…,x2n) , (x31,x32,…,x3n) ,…}についてであれ、
1. その点列{ Pi }={ P1 , P2 , P3,…}={ (x11,x12,…,x1n) , (x21,x22,…,x2n) , (x31,x32,…,x3n) ,…}が点A(a1,a2,…,an)に収束し、
かつ
2. その点列の各項 P1 , P2 , P3 , … がどれも点Aと一致しない
限り、
その点列の各項 P1 , P2 , P3 , …をベクトル値関数f によりRm上に写した像の点列
{ f ( Pi ) }={ f ( P1 ), f ( P2 ) , f ( P3 ) ,… }={ f ( x11,x12,…,x1n ) , f (x21,x22,…,x2n ), f (x31,x32,…,x3n ),… }
は点B(b1,b2,…,bm)に収束する。
つまり、
任意のRn上の点列{ PI }={ P1 , P2 , P3,…}={ (x11,x12,…,x1n) , (x21,x22,…,x2n) , (x31,x32,…,x3n) ,…}について、
Pi→A (i→∞) かつ P1≠A , P2≠A , P3≠A ,…ならば、f ( Pi )→B (i→∞)
論理記号で表すと、
(∀{ Pi })(( Pi→A (i→∞)かつ(∀i) ( Pi ≠A) )⇒ f ( Pi )→B (i→∞) )
命題 R:
いかなる
「実数a1に収束する数列{ x11 , x21 , x31 ,…}」(ただし、x11≠a1 , x21≠a1 , x31≠a1 ,… )
「実数a2に収束する数列{ x12 , x22 , x32 ,…}」(ただし、x12≠a2 , x22≠a2 , x32≠a2 ,… )
:
「実数anに収束する数列{ x1n , x2n , x3n ,…}」(ただし、x1n ≠an , x2n ≠an , x3n ≠an ,… )
に対しても、
点列 { f ( Pi ) }={ f ( P1 ), f ( P2 ) , f ( P3 ) ,… }={ f ( x11,x12,…,x1n ) , f (x21,x22,…,x2n ), f (x31,x32,…,x3n ),… }
が点B(b1,b2,…,bm)に収束する。
つまり、
(∀ { xi1 } ,{ xi2 }, …, { xin } )
(((∀i) (xi1≠a1かつxi2≠a2かつ…かつxin≠an)かつxi1→a1 (i→∞)かつxi2→a2 (i→∞)かつ…かつxin→an (i→∞))
⇒ f ( xi1,xi2,…,xin ) →B (i→∞))
※なぜ?
・「命題P⇒命題Q」となるわけ→[杉浦『解析入門I』定理6.2(p.53)]
・「命題Q⇒命題P」となるわけ→[杉浦『解析入門I』定理6.2(p.53)]
・「命題Q⇔命題R」となるのは、点列の収束と数列の収束の関係による。 |
|
定理 2 |
次の命題 P,Q,Rは互いに言い換え可能である。
つまり、命題P⇔命題Q⇔命題R。
命題P:
点P(x1,x2,…,xn)を点A(a1,a2,…,an)に近づけたとき、
ベクトル値関数 f (P) = f (x1,x2,…,xn)が収束する」
すなわち、
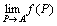
が存在する
※極限値の値をだしていないことに注意。 |
[ 文献]
杉浦『解析入門I』定理6.2系(p.54):証明付 |
|
命題 Q:
どんなRn上の点列{ Pi }={ P1 , P2 , P3,…}={ (x11,x12,…,x1n) , (x21,x22,…,x2n) , (x31,x32,…,x3n) ,…}についてであれ、
1. その点列{ Pi }={ P1 , P2 , P3,…}={ (x11,x12,…,x1n) , (x21,x22,…,x2n) , (x31,x32,…,x3n) ,…}が点A(a1,a2,…,an)に収束し、
かつ
2. その点列の各項 P1 , P2 , P3 , … がどれも点Aと一致しない
限り、
その点列の各項 P1 , P2 , P3 , …をベクトル値関数f によりRm上に写した像の点列
{ f ( Pi ) }={ f ( P1 ), f ( P2 ) , f ( P3 ) ,… }={ f ( x11,x12,…,x1n ) , f (x21,x22,…,x2n ), f (x31,x32,…,x3n ),… }
が収束する。
論理記号で表すと、
(∀{ Pi })(( Pi→A (i→∞)かつ(∀i) ( Pi ≠A) )⇒ 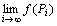 が存在する) が存在する)
※極限値の値をだしていないことに注意。
命題 R:
いかなる
「収束数列{ x11 , x21 , x31 ,…}」(ただし、x11≠a1 , x21≠a1 , x31≠a1 ,… )
「収束数列{ x12 , x22 , x32 ,…}」(ただし、x12≠a2 , x22≠a2 , x32≠a2 ,… )
:
「収束数列{ x1n , x2n , x3n ,…}」(ただし、x1n ≠an , x2n ≠an , x3n ≠an ,… )
に対しても、
点列 { f ( Pi ) }={ f ( P1 ), f ( P2 ) , f ( P3 ) ,… }={ f ( x11,x12,…,x1n ) , f (x21,x22,…,x2n ), f (x31,x32,…,x3n ),… }
が収束する。 |
|
活用例 |
コーシーの判定法 |
|