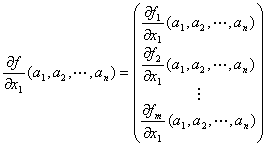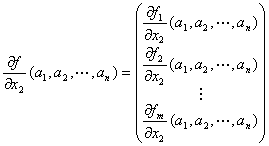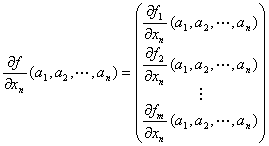|
|
[google adsense1:full] |
|
定義: (y1, y2, …,ym)=f (x1, x2, …,xn)は 点A=(a1, a2, …,an)においてxiについて偏微分可能 partially differentiable
点A=(a1, a2, …,an)におけるxiに関する偏微分係数 partially differential coefficient |
|
定義
|
(1)
・「 n変数m値ベクトル値関数( y1,y2,…,ym )=f ( x1,x2,…,xn) が
点(a1, a2, …,an)においてx1に関して偏微分可能partially differentiable」
とは、
x2,…,xnをそれぞれa2, …,anに固定して、x1だけの1変数m値ベクトル値関数とした
( y1,y2,…,ym )=f ( x1, a2, …,an )
が、
x1=a1において、x1について微分可能であること、
すなわち、
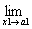 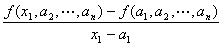
(この値は、実m次元数ベクトルとなる)
が収束すること
ないし、
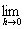 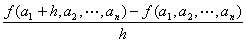
(この値は、実m次元数ベクトルとなる)
が収束すること
をいう。
* ここで、
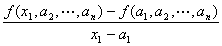
の右極限=右微分係数と左極限=左微分係数が
ともに存在して
一致することが含意されていることに注意。 |
[文献-数学]
・杉浦『解析入門』Ⅱ§3 (p.108).
・ルディン『現代解析学』9.13(p.210)
[文献-経済学]
・西村『経済学のための最適化理論入門』1.3.3(p.24)重要;
・神谷浦井『経済学のための数学入門』6.3.2 (p. 227)
※関連:
《n変数ベクトル値関数の微分可能・微分係数》の《1変数実数値関数の微分可能・微分係数》への還元
cf.1変数関数の微分係数/2変数関数の偏微分
|
| |
・「
点(a1, a2, …,an)における n変数m値ベクトル値関数( y1,y2,…,ym )=f ( x1,x2,…,xn) の
x1に関する偏微分係数partially differential coefficient・第1偏微係数」
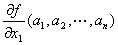
とは、
x2,…,xnをそれぞれa2, …,anに固定して、x1だけの1変数m値ベクトル値関数とした
( y1,y2,…,ym )= f ( x1 , a2, …,an )
の、
x1=a1における微分係数
すなわち、
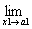 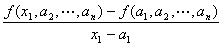
ないし、
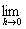 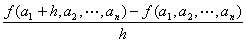
のことをいう。
(2)
・「 n変数m値ベクトル値関数( y1,y2,…,ym )=f ( x1,x2,…,xn) が
点(a1, a2, a3, …,an)においてx2に関して偏微分可能partially differentiable」
とは、
x1,x3,…,xnをそれぞれa1, a3, …,anに固定して、x2だけの1変数m値ベクトル値関数とした
( y1,y2,…,ym )=f ( a1 , x2, a3 ,…,an )
が、
x2=a2において、x2について微分可能あること、
すなわち、
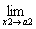 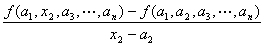
(この値は、実m次元数ベクトルとなる)
が収束すること
ないし、
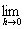 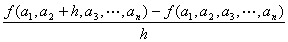
(この値は、実m次元数ベクトルとなる)
が収束すること
をいう。
*ここで、
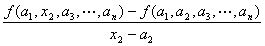
の右極限=右微分係数と左極限=左微分係数が
ともに存在して
一致することが含意されていることに注意。
・「点(a1, a2, a3, …,an)における n変数m値ベクトル値関数( y1,y2,…,ym )=f ( x1,x2,…,xn)の
x2に関する偏微分係数partially differential coefficient・第2偏微係数」
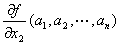
とは、
x1,x3,…,xnをそれぞれa1, a3, …,anに固定して、x2だけの1変数m値ベクトル値関数とした
( y1,y2,…,ym )= f ( a1, x2 , a3, …,an )
の、
x2=a2における微分係数
すなわち、
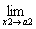 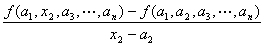
ないし、
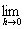 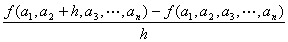
のことをいう。 |
[yahoo:tate]
|
| |
: |
|
| |
(n)
・「 n変数m値ベクトル値関数( y1,y2,…,ym )=f ( x1,x2,…,xn) が
点(a1, a2, …,an)においてxnに関して偏微分可能partially differentiable」
とは、
x1,x2,…,xn-1をそれぞれa1, a2, …,an-1に固定して、xnだけの1変数m値ベクトル値関数とした
( y1,y2,…,ym )=f ( a1 , a2 ,…, an-1 , xn )
が、
xn =anにおいて、xnについて微分可能あること、
すなわち、
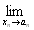 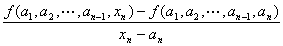
(この値は、実m次元数ベクトルとなる)
が収束すること
ないし、
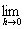 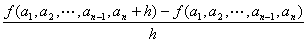
(この値は、実m次元数ベクトルとなる)
が収束すること
をいう。
*ここで、
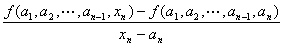
の右極限=右微分係数と左極限=左微分係数が
ともに存在して
一致することが含意されていることに注意。
・「点(a1, a2, …,an)における n変数m値ベクトル値関数( y1,y2,…,ym )=f ( x1,x2,…,xn)の
x nに関する偏微分係数partially differential coefficient・第n偏微係数」
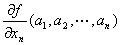
とは、
x1,x2,…,xn-1をそれぞれa1, a2, …,an-1に固定して、xnだけの1変数m値ベクトル値関数とした
( y1,y2,…,ym )=f ( a1 , a2 ,…, an-1 , xn )
の、
xn =anにおける微分係数
すなわち、
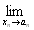 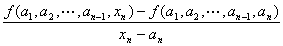
(この値は、実m次元数ベクトルとなる)
ないし、
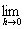 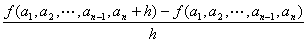
(この値は、実m次元数ベクトルとなる)
のことをいう。 |
[YouTube:tate] |
| |
|
|
| |
|
定理: n変数ベクトル値関数の微分可能・微分係数の、n変数実数値関数の微分可能・微分係数への還元 |
| |
n変数m値ベクトル値関数( y1,y2,…,ym )=f ( x1,x2,…,xn) が、
m個の n変数実数値関数 の組
y1=f1 (x1,x2,…,xn)
y2=f2 (x1,x2,…,xn)
: :
ym=fm (x1,x2,…,xn)
として表されるとする。
つまり、
( y1,y2,…,ym )=( f1 (x1,x2,…,xn), f2 (x1,x2,…,xn),…, fm (x1,x2,…,xn) )=f ( x1,x2,…,xn) |
[文献]
・加藤『微分積分学原論』16.2(p.196) |
|
(1) |
・以下の命題P,命題Qは同値。
命題P:
( y1,y2,…,ym )=f ( x1,x2,…,xn)は点(a1, a2, …,an) においてx1に関して偏微分可能
命題Q:
n変数実数値関数y1 =f1 (x1,x2,…,xn) は、x1に関して偏微分可能。
かつ
n変数実数値関数y2 =f2 (x1,x2,…,xn) は、x1に関して偏微分可能。
かつ
:
:
かつ
n変数実数値関数ym =fm (x1,x2,…,xn) は、x1に関して偏微分可能。
・ 上記の命題P,命題Qが成り立つならば、
「点(a1, a2, …,an)における( y1,y2,…,ym )=f ( x1,x2,…,xn)のx 1に関する偏微分係数」
は、
点(a1, a2, …,an)における n変数実数値関数f1, f2,…, fmのx 1に関する偏微分係数を並べた実m次元数ベクトル
に等しい。
つまり、命題P,命題Qが成り立つならば、
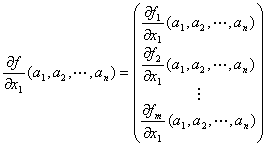
|
|
|
(2) |
・以下の命題P,命題Qは同値。
命題P:
( y1,y2,…,ym )=f ( x1,x2,…,xn)は点(a1, a2, …,an)においてx2に関して偏微分可能
命題Q:
n変数実数値関数y1 =f1 (x1,x2,…,xn) は、x2に関して偏微分可能。
かつ
n変数実数値関数y2 =f2 (x1,x2,…,xn) は、x2に関して偏微分可能。
かつ
:
:
かつ
n変数実数値関数ym =fm (x1,x2,…,xn) は、x2に関して偏微分可能。
・ 上記の命題P,命題Qが成り立つならば、
「点(a1, a2, …,an)における( y1,y2,…,ym )=f ( x1,x2,…,xn)のx 2に関する偏微分係数」
は、
点(a1, a2, …,an)における n変数実数値関数f1, f2,…, fmのx2に関する偏微分係数を並べた実m次元数ベクトル
に等しい。
つまり、命題P,命題Qが成り立つならば、
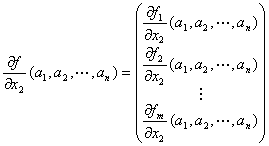
|
|
: |
: |
|
|
(n) |
・以下の命題P,命題Qは同値。
命題P:
( y1,y2,…,ym )=f ( x1,x2,…,xn)は点(a1, a2, …,an)においてxnに関して偏微分可能
命題Q:
n変数実数値関数y1 =f1 (x1,x2,…,xn) は、xnに関して偏微分可能。
かつ
n変数実数値関数y2 =f2 (x1,x2,…,xn) は、xnに関して偏微分可能。
かつ
:
:
かつ
n変数実数値関数ym =fm (x1,x2,…,xn) は、xnに関して偏微分可能。
・ 上記の命題P,命題Qが成り立つならば、
「点(a1, a2, …,an)における( y1,y2,…,ym )=f ( x1,x2,…,xn)のxnに関する偏微分係数」
は、
点(a1, a2, …,an)における n変数実数値関数f1, f2,…, fmのxnに関する偏微分係数を並べた実m次元数ベクトル
に等しい。
つまり、命題P,命題Qが成り立つならば、
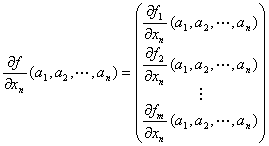
|
| |
|
|
|
なぜ?
|
[命題P⇔命題Q]
・命題P「 n変数m値ベクトル値関数( y1,y2,…,ym )=( f1 (x1,x2,…,xn), f2 (x1,x2,…,xn),…, fm (x1,x2,…,xn) )=f ( x1,x2,…,xn) が、点(a1, a2, …,an)においてx1に関して偏微分可能」
⇔命題P'「x2,…,xnをそれぞれa2, …,anに固定して、x1だけの1変数m値ベクトル値関数とした( y1,y2,…,ym )=f ( x1, a2, …,an )が、
x1=a1において、x1について微分可能であること」
∵ n変数m値ベクトル値関数が (a1, a2, …,an)においてx1に関して偏微分可能の定義
⇔命題P''
「・x2,…,xnをそれぞれa2, …,anに固定して、x1だけの1変数実数値関数としたy1=f1 ( x1, a2, …,an ) がx1=a1において微分可能
かつ
・x2,…,xnをそれぞれa2, …,anに固定して、x1だけの1変数実数値関数としたy2=f2 ( x1, a2, …,an ) がx1=a1において微分可能
かつ
:
かつ
・x2,…,xnをそれぞれa2, …,anに固定して、x1だけの1変数実数値関数としたy m=f m ( x1, a2, …,an ) がx1=a1において微分可能 」
∵1変数ベクトル値関数の微分可能性の、1変数実数値関数の微分可能性、への還元にしたがって、命題P'を書き下した。
⇔命題Q
「 n変数実数値関数y1 =f1 (x1,x2,…,xn) は、点(a1, a2, …,an)でx1に関して偏微分可能。
かつ
n変数実数値関数y2 =f2 (x1,x2,…,xn) は、点(a1, a2, …,an)でx1に関して偏微分可能。
かつ
:
:
かつ
n変数実数値関数ym =fm (x1,x2,…,xn) は、点(a1, a2, …,an)でx1に関して偏微分可能。 」
∵ n変数実数値関数の偏微分可能の定義
[ 偏微分係数]
「点(a1, a2, …,an)における( y1,y2,…,ym )=( f1 (x1,x2,…,xn), f2 (x1,x2,…,xn),…, fm (x1,x2,…,xn) )=f ( x1,x2,…,xn)のx 1に関する偏微分係数」
とは、
「x2,…,xnをそれぞれa2, …,anに固定して、x1だけの1変数m値ベクトル値関数とした( y1,y2,…,ym )= f ( x1, a2, …,an )の、x1=a1における微分係数」
のことであり、 ∵ n変数m値ベクトル値関数の (a1, a2, …,an)におけるx1に関する偏微分係数の定義
これは、
「・x2,…,xnをそれぞれa2, …,anに固定して、x1だけの1変数実数値関数としたy1=f1 ( x1, a2, …,an ) のx1=a1における微分係数
・x2,…,xnをそれぞれa2, …,anに固定して、x1だけの1変数実数値関数としたy2=f2 ( x1, a2, …,an ) のx1=a1における微分係数
:
・x2,…,xnをそれぞれa2, …,anに固定して、x1だけの1変数実数値関数としたy m=f m ( x1, a2, …,an ) のx1=a1における微分係数
を並べた実m次元数ベクトル 」
のことであり、 ∵1変数ベクトル値関数の微分可能性の、1変数実数値関数の微分可能性、への還元
さらに、これは、
「 n変数実数値関数y1 =f1 (x1,x2,…,xn) は、点(a1, a2, …,an)でx1に関して偏微分係数。
かつ
n変数実数値関数y2 =f2 (x1,x2,…,xn) は、点(a1, a2, …,an)でx1に関して偏微分係数。
かつ
:
:
かつ
n変数実数値関数ym =fm (x1,x2,…,xn) は、点(a1, a2, …,an)でx1に関して偏微分係数。 」
のことに他ならない。 ∵ n変数実数値関数の偏微分係数の定義 |
| |
|
|
定義:ベクトル値関数の偏導関数 partial derivative |
|
定義
|
(1)「 n変数m値ベクトル値関数( y1,y2,…,ym )=f ( x1,x2,…,xn)の
x1に関する偏導関数partially derivative」とは?
( y1,y2,…,ym )=f ( x1,x2,…,xn)が各点で、x1に関して偏微分可能であるとき、
定点(a1, a2, …,an)におけるx1に関する偏微分係数
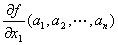 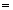 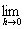 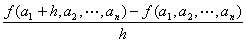
の値(実m次元数ベクトルとなる)は、
定点(a1, a2, …,an)のとりかたによって変わってくるから、
定点(a1, a2, …,an)の n変数m値ベクトル値関数。
定点(a1, a2, …,an)を動点(x1, x2, …,xn)として書き改めた n変数m値ベクトル値関数
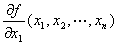 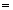 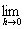 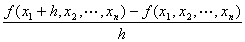
を、
n変数m値ベクトル値関数( y1,y2,…,ym )=f ( x1,x2,…,xn)の
x1に関する偏導関数・第1偏導関数と呼ぶ。
(2) 「 n変数m値ベクトル値関数( y1,y2,…,ym )=f ( x1,x2,…,xn)の
x2に関する偏導関数partially derivative」とは?
( y1,y2,…,ym )=f ( x1,x2,…,xn)が各点で、x2に関して偏微分可能であるとき、
定点(a1, a2, a3, …,an)におけるx2に関する偏微分係数
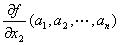 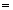 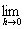 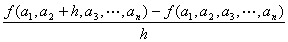
の値(実m次元数ベクトルとなる)は、
定点(a1, a2, a3, …,an)のとりかたによって変わってくるから、
定点(a1, a2, a3, …,an)の n変数m値ベクトル値関数。
定点(a1, a2, …,an)を動点(x1, x2, …,xn)として書き改めた n変数m値ベクトル値関数
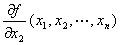 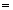 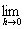 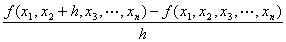
を、
n変数m値ベクトル値関数( y1,y2,…,ym )=f ( x1,x2,…,xn)の
x2に関する偏導関数・第2偏導関数と呼ぶ。
:
:
:
(n) 「 n変数m値ベクトル値関数( y1,y2,…,ym )=f ( x1,x2,…,xn)の
xnに関する偏導関数partially derivative」とは?
( y1,y2,…,ym )=f ( x1,x2,…,xn)が各点で、xnに関して偏微分可能であるとき、
定点(a1, a2, …, an-1, an)におけるxnに関する偏微分係数
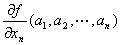 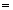 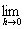 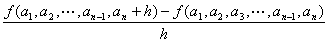
の値(実m次元数ベクトルとなる)は、
定点(a1, a2, …, an-1, an)のとりかたによって変わってくるから、
定点(a1, a2, …, an-1, an)の n変数m値ベクトル値関数。
定点(a1, a2, …, an-1, an)を動点(x1, x2, …,xn-1,xn)として書き改めた n変数m値ベクトル値関数
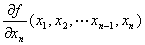 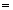 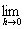 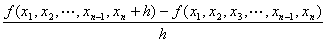
を、
n変数m値ベクトル値関数( y1,y2,…,ym )=f ( x1,x2,…,xn)の
xnに関する偏導関数・第n偏導関数と呼ぶ。 |
[文献]
・杉浦『解析入門』Ⅱ§3 (p.108).
[文献-経済学]
・西村『経済学のための最適化理論入門』1.3.3(p.24)重要;
・神谷浦井『経済学のための数学入門』6.3.2 (p. 227)
cf.1変数関数の微分係数/2変数関数の偏微分
cf. |
|
記法 |
(1) n変数m値ベクトル値関数( y1,y2,…,ym )= f ( x1,x2,…,xn)のx1に関する偏導関数は、
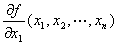 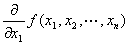
∂f/∂x1 ∂y /∂x1
fx1 (x1,x2,…,xn) Dx1 f ( x1,x2,…,xn) D1 f ( x1,x2,…,xn)
等の記号で表される。
(2) n変数m値ベクトル値関数( y1,y2,…,ym )= f ( x1,x2,…,xn)のx2に関する偏導関数は、
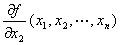 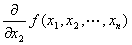
∂f /∂x2 ∂y /∂x2
fx2 (x1,x2,…,xn) Dx2 f ( x1,x2,…,xn) D2 f ( x1,x2,…,xn)
等の記号で表される。
:
:
:
(n) n変数m値ベクトル値関数( y1,y2,…,ym )= f ( x1,x2,…,xn)のxnに関する偏導関数は、
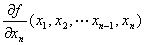 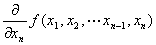
∂f/∂xn ∂y /∂xn
fxn (x1,x2,…,xn) Dxnf ( x1,x2,…,xn) Dnf ( x1,x2,…,xn)
等の記号で表される。 |
* 記号の読み方
・∂は、「丸いd」「ラウンドデルタ」「ラウンドディ」等と呼ばれる。
・∂f /∂x1は、「デルf デルx1 」等と読む。
[小形『多変数の微分積分』p.22]
[入谷久我『数理経済学入門』定義7.1(p.163)]
[小島寛之『ゼロから学ぶ微分積分』fs.129] |
|
活用 |
・ ヤコビ行列: n変数m値ベクトル値関数( y1,y2,…,ym )= f ( x1,x2,…,xn)のn個の偏導関数を、それぞれ縦ベクトルで表した上で、横に並べて作った行列。 |
|
※ |
偏微分可能から 連続性は出てこない。
→ 1変数関数の微分可能性と連続性
→ n変数関数の全微分可能性
→ n変数関数の連続性 |
|
| |
|
|
定義:ベクトル値関数の連続微分可能・ C1級 |
|
定義
|
「
n変数m値ベクトル値関数( y1,y2,…,ym )= f ( x1,x2,…,xn)が連続微分可能」
「 n変数m値ベクトル値関数( y1,y2,…,ym )= f ( x1,x2,…,xn)がC1級」とは、
・( y1,y2,…,ym )= f ( x1,x2,…,xn)が各点でx1,x2,…,xnの各々に関して偏微分可能で
x1,x2,…,xnの各々に関する偏導関数
∂f /∂x1 (x1,x2,…,xn) , ∂f /∂x2(x1,x2,…,xn), … , ∂f /∂xn(x1,x2,…,xn)
がすべて存在し、
かつ、
・x1,x2,…,xnの各々に関する( y1,y2,…,ym )= f ( x1,x2,…,xn)の偏導関数
∂f /∂x1 (x1,x2,…,xn), ∂f /∂x2 (x1,x2,…,xn), … ,∂f /∂xn (x1,x2,…,xn)
がすべて連続関数であるということ
をいう。 |
[文献-数学]
・杉浦『解析入門』Ⅱ§3 定義4(p.111)。
※以下の文献は、
この定義の必要十分条件のほうを、
連続微分可能(C1級)の定義としている。
・松坂『解析入門4』17.1C (p.63).
・ルディン『現代解析学』9.15(p.211)
|
|
類概念 |
1変数関数の連続微分可能性、1変数関数のCn級、
2変数関数のCn級 |
|
| |
|
|
定理:ベクトル値関数が連続微分可能であるための必要十分条件 |
|
定理
|
次の命題
P,命題Q,命題Rは同値。
命題P:
「 n変数m値ベクトル値関数( y1,y2,…,ym )= f ( x1,x2,…,xn)が連続微分可能(C1級)」
命題Q:
「 n変数m値ベクトル値関数( y1,y2,…,ym )= f ( x1,x2,…,xn)が微分可能
かつ
n変数m値ベクトル値関数( y1,y2,…,ym )= f ( x1,x2,…,xn)の導関数が連続」
(ベクトル値関数の導関数の連続性の定義は、ルディンに出ている)
(松坂『解析入門4』問題15.2-2 (p.27)も参照)
命題R:
n変数m値ベクトル値関数( y1,y2,…,ym )=f ( x1,x2,…,xn) を、
m個の n変数実数値関数 の組
y1=f1 (x1,x2,…,xn)
y2=f2 (x1,x2,…,xn)
: :
ym=fm (x1,x2,…,xn)
として表す、
つまり、
( y1,y2,…,ym )=( f1 (x1,x2,…,xn), f2 (x1,x2,…,xn),…, fm (x1,x2,…,xn) )=f ( x1,x2,…,xn)
として表すと、
「 n変数実数値関数y1 =f1 (x1,x2,…,xn) がC1級
かつ
y2=f2 (x1,x2,…,xn) がC1級
かつ
:
かつ
ym=fm (x1,x2,…,xn) がC1級」
|
[文献-数学]
・ルディン『現代解析学』9.16(p.211)
・杉浦『解析入門』Ⅱ§6命題6.3(p.130).
・松坂『解析入門4』17.1C命題4 (p.63).
|
|
類概念 |
|
|
| |
|