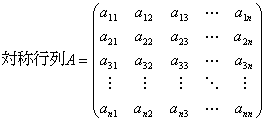n変数二次形式　quadratic form　

　・定義：二次形式/正値定符号二次形式/正値定符号行列/半正値定符号二次形式/半正値定符号行列
　　　　　負値定符号二次形式/負値定符号行列/半負値定符号二次形式/半負値定符号行列 /不定符号二次形式　
　　　　　同値な二次形式/二次形式の標準形　　
　・定理：単位ベクトル化の二次形式の計算／単位ベクトル化の二次形式の最大値・最小値定理
　　　　　二次形式の基底変換公式/二次形式の標準化　　　　　　　　　　　　　　　　　　　
　　　　　正値定の必要十分条件-固有値/負値定の必要十分条件-固有値/正値定の必要条件-行列式/負値定の必要条件-行列式/
　　　　　正値定の必要条件-小行列/負値定の必要条件-小行列/正値定の必要十分条件-主小行列式/負値定の必要十分条件-主小行列式

※応用：n変数関数の極値問題　
※具体例：2変数の二次形式　
※関連：主小行列/主小行列式/固有値　
→線形代数目次/総目次　

定義：二次形式 quadratic form

→[定義/Σの表現/行列表現/内積表現]
 ※具体例→2変数の二次形式


定義


・「n個の変数x1, x2, x3, …, xnについての二次形式」とは、
　n個の変数x1, x2, x3, …, xnについての多項式で、2次の項ばかりからなるもの　
　　すなわち、｢斉２次式｣・２次の｢同次多項式｣
　　Q (x1, x2, x3, …, xn) = c11x12+ c12 x1x2+ c13 x1x3+…+ c1n x1xn　
　　　　　　　　　　　　　　+ c22 x22+ c23x2x3+…+ c2n x2xn　
　　　　　　　　　　　　　　　　　　+ c33x32+ c34x3x4+…+ c3n x3xn　
　　　　　　　　　　　　　　　　　　　+…
　　　　　　　　　　　　　　　　　　　　…+ cnn xn2　　　
　のことをいう。


[文献－線型代数]
・佐武『線型代数学』Ⅳ§4 (p.158)
・斎藤『線形代数入門』153;
・永田『理系のための線形代数の基礎142;
・川久保『線形代数学』11.3(pp.288-9)
・藤原『線形代数』152.
・木村『線形代数：数理科学の基礎』2.1(p.35)
[文献－解析]
＊杉浦『解析入門１』Ⅱ§8定義1(p.153)
＊松坂『解析入門3』14.3-A (p.168):行列を使わずに。
＊松坂『解析入門4』18.2-E (p.105):行列を用いて。
[文献－数理経済]
・岡田『経済学・経営学のための数学』2.7定理3.4(p.112)
・入谷久我『数理経済学入門』定義8.2 (p.188).
[文献－数理統計]
　・久米『数理統計学』1.33(p.32);
　
※性質：二次形式で定義された関数はRn上連続
※応用： n変数関数の極大の十分条件/ n変数関数の極小の十分条件　

Σの
表現

便宜上、
「n個の変数x1, x2, x3, …, xnについての二次形式」Q(x1, x2, x3, …, xn)を、
以下のように表す。
　　　・i=jについては、aij = cij　
　　　　　　　つまり、a11= c11, a22= c22,…, ann= cnn　　
　　　・i≠jについては、aij = ajj= cij /2　
　　　　　　　つまり、cij = aij + ajj= 2aij　　
　とおいて、
Q (x1, x2, x3, …, xn)
　
　= a11x12+ a12 x1x2+ a13 x1x3+…+ a1n x1xn　
　　+ a21x2x1+ a22 x22+ a23x2x3+…+ a2n x2xn　
　　+ a31x3x1+ a32x3x2+ a33x32+ a34x3x4+…+ a3n x3xn　
　　+…　　　　　　　　　
　　+ an1 xnx1+ an2xnx2+ an3xn x3 +…+ an(n-1) xn x(n-1) + ann xn2　
　　
　＝a11x12+ 2a12 x1x2+ 2a13 x1x3+…+ 2a1n x1xn　
　　　　+ a22 x22+ 2a23x2x3+…+ 2a2n x2xn　
　　　　　　　　+ a33x32+ 2a34x3x4+…+ 2a3n x3xn　
　　　　　　　　　+…
　　　　　　　　　　…+ 2ann xn2　　　

行列
表現

このような表し方をしておくと、
　「n個の変数x1, x2, x3, …, xnについての二次形式」Q(x1, x2, x3, …, xn)は
　　　
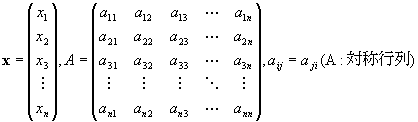
　をつかって、
　行列積 txAx　として表せる。
　実際、txAx　
　　　　　

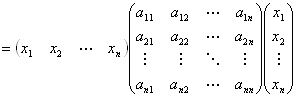
　　　　　＝(a11x1+a21x2+…+an1xn , a12x1+a22x2+…+an2xn,…, a1nx1+a2nx2+…+annxn)

　　　　= (a11x1+a21x2+…+an1xn )x1+(a12x1+a22x2+…+an2xn)x2+…+(a1nx1+a2nx2+…+annxn)xn
　　　　= a11x12+ a12 x1x2+ a13 x1x3+…+ a1n x1xn　
　　　　　+ a21x2x1+ a22 x22+ a23x2x3+…+ a2n x2xn　
　　　　　+…　　　　　　　　　
　　　　　+ an1 xnx1+ an2xnx2+ an3xn x3 +…+ an(n-1) xn x(n-1) + ann xn2　
　　　　＝a11x12+ 2a12 x1x2+ 2a13 x1x3+…+ 2a1n x1xn　
　　　　　　　　+ a22 x22+ 2a23x2x3+…+ 2a2n x2xn　
　　　　　　　　　　　+ a33x32+ 2a34x3x4+…+ 2a3n x3xn　
　　　　　　　　　　　　+…
　　　　　　　　　　　　　…+ 2ann xn2　　　　　　
　　　　= c11x12+ c12 x1x2+ c13 x1x3+…+ c1n x1xn　
　　　　　　　　　　　　　　+ c22 x22+ c23x2x3+…+ c2n x2xn　
　　　　　　　　　　　　　　　　　　+ c33x32+ c34x3x4+…+ c3n x3xn　
　　　　　　　　　　　　　　　　　　　+…
　　　　　　　　　　　　　　　　　　　　…+ cnn xn2　
　　　　=Q (x1, x2, x3, …, xn)　
※なお、
　対称行列Aの対角成分a11, a22, a33, …, annは、それぞれ、
　2次形式の2乗の項x12, x22, x32, …, xn2 の係数を表し、　
　対称行列Aの非対角成分は、2次形式の交叉項xi xj (i≠j)の係数を表している。
　だから、
　Aが対角行列であるならば、二次形式txAxは2乗の項のみからなっていると判断でき、
　Aが対角行列かつ全ての対角成分が正であるならば、　
　xの値にかかわらず、二次形式txAxは正値である（→正値定符号二次形式）
　と判断できる。
　　　　　　　
※「二次形式txAxの(係数)行列」といえば、対称行列Aのことを指す。
※「二次形式txAxの階数」といえば、対称行列Aの階数のことを指す。
※txAx　を、対称行列Aによって定まる二次形式という意味で、A[x]とも書く。

※2次形式は、x＝(x1, x2, x3, …, xn)の関数であって、Rn上で連続（∵）。

例

n=2のときの具体例：
2個の変数x1, x2についての2次の項ばかりからなる多項式を、
2個の変数x1, x2についての二次形式という。
以下のどちらも同じ2次形式を表すことを確認せよ。
　
　　＝a11x1x1+ a12x1x2+ a21x2x1+ a22x2x2　
　　＝a11x12+ 2 a12x1x2 + a22 x22　　　　　　　　∵a12＝a21　
　　
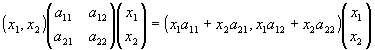
　　＝ (x1 a11+ x2 a21) x1 +(x1a12+ x2 a22) x2　
　　＝a11x12+ 2 a12x1x2 + a22 x22　　　　　　　　∵a12＝a21　
たとえば、二次形式3x12+ 7x1x2 + 5 x22　なら、　　　　　
　3x12+ 7x1x2 + 5 x22＝3x12+ 2・7/2 x1x2 + 5 x22　（つまり、a12＝7/2　として、）　
　　　＝3x12+7/2 x1x2 +7/2 x2x1 +5 x22　
　　　＝ (3x1 + 7/2 x2) x1 +(7/2 x1+ 5 x2) x2　
　　　　
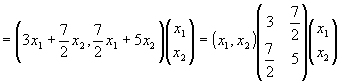
　　と表せる。　

 　

例

n=3のときの具体例：
3個の変数x1, x2, x3についての2次の項ばかりからなる多項式を、
3個の変数x1, x2, x3についての二次形式という。
以下のどちらも同じ2次形式を表すことを確認せよ。
　
　　＝a11x1x1+ a12x1x2+ a13x1x3+ a21x2x1+ a22x2x2+ a23x2x3+ a31x3x1+ a32x3x2+ a33x3x3
　　＝a11x12+ a22 x22+ a33x32+ 2 a12x1x2 + 2 a13x1x3 + 2 a23x2x3　∵a12＝a21、a13＝a31、a23＝a32　
　
　　　　
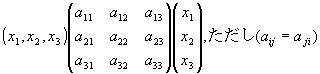
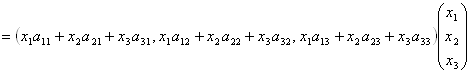
　　　＝ (x1 a11+ x2 a21+ x3 a31) x1 +(x1a12+ x2 a22+ x3 a32) x2+(x1a13+ x2 a23+ x3 a33) x3　
　　　＝a11x12+ a22 x22+ a33x32+ 2 a12x1x2 + 2 a13x1x3 + 2 a23x2x3　∵a12＝a21、a13＝a31、a23＝a32　

 　
内積表現
 「n個の変数x1, x2, x3, …, xnについての二次形式」Q(x1, x2, x3, …, xn)は、

　　　
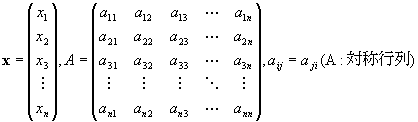
と自然な内積をつかって、
　　　x・Ax
ないし
　　　Ax・x
と表すことができる。

※

 　 　
　 　

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

 　

　

定義：正値定符号二次形式positive definite


行列を
用いない
定義


「『x1, x2, x3, …, xnについての二次形式』Q (x1, x2, x3, …, xn)は正値である」
「『x1, x2, x3, …, xnについての二次形式』Q (x1, x2, x3, …, xn)は正値定符号二次形式である」
「『x1, x2, x3, …, xnについての二次形式』Q (x1, x2, x3, …, xn)は正定形式positive formである」
とは、
　x1=x2=…=xn=０ではない限りで任意の(x1, x2, …, xn)に対して、
　　『x1, x2, x3, …, xnについての二次形式』Q (x1, x2, x3, …, xn)>０　
　が成り立つことをいう。

　→　正値定符号行列　　

※具体例→2変数の正値定符号二次 形式
　　
[文献－線型代数]
・佐武『線型代数学』Ⅳ§4 (p.161)
・斎藤『線形代数入門』155;
・永田『理系のための線形代数の基礎』149;
・木村『線形代数：数理科学の基礎』2.1(p.36):平方完成との関連。

[文献－解析]
＊杉浦『解析入門１』Ⅱ§8定義1(p.153)
＊松坂『解析入門3』14.3-A (p.169):行列を使わずに。
＊松坂『解析入門4』18.2-E (p.107):行列を用いて。

[文献－数理経済]
・入谷久我『数理経済学入門』定義8.2 (p.188).
・Chiang, Fundamental Methods of Mathematiaal Economics, 320.
・岩田『経済分析のための統計的方法』311


行列を
用いた
定義


「二次形式txAxは正値である」
「二次形式txAxは正値定符号二次形式である」
「二次形式txAxは正定形式positive formである」
とは、
　零ベクトルでない任意の実n次元数ベクトルxに対して
　　　　　二次形式 txAx >０　
　が成り立つことをいう。

　→　正値定符号行列　　

※

簡単なかたちの２次形式ならば、
平方完成によって、正値定符号の判定が可能。
複雑な場合は、どのようにして、正値定符号の判定を行うか？
→固有値による正値定符号の判定
→主小行列式による正値定符号の判定
　 　

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

 　

定義：正値定符号行列positive definite matrix


1.


正値定符号行列・正定行列とは、
正値定符号二次形式Q (x1, x2, x3, …, xn)を txAxというかたちに表した際の
対称行列Aのことをいう。

 ※具体例→2×2正値定符号行列　


2.


具体的にいえば、
Q (x1, x2, x3, …, xn) = c11x12+ c12 x1x2+ c13 x1x3+…+ c1n x1xn　
　　　　　　　　　　　　　　+ c22 x22+ c23x2x3+…+ c2n x2xn　
　　　　　　　　　　　　　　　　　　+ c33x32+ c34x3x4+…+ c3n x3xn　
　　　　　　　　　　　　　　　　　　　+…
　　　　　　　　　　　　　　　　　　　　…+ cnn xn2　　　
が正値定符号二次形式であるとき、
　　　・i=jについては、aij = cij　
　　　　　　　つまり、a11= c11, a22= c22,…, ann= cnn　　
　　　・i≠jについては、aij = ajj= cij /2　
　　　　　　　つまり、cij = aij + ajj= 2aij　　
とおいて作成した
　　　
を正値定符号行列と呼ぶ。


[文献－線型代数]
・佐武『線型代数学』Ⅳ§4 (p.161)
・斎藤『線形代数入門』155;
・永田『理系のための線形代数の基礎』149;
・木村『線形代数：数理科学の基礎』2.3(p.39)。

[文献－解析]
＊杉浦『解析入門１』Ⅱ§8定義1(p.153)
＊松坂『解析入門3』14.3-A (p.169):行列を使わずに。
＊松坂『解析入門4』18.2-E (p.107):行列を用いて。

[文献－数理経済]
・岡田『経済学・経営学のための数学』2.7 (p.113)
[文献－数理統計]
・久米『数理統計学』1.34(p.33);
・岩田『経済分析のための統計的方法』311
・Greene , Econometric Analysis,46.


3.


要するに、
「行列Aは正値定符号行列である」
「行列Aは正定行列である」
　とは、
　Aによって定まる二次形式txAxが正値定符号二次形式となること
　　　つまり、零ベクトルでない任意の実n次元数ベクトルxに対して、txAx >０となること
　である。　

　→正値定符号二次形式

 　

※

簡単なかたちの２次形式ならば、
平方完成によって、正値定符号の判定が可能。
複雑な場合は、どのようにして、正値定符号の判定を行うか？
→固有値による正値定符号の判定
→主小行列式による正値定符号の判定
　 　

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

 　

定義：半正値定符号二次形式positive semi-definite


行列を
用いない
定義


「『x1, x2, x3, …, xnについての二次形式』Q (x1, x2, x3, …, xn)は半正値である」
「『x1, x2, x3, …, xnについての二次形式』Q (x1, x2, x3, …, xn)は半正値定符号二次形式である」
とは、
　x1=x2=…=xn=０ではない限りで任意の(x1, x2, …, xn)に対して、
　　『x1, x2, x3, …, xnについての二次形式』Q (x1, x2, x3, …, xn)≧０　
　が成り立つことをいう。

　→　半正値定符号行列　　

※具体例→2変数の半正値定符号二次形式
　
[文献－線型代数]
・佐武『線型代数学』Ⅳ§4 (p.161)
・斎藤『線形代数入門』155;
・永田『理系のための線形代数の基礎』149;

[文献－解析]
＊杉浦『解析入門１』Ⅱ§8定義1(p.153)
＊松坂『解析入門3』14.3-A (p.169):行列を使わずに。
＊松坂『解析入門4』18.2-E (p.107):行列を用いて。

[文献－数理経済]
・入谷久我『数理経済学入門』定義8.2 (p.188).
・Chiang, Fundamental Methods of Mathematiaal Economics, 320.
・岩田『経済分析のための統計的方法』311


行列を
用いた
定義


「二次形式txAxは半正値である」
「二次形式txAxは半正値定符号二次形式である」
とは、
　零ベクトルでない任意の実n次元数ベクトルxに対して　
　　　二次形式 txAx ≧０　
　が成り立つことをいう。

　→　半正値定符号行列　　
　 　 　

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

 　

　

定義：半正値定符号行列positive semi-definite matrix , 非負値定符号行列non-negative difinite matrix


1.


半正値定符号行列・半正定行列・非負値符号行列・非負定行列とは、
半正値定符号二次形式Q (x1, x2, x3, …, xn)を txAxというかたちに表した際の
対称行列Aのことをいう。

※具体例→2行2列の半正値定符号行列　

[文献－線型代数]
・佐武『線型代数学』Ⅳ§4 (p.161)
・斎藤『線形代数入門』155;
・永田『理系のための線形代数の基礎』149;
・木村『線形代数：数理科学の基礎』2.3(p.39)。「半正定」「非負定」

[文献－解析]
＊杉浦『解析入門１』Ⅱ§8定義1(p.153)
＊松坂『解析入門3』14.3-A (p.169):行列を使わずに。
＊松坂『解析入門4』18.2-E (p.107):行列を用いて。

[文献－数理経済]
・岡田『経済学・経営学のための数学』2.7 (p.113)


[文献－数理統計]
・久米『数理統計学』1.34(p.33);
・岩田『経済分析のための統計的方法』311
・Greene , Econometric Analysis,46.


2.


具体的にいえば、
Q (x1, x2, x3, …, xn) = c11x12+ c12 x1x2+ c13 x1x3+…+ c1n x1xn　
　　　　　　　　　　　　　　+ c22 x22+ c23x2x3+…+ c2n x2xn　
　　　　　　　　　　　　　　　　　　+ c33x32+ c34x3x4+…+ c3n x3xn　
　　　　　　　　　　　　　　　　　　　+…
　　　　　　　　　　　　　　　　　　　　…+ cnn xn2　　　
が半正値定符号二次形式であるとき、
　　　・i=jについては、aij = cij　
　　　　　　　つまり、a11= c11, a22= c22,…, ann= cnn　　
　　　・i≠jについては、aij = ajj= cij /2　
　　　　　　　つまり、cij = aij + ajj= 2aij　　
とおいて作成した
　　　
を半正値定符号行列と呼ぶ。


要するに、
3.


「行列Aは半正値定符号行列である」
「行列Aは半正定行列である」
「行列Aは非負値符号行列である」
「行列Aは非負定行列である」
とは、
Aによって定まる二次形式txAxが半正値定符号二次形式となること
　　　つまり、零ベクトルでない任意の実n次元数ベクトルxに対して、txAx ≧０となること
である。　
　→　半正値定符号二次形式

※

 　 　

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

 　

　

定義：負値定符号二次形式 negative definite


行列を
用いない
定義


「『x1, x2, x3, …, xnについての二次形式』Q (x1, x2, x3, …, xn)は負値である」
「『x1, x2, x3, …, xnについての二次形式』Q (x1, x2, x3, …, xn)は負値定符号二次形式である」
とは、
　x1=x2=…=xn=０ではない限りで任意の(x1, x2, …, xn)に対して、
　　『x1, x2, x3, …, xnについての二次形式』Q (x1, x2, x3, …, xn)<０　
　が成り立つことをいう。

　→負値定符号行列　　　

※具体例→2変数の負値定符号二次形式　

[文献－線型代数]
・佐武『線型代数学』Ⅳ§4 (p.161)
・斎藤『線形代数入門』155;
・永田『理系のための線形代数の基礎』149;

[文献－解析]
＊杉浦『解析入門１』Ⅱ§8定義1(p.153)
＊松坂『解析入門3』14.3-A (p.169):行列を使わずに。
＊『解析入門4』18.2-E (p.107):行列を用いて。

[文献－数理経済]
・入谷久我『数理経済学入門』定義8.2 (p.188).
・Chiang, Fundamental Methods of Mathematiaal Economics, 320.
・岩田『経済分析のための統計的方法』311


行列を
用いた
定義


「二次形式txAxは負値である」
「二次形式txAxは負値定符号二次形式である」
とは、
　(０, ０,…, ０)ではない任意の(x1, x2, …, xn)に対して、
　　　　すなわち、零ベクトルでない任意の実n次元数ベクトルxに対して　
　二次形式 txAx ＜０　が成り立つことをいう。

　→　負値定符号行列　　

※

 　 　

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

 　

　

定義：負値定符号行列negative definite matrix


1.


負値定符号行列・負定行列とは、
負値定符号二次形式Q (x1, x2, x3, …, xn)を txAxというかたちに表した際の
対称行列Aのことをいう。

※具体例→2行2列の負値定符号行列　

[文献－線型代数]
・佐武『線型代数学』Ⅳ§4 (p.161)
・斎藤『線形代数入門』155;
・永田『理系のための線形代数の基礎』149;

[文献－解析]
＊杉浦『解析入門１』Ⅱ§8定義1(p.153)
＊松坂『解析入門3』14.3-A (p.169):行列を使わずに。
＊松坂『解析入門4』18.2-E (p.107):行列を用いて。

[文献－数理経済]
・岡田『経済学・経営学のための数学』2.7 (p.113)


[文献－数理統計]
・岩田『経済分析のための統計的方法』311
・Greene , Econometric Analysis,46.


2.


具体的にいえば、
Q (x1, x2, x3, …, xn) = c11x12+ c12 x1x2+ c13 x1x3+…+ c1n x1xn　
　　　　　　　　　　　　　　+ c22 x22+ c23x2x3+…+ c2n x2xn　
　　　　　　　　　　　　　　　　　　+ c33x32+ c34x3x4+…+ c3n x3xn　
　　　　　　　　　　　　　　　　　　　+…
　　　　　　　　　　　　　　　　　　　　…+ cnn xn2　　　
が負値定符号二次形式であるとき、
　　　・i=jについては、aij = cij　
　　　　　　　つまり、a11= c11, a22= c22,…, ann= cnn　　
　　　・i≠jについては、aij = ajj= cij /2　
　　　　　　　つまり、cij = aij + ajj= 2aij　　
とおいて作成した
　　　
を負値定符号行列と呼ぶ。


3.


要するに、
「行列Aは負値定符号行列である」
「行列Aは負定行列である」
　とは、
　Aによって定まる二次形式txAxが負値定符号二次形式となること
　　　つまり、零ベクトルでない任意の実n次元数ベクトルxに対して、txAx ＜０となること
　である。　

　→　負値定符号二次形式

※

 　 　

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

 　

定義：半負値定符号二次形式 negative semidefinite


行列を
用いない
定義


「『x1, x2, x3, …, xnについての二次形式』Q (x1, x2, x3, …, xn)は半負値である」
「『x1, x2, x3, …, xnについての二次形式』Q (x1, x2, x3, …, xn)は半負値定符号二次形式である」
とは、
　x1=x2=…=xn=０ではない限りで任意の(x1, x2, …, xn)に対して、
　　『x1, x2, x3, …, xnについての二次形式』Q (x1, x2, x3, …, xn) ≦０　
　が成り立つことをいう。

　→　半負値定符号行列　　

※具体例→2変数の半負値定符号二次形式　

[文献－線型代数]
・佐武『線型代数学』Ⅳ§4 (p.161)
・斎藤『線形代数入門』155;
・永田『理系のための線形代数の基礎』149;

[文献－解析]
＊杉浦『解析入門１』Ⅱ§8定義1(p.153)
＊松坂『解析入門3』14.3-A (p.169):行列を使わずに。
＊松坂『解析入門4』18.2-E (p.107):行列を用いて。

[文献－数理経済]
・入谷久我『数理経済学入門』定義8.2 (p.188).
・Chiang, Fundamental Methods of Mathematiaal Economics, 320.
・岩田『経済分析のための統計的方法』311


行列を
用いた
定義


「二次形式txAxは半負値である」
「二次形式txAxは半負値定符号二次形式である」
とは、
　零ベクトルでない任意の実n次元数ベクトルxに対して　
　　　　　　二次形式 txAx ≦０　
　が成り立つことをいう。

　→　半負値定符号行列　　　

※

 　 　

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

 　

　

定義：半負値定符号行列negative semi-definite matrix , 非正値定符号行列non-positive difinite matrix


1.


半負値定符号行列・非正値定符号行列とは、
半負値定符号二次形式Q (x1, x2, x3, …, xn)を txAxというかたちに表した際の
対称行列Aのことをいう。　

※具体例→2行2列の半負値定符号行列 　

[文献－線型代数]
・佐武『線型代数学』Ⅳ§4 (p.161)
・斎藤『線形代数入門』155;
・永田『理系のための線形代数の基礎』149;

[文献－解析]
＊杉浦『解析入門１』Ⅱ§8定義1(p.153)
＊松坂『解析入門3』14.3-A (p.169):行列を使わずに。
＊松坂『解析入門4』18.2-E (p.107):行列を用いて。

[文献－数理経済]
・岡田『経済学・経営学のための数学』2.7 (p.113)
・岩田『経済分析のための統計的方法』311
・Greene , Econometric Analysis,46.


2.


具体的にいえば、
Q (x1, x2, x3, …, xn) = c11x12+ c12 x1x2+ c13 x1x3+…+ c1n x1xn　
　　　　　　　　　　　　　　+ c22 x22+ c23x2x3+…+ c2n x2xn　
　　　　　　　　　　　　　　　　　　+ c33x32+ c34x3x4+…+ c3n x3xn　
　　　　　　　　　　　　　　　　　　　+…
　　　　　　　　　　　　　　　　　　　　…+ cnn xn2　　　
が半負値定符号二次形式であるとき、
　　　・i=jについては、aij = cij　
　　　　　　　つまり、a11= c11, a22= c22,…, ann= cnn　　
　　　・i≠jについては、aij = ajj= cij /2　
　　　　　　　つまり、cij = aij + ajj= 2aij　　
とおいて作成した
　　　
を半負値定符号行列・非正値定符号行列と呼ぶ。


3.


要するに、
「行列Aは半負値定符号行列である」
「行列Aは非正値定符号行列である」
　とは、
　Aによって定まる二次形式txAxが半負値定符号二次形式となること
　　　つまり、零ベクトルでない任意の実n次元数ベクトルxに対して、txAx ≦０となること
　である。

※

　→半負値定符号二次形式

 　
　 　


→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

 　




定義：不定符号二次形式


行列を
用いない
定義


「『x1, x2, x3, …, xnについての二次形式』Q (x1, x2, x3, …, xn)は不定符号である」
とは、
　・「Q (x1, x2, x3, …, xn)＞０」を満たす「x1, x2, x3, …, xn　の値」　
も、
　・「Q (x1, x2, x3, …, xn)＜０」を満たす「x1, x2, x3, …, xn　の値」
も存在することをいう。

したがって、
　Q (x1, x2, x3, …, xn)が不定符号であるならば、　　
　　x1=x2=…=xn=０ではない限りで任意の(x1, x2, …, xn)に対して、
　　　Q (x1, x2, x3, …, xn)の符号を
　　一義的に定められない。
　　

※具体例→2変数の不定符号二次形式　

[文献－解析]
・松坂『解析入門3』14.3-A (p.169):行列を使わずに。


行列を
用いた
定義


「二次形式txAxは不定符号である」
とは、
　　　txAx＞０を満たす実n次元数ベクトルxも存在すれば、
　　　txAx＞０を満たす実n次元数ベクトルxも存在する
ということ。

したがって、
txAxが不定符号だと、
零ベクトルでない任意のxに対して、
　　 txAx の符号
を一義的に定められない。


　 　


→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

 　


　

定義：主小行列 prinaipal submatrix


移動→主小行列

 　

　

定義：主小行列式prinaipal minor , prinaipal subdeterminant

　

移動→主小行列式

 　
　 　

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

　

（reference）

斎藤正彦『基礎数学1：線形代数入門』東京大学出版会、1966年、pp.153-158。
Chiang, Fundamental Methods of Mathematiaal Eaonomias: Third Edition, MaGraw Hill,1984,pp.319-331.極値問題で利用。
岩田暁一『経済分析のための統計的方法(第2版)』東洋経済新報社、1983年、pp.310-322。
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、pp.142-150。
藤原毅夫『理工系の基礎数学2:線形代数』岩波書店、1996年、pp.152-157。
石村園子『すぐわかる線形代数』東京図書、1994年、pp.219-225。
縄田和満『EXAELによる線形代数入門』年、朝倉書店。
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.203-205。
William H. Greene Econometric Analysis (3rd Edition) , Prentiae Hall International, 1997,pp.46-47...