※応用：2変数関数の極値問題
※一般化：n変数の二次形式
※関連：主小行列/主小行列式/固有値　
→線形代数目次/総目次　

定義

・「2変数x,yについての二次形式」とは、
　 2変数x,yについての多項式で、2次の項ばかりからなるもの　
　　すなわち、｢斉２次式｣｢２次同次多項式｣「x,yの2次同次関数」
　　Q (x,y) = ax²+2 bxy + c y²　　　(a,b,cは定数)
　のことをいう。

[文献]
＊松坂『解析入門3』14.3-D (p.172)
・黒田『21世紀の数学1:微分積分学』定理8.15(p.309)
・高橋『微分と積分2』§3.1定理3.6 (p.67)

※性質：二次形式で定義された関数はRⁿ上連続
※応用：2変数関数の極値の十分条件　

行列
表現

「変数x,yについての二次形式」Q(x,y)は
　　h＝
　　A=　
　をつかって、
　行列積 ^thAh　として表せる。
　実際、^thAh　
　　　　＝ (x,y)
　　　　　

　　　　　＝(ax+by , bx+cy)

　　　　　＝(ax+by )x+(bx+cy )y
　　　　　＝ax²+ by x+ bxy+ cy²　
　　　　　＝ax²+ 2bxy+ cy²　　
　　　　　　　
※「二次形式^thAhの(係数)行列」といえば、対称行列Aのことを指す。
※「二次形式^thAhの階数」といえば、対称行列Aの階数のことを指す。
※^thAh　を、対称行列Aによって定まる二次形式という意味で、A[h]とも書く。

※2次形式は、h＝(x, y)の関数であって、R²上で連続（∵）。

例

たとえば、二次形式3x₁²+ 7x₁x₂ + 5 x₂²　なら、　　　　　
　3x₁²+ 7x₁x₂ + 5 x₂²＝3x₁²+ 2・7/2 x₁x₂ + 5 x₂²　（つまり、a₁₂＝7/2　として、）　
　　　＝3x₁²+7/2 x₁x₂ +7/2 x₂x₁ +5 x₂²　
　　　＝ (3x₁ + 7/2 x₂) x₁ +(7/2 x₁+ 5 x₂) x₂　
　　　　
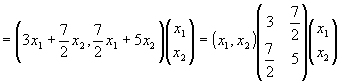
　　と表せる。　

※

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

行列を
用いない
定義

「『x,yについての二次形式』Q (x,y)は正値である」
「『x,yについての二次形式』Q (x,y)は正値定符号二次形式である」
「『x,yについての二次形式』Q (x,y)は正定形式positive formである」
とは、
　x=y=０ではない限りで任意の(x,y)に対して、
　　『x,yについての二次形式』Q (x,y)>０　
　が成り立つこと

つまり、
　原点(０,０)を除く平面R²上のどこでも、
　　　Q (x,y)>０
　が成り立つこと
をいう。

　→　正値定符号行列　　

※一般化→n変数の正値定符号二次形式
※正値定符号になるための条件：
　・2変数二次形式の符号判定〜行列を使わずに
　・正値定の必要十分条件-固有値　
　・正値定の必要十分条件-主小行列式　
※活用例：2変数関数の狭義極小の2階十分条件　


[文献−線型代数]
・佐武『線型代数学』�W§4 (p.161)
・斎藤『線形代数入門』155;
・永田『理系のための線形代数の基礎』149;
・木村『線形代数：数理科学の基礎』2.1(p.36):平方完成との関連。

[文献−解析]
＊杉浦『解析入門１』�U§8定義1(p.153)
＊松坂『解析入門3』14.3-A (p.169):行列を使わずに。
＊松坂『解析入門4』18.2-E (p.107):行列を用いて。

[文献−数理経済]
・入谷久我『数理経済学入門』定義8.2 (p.188).
・Chiang, Fundamental Methods of Mathematiaal Economics, 320.
・岩田『経済分析のための統計的方法』311

行列を
用いた
定義

「二次形式^thAhは正値である」
「二次形式^thAhは正値定符号二次形式である」
「二次形式^thAhは正定形式positive formである」
とは、
　零ベクトルでない任意の実2次元縦ベクトルhに対して
　　　　　二次形式 ^thAh >０　
　が成り立つことをいう。

　→　正値定符号行列　　

※

簡単なかたちの２次形式ならば、
平方完成によって、正値定符号の判定が可能。
複雑な場合は、どのようにして、正値定符号の判定を行うか？
→固有値による正値定符号の判定
→主小行列式による正値定符号の判定

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

1.

正値定符号行列・正定行列とは、
Q (x,y) = = ax²+2 bxy + c y²　が正値定符号二次形式であるとき、
Q (x,y)＝ax²+ 2bxy+ cy² を
　　(x,y)
という形に表した際の
対称行列のことをいう。

2.

要するに、
「行列は正値定符号行列である」
「行列は正定行列である」
　とは、
　によって定まる二次形式(x,y)が正値定符号二次形式となること
　つまり、零ベクトルでない任意の実2次元数ベクトルに対して
　　　　　(x,y) >０
　が満たされること
　である。　

　→正値定符号二次形式

※

簡単なかたちの２次形式ならば、
平方完成によって、正値定符号の判定が可能。
複雑な場合は、どのようにして、正値定符号の判定を行うか？
→固有値による正値定符号の判定
→主小行列式による正値定符号の判定

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

行列を
用いない
定義

「『x,yについての二次形式』Q (x,y)は半正値である」
「『x,yについての二次形式』Q (x,y)は半正値定符号二次形式である」
とは、
　x=y=０ではない限りで任意の(x,y)に対して、
　　『x,yについての二次形式』Q (x,y)≧０　
　が成り立つこと
つまり、
　原点(０,０)を除く平面R²上のどこでも、
　　　Q (x,y)≧０
　が成り立つこと
をいう。

　→　半正値定符号行列　　

※一般化→n変数の半正値定符号二次形式

[文献−線型代数]
・佐武『線型代数学』�W§4 (p.161)
・斎藤『線形代数入門』155;
・永田『理系のための線形代数の基礎』149;

[文献−解析]
＊杉浦『解析入門１』�U§8定義1(p.153)
＊松坂『解析入門3』14.3-A (p.169):行列を使わずに。
＊松坂『解析入門4』18.2-E (p.107):行列を用いて。

[文献−数理経済]
・入谷久我『数理経済学入門』定義8.2 (p.188).
・Chiang, Fundamental Methods of Mathematiaal Economics, 320.
・岩田『経済分析のための統計的方法』311

行列を
用いた
定義

「二次形式^thAhは半正値である」
「二次形式^thAhは半正値定符号二次形式である」
とは、
　零ベクトルでない任意の実2次元縦ベクトルhに対して　
　　　二次形式 ^thAh ≧０　
　が成り立つことをいう。

　→　半正値定符号行列　　

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

1.

半正値定符号行列・半正定行列・非負値符号行列・非負定行列とは、
Q (x,y) = ax²+2 bxy + c y²　が半正値定符号二次形式であるとき、
Q (x,y) = ax²+2 bxy + c y²　を、
　　(x,y)
という形に表した際の
対称行列のことをいう。　　

※一般化→n×nの半正値定符号行列

[文献−線型代数]
・佐武『線型代数学』�W§4 (p.161)
・斎藤『線形代数入門』155;
・永田『理系のための線形代数の基礎』149;
・木村『線形代数：数理科学の基礎』2.3(p.39)。「半正定」「非負定」

[文献−解析]
＊杉浦『解析入門１』�U§8定義1(p.153)
＊松坂『解析入門3』14.3-A (p.169):行列を使わずに。
＊松坂『解析入門4』18.2-E (p.107):行列を用いて。

[文献−数理経済]
・岡田『経済学・経営学のための数学』2.7 (p.113)
・岩田『経済分析のための統計的方法』311
・Greene , Econometric Analysis,46.

2.

要するに、
「行列は半正値定符号行列である」
「行列は半正定行列である」
「行列は非負値符号行列である」
「行列は非負定行列である」
とは、
によって定まる二次形式(x,y)が半正値定符号二次形式となること
　　つまり、
　　零ベクトルでない任意の実2次元数ベクトルに対して、
　　　　　　(x,y) ≧０
　　が満たされること
である。　
　→　半正値定符号二次形式

※

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

行列を
用いない
定義

「『x,yについての二次形式』Q (x,y)は負値である」
「『x,yについての二次形式』Q (x,y)は負値定符号二次形式である」
とは、
　x=y=０ではない限りで任意の(x,y)に対して、
　　『x,yについての二次形式』Q (x,y)<０　
　が成り立つこと
つまり、
　原点(０,０)を除く平面R²上のどこでも、
　　　Q (x,y)<０
　が成り立つこと
をいう。

　→負値定符号行列　　　

※一般化→n変数の負値定符号二次形式
※負値定符号になるための条件：
　・2変数二次形式の符号判定〜行列を使わずに
　・負値定の必要十分条件-固有値　
　・負値定の必要十分条件-主小行列式　
※活用例：2変数関数の狭義極大の2階十分条件　

[文献−線型代数]
・佐武『線型代数学』�W§4 (p.161)
・斎藤『線形代数入門』155;
・永田『理系のための線形代数の基礎』149;

[文献−解析]
＊杉浦『解析入門１』�U§8定義1(p.153)
＊松坂『解析入門3』14.3-A (p.169):行列を使わずに。
＊『解析入門4』18.2-E (p.107):行列を用いて。

[文献−数理経済]
・入谷久我『数理経済学入門』定義8.2 (p.188).
・Chiang, Fundamental Methods of Mathematiaal Economics, 320.
・岩田『経済分析のための統計的方法』311

行列を
用いた
定義

「二次形式^thAhは負値である」
「二次形式^thAhは負値定符号二次形式である」
とは、
　零ベクトルでない任意の実2次元数ベクトルhに対して　
　二次形式 ^thAh ＜０　が成り立つことをいう。

　→　負値定符号行列　　

※

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

1.

負値定符号行列・負定行列とは、
Q (x,y) = = ax²+2 bxy + c y²　が負値定符号二次形式であるとき、
Q(x,y) = = ax²+2 bxy + c y²　を
　　(x,y)
という形に表した際の
対称行列のことをいう。

※一般化→n×nの負値定符号行列
※負値定符号になるための条件：
　・2変数二次形式の符号判定〜行列を使わずに
　・負値定の必要十分条件-固有値　
　・負値定の必要十分条件-主小行列式　
※活用例：2変数関数の狭義極大の2階十分条件　

[文献−線型代数]
・佐武『線型代数学』�W§4 (p.161)
・斎藤『線形代数入門』155;
・永田『理系のための線形代数の基礎』149;

[文献−解析]
＊杉浦『解析入門１』�U§8定義1(p.153)
＊松坂『解析入門3』14.3-A (p.169):行列を使わずに。
＊松坂『解析入門4』18.2-E (p.107):行列を用いて。

[文献−数理経済]
・岡田『経済学・経営学のための数学』2.7 (p.113)
・岩田『経済分析のための統計的方法』311
・Greene , Econometric Analysis,46.

3.

要するに、
「行列は負値定符号行列である」
「行列は負定行列である」
　とは、
　によって定まる二次形式(x,y)が負値定符号二次形式となること
　　　つまり、零ベクトルでない任意の実2次元数ベクトル)に対して、
　　　　　(x,y) ＜０
　　　が満たされること
　である。　

　→　負値定符号二次形式

※

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

行列を
用いない
定義

「『x,yについての二次形式』Q (x,y)は半負値である」
「『x,yについての二次形式』Q (x,y)は半負値定符号二次形式である」
とは、
　x=y=０ではない限りで任意の(x,y)に対して、
　　『x,yについての二次形式』Q (x,y) ≦０　
　が成り立つこと
つまり、
　原点(０,０)を除く平面R²上のどこでも、
　　　Q (x,y)≦０
　が成り立つこと
をいう。

　→　半負値定符号行列　　

※一般化→n変数の半負値定符号二次形式

[文献−線型代数]
・佐武『線型代数学』�W§4 (p.161)
・斎藤『線形代数入門』155;
・永田『理系のための線形代数の基礎』149;

[文献−解析]
＊杉浦『解析入門１』�U§8定義1(p.153)
＊松坂『解析入門3』14.3-A (p.169):行列を使わずに。
＊松坂『解析入門4』18.2-E (p.107):行列を用いて。

[文献−数理経済]
・入谷久我『数理経済学入門』定義8.2 (p.188).
・Chiang, Fundamental Methods of Mathematiaal Economics, 320.
・岩田『経済分析のための統計的方法』311

行列を
用いた
定義

「二次形式^thAhは半負値である」
「二次形式^thAhは半負値定符号二次形式である」
とは、
　零ベクトルでない任意の実2次元数ベクトルhに対して　
　　　　　　二次形式 ^thAh ≦０　
　が成り立つことをいう。

　→　半負値定符号行列　　　

※

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

1.

半負値定符号行列・非正値定符号行列とは、
Q (x,y) =  ax²+2 bxy + c y²　が半負値定符号二次形式であるとき、
Q (x,y)＝ax²+ 2bxy+ cy² を
　　(x,y)
という形に表した際の
対称行列のことをいう。
　

※一般化→n×nの半負値定符号行列

[文献−線型代数]
・佐武『線型代数学』�W§4 (p.161)
・斎藤『線形代数入門』155;
・永田『理系のための線形代数の基礎』149;

[文献−解析]
＊杉浦『解析入門１』�U§8定義1(p.153)
＊松坂『解析入門3』14.3-A (p.169):行列を使わずに。
＊松坂『解析入門4』18.2-E (p.107):行列を用いて。

[文献−数理経済]
・岡田『経済学・経営学のための数学』2.7 (p.113)
・岩田『経済分析のための統計的方法』311
・Greene , Econometric Analysis,46.

2.

要するに、
「行列は半負値定符号行列である」
「行列は非正値定符号行列である」
　とは、
　によって定まる二次形式(x,y)が半負値定符号二次形式となること
　　　つまり、
　　　零ベクトルでない任意の実2次元数ベクトルに対して、
　　　　　　　(x,y) ≦０
　　　が満たされること
　である。

※

　→半負値定符号二次形式

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

行列を
用いない
定義

「『x,yについての二次形式』Q (x,y)は不定符号である」
とは、
　　「Q (x,y)＞０かつ『x=y=０でない』」を満たす(x,y)も、
　　「Q (x,y)＜０かつ『x=y=０でない』」を満たす(x,y)も、
　　　存在する
ということ、
つまり、
　　　原点(０,０)を除く平面R²上に、
　　　　　Q (x,y)＞０を満たす点も、　
　　　　　Q (x,y)＜０を満たす点も
　　　存在する
ということ。

したがって、
Q (x,y)が不定符号だと、
　x=y=０ではない限りで任意の(x, y)に対して、
　　Q (x,y)の符号を
一義的に定めらることはできなくなる。

※一般化→n変数の不定符号二次形式

[文献−解析]
・松坂『解析入門3』14.3-A (p.169):行列を使わずに。

行列を
用いた
定義

「二次形式^thAhは不定符号である」
とは、
　　「^thAh＞０かつh≠〇」を満たす実2次元縦ベクトルhの値も、
　　「^thAh＜０かつh≠〇」を満たす実2次元縦ベクトルhの値も存在する
ということ。

したがって、
^thAhが不定符号であると、
零ベクトルでない任意の実2次元縦ベクトルhに対して、　
　　　^thAhの符号を、
一義的に定めることはできない。

→[トピック一覧：二次形式]
→[線形代数目次/総目次]　

半定符号二次形式とは、
半正値定符号二次形式・半負値定符号二次形式の総称。

つまり、
「『x,yについての二次形式』Q (x,y)は半定符号である」
とは、
　　　Q (x,y)が半正値定符号二次形式である
　　　または、
　　　Q (x,y)が半負値定符号二次形式である
ということを指す。

[文献−解析]
・松坂『解析入門3』14.3-C (p.169):行列を使わずに。