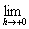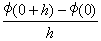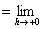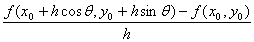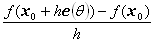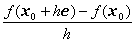2変数関数の方向微分可能・方向微分係数・導関数の定義：トピック一覧　　

　・1点における方向微分可能性・微分係数の定義：方向微分可能・方向微分係数[原意/操作化/定義1/定義2]　
　・1点における方向微分係数の計算公式−偏微分係数から計算可　　
　・　　

※2変数関数の微分関連ページ： 偏微分/ 高次の偏微分/ 微分演算子/ 全微分/ 2階全微分/ 高階全微分　
※2変数関数微分の応用：合成関数の微分/平均値定理･テイラーの定理/極値問題/陰関数定理/逆関数定理/ラグランジュ未定乗数法
※2変数関数に関する他の概念：2変数関数の諸属性/極限/連続/極限の性質/偏微分/全微分/矩形上の積分/点集合上の積分　
※微分関連ページ：1変数関数の微分 / n変数関数の偏微分/ n変数関数の全微分/ n変数ベクトル値関数の偏微分/ n変数ベクトル値関数の全微分　　
→総目次

定義：2変数関数は点(x₀, y₀)で方向微分可能differentiable・点(x₀, y₀)における方向微分係数differential coefficient　

原意

[文献−数学]
・高橋『微分と積分2』§3.2 (pp.73-4): 2変数関数；
・笠原『微分積分学』5.1例3(p.157): 2変数関数
・小形『多変数の微分積分』pp. 51-53:2変数関数。
・杉浦『解析入門』�U§3定義1 (p.107)：n変数m値ベクトル値関数；
・黒田『微分積分学』8.3.3定義8.10(pp.287) ：n変数実数値関数；.
・Lang,Undergraduate Analysis,15-§2-application(p.325): n変数実数値関数directional derivative;
・清野「多変数関数の微分」第3回/第4回
[文献−数理経済学]
・高橋一『経済学とファイナンスのための数学』5.2�V方向微分(p.149) ：n変数実関数.
・de la Fuente, Mathematical Methods and Models for Economists, PartI-4-2-Definition2.1 (pp.163-4) ：n変数実数値関数.

[一般化]
・多変数関数の方向微分
・ベクトル値関数の方向微分

操作化

[原意の操作化]
2変数関数f (x,y )の点(x₀, y₀)におけるθ方向微分係数は、以下の手順で、操作化される。
1. xy 平面上で、
　点(x₀, y₀)から、x軸プラス方向からθ度だけ逆時計回りさせた方向に、
　新たな座標軸tを設定[上図の水色の直線]。
　なお、t≧０のみを考え、t<０は考えないことにする。
　t座標の０は、(x, y)座標の(x₀, y₀)を表し、
　t座標の1は、(x, y)座標の(x₀+cosθ, y₀+ sinθ)を表し、
　一般に、t座標のt (>０)は、(x, y)座標の(x₀+ t cosθ, y₀+t sinθ)を表す。
2. t-z平面で、f (x,y )のグラフを切断する。
3.切断面に現れる曲線のグラフは、当然、t-z平面上にあるので、。
　この曲線を、1変数関数z=φ(t)＝f ( x₀+ t cosθ, y₀+ t sinθ)と表せる。　
4.「f (x,y )の点(x₀, y₀)におけるθ方向微分係数」とは、
　　「切断面[t-z平面]のなかで、曲線z=φ(t)に、t=0で接する接線の傾き」であって、　
　　「t =０におけるz=φ(t)の右微分係数」として表せる。　　

5.　「t =０におけるz=φ(t)の右微分係数」は、
　　二様に操作化されることから、
　　「f (x,y )の点(x₀, y₀)におけるθ方向微分係数」も
　　二様に操作化される。
　　　
　　[操作化１]　→　定義1 　　
　　「t =０におけるz=φ(t)の右微分係数」を、
　　　　
　　というかたちに操作化した場合、
　　1変数関数z=φ(t)＝f ( x₀+ t cosθ, y₀+ t sinθ) だから、
　　「t =０におけるz=φ(t)の右微分係数」は、
　　　　　
　　となるので、
　　「f (x,y )の点(x₀, y₀)におけるθ方向微分係数」は、　　
　　　　
　と表せることがわかる。

　　[操作化2]　→　定義2　　　
　　「t =０におけるz=φ(t)の右微分係数はA」を、
　　「点t =０に対して、ある一定の実数Aが存在して、　
　　　　　　φ( t )−（φ(０) +A(t−０) ）＝o ( t−０)　　(t→０ +０)　
　　　　　　すなわち、
　　　　　　φ( t )−（φ(０) +At ）＝o (t)　　(t→ +０)　
　　　を満たす」
　　　というかたちに操作化した場合、　
　　　1変数関数z=φ(t)＝f ( x₀+ t cosθ, y₀+ t sinθ) だから、
　　　「f (x,y )の点(x₀, y₀)におけるθ方向微分係数」は、　　
　　　　　　f ( x₀+ t cosθ, y₀+ t sinθ)−（f ( x₀, y₀ )+At ）＝o (t)　　(t→ +０)　
　　　と表せることがわかる。

定義1

[角度θで方向を指定する場合の方向微分の定義−ベクトルを使わない表現]

・「f (x,y )は点(x₀, y₀)において角度θ方向に微分可能である」
　とは、
　1変数関数φ(t)=f (x₀+t cosθ, y₀+t sinθ)　について、
　t =０における右微分係数　
　　　すなわち、
　　　有限な右極限値
　　　　
　　　　　
　が存在することをいう。

・f (x,y )が点(x₀, y₀)において角度θ方向に微分可能であるとき、
　「f (x,y )の点(x₀, y₀)におけるθ方向微分係数」　
　とは、
　1変数関数φ(h)=f (x₀+h cosθ, y₀+h sinθ)　についての、
　h =０における右微分係数　
　　　すなわち、
　　　有限な右極限値
　　　　
　　　　　
　のことをいう。

[文献−数学]
・笠原『微分積分学』5.1例3(p.157): 2変数関数
・小形『多変数の微分積分』pp. 51-53:2変数関数。

[角度θで方向を指定する場合の方向微分の定義−ベクトル表現]

・「z=f (x)は実2次元数ベクトルx ₀において角度θ方向に微分可能」とは、
　実2次元数ベクトル e(θ)=( cosθ, sinθ)　にたいして、
　有限な右極限値
　　　　
　が存在することをいう。
　　*　hは実数、　
　　　 he(θ)は、実2次元数ベクトルe(θ)のスカラー倍、
　　　 x₀+he　は、x₀とh eとのベクトル和を表す。　

・z=f (x)が実2次元数ベクトルx ₀において角度θ方向に微分可能であるとき、
　「x₀におけるz=f (x)のe方向微分係数」とは、
　e(θ)=( cosθ, sinθ)　にたいする有限な右極限値
　　　　
　のことを指す。
　　*　hは実数、　
　　　 he(θ)は、実2次元数ベクトルe(θ)のスカラー倍、
　　　 x₀+he　は、x₀とh eとのベクトル和を表す。　
　　　
・「x₀におけるz=f (x)のe方向微分係数」を、
　e=( cosθ, sinθ)　を用いて、
　　　D_e(θ) f (x₀)
　と表す。　

[文献−数学]
・黒田『微分積分学』8.3.3定義8.10(pp.287) ：n変数実数値関数；.

[単位ベクトルで方向を指定する場合の方向微分の定義]
角度θの代わりに、単位ベクトルを用いて方向を指定して、
方向微分を定義することもできる。
・「z=f (x)は実2次元数ベクトルx ₀においてe方向に微分可能」とは、
　実2次元単位ベクトル e=( e₁ , e₂)　にたいして、
　有限な右極限値
　　　　
　が存在することをいう。
　　*　hは実数、　
　　　 heは、実2次元単位ベクトルeのスカラー倍、
　　　 x₀+ h e　は、x₀とh eとのベクトル和を表す。
　　*　e=( e₁ , e₂ ) 方向とは、
　　　　　x-y平面上の直線{(x, y ) | x=x₀+t e₁ かつ y=y₀+t e₂ かつ t≧０}　
　　　の方向を表す。

・z=f (x)が実2次元数ベクトルx ₀においてe方向に微分可能であるとき、
　「x₀におけるz=f (x)のe方向微分係数」とは、
　実2次元単位ベクトル e=( e₁ , e₂ )にたいする有限な右極限値
　　　
　のことを指す。
　　*　hは実数、　
　　　 heは、実2次元単位ベクトルeのスカラー倍、
　　　 x₀+ h e　は、x₀とh eとのベクトル和を表す。　
　　*　e=( e₁ , e₂ ) 方向とは、
　　　　　x-y平面上の直線{(x, y ) | x=x₀+t e₁ かつ y=y₀+t e₂ かつ t≧０}　
　　　の方向を表す。

・「x₀におけるz=f (x)のe方向微分係数」を、
　　　D_e f (x₀)
　と表す。　

[文献−数学]
・黒田『微分積分学』8.3.3定義8.10(pp.287) ：n変数実数値関数；.
・高橋『微分と積分2』定理3.14 (p.74): 2変数関数；

定義2

・「f (x,y )は点(x₀, y₀)でθ方向微分可能であって、
　　f (x,y )の点(x₀, y₀)におけるθ方向微分係数はA」
とは、
　f ( x₀+ t cosθ, y₀+ t sinθ)−（f ( x₀, y₀ )+At ）＝o (t)　　(t→ +０)　
が満たされることをいう。

・「z=f (x)は実2次元数ベクトルx ₀においてe方向に微分可能であって、
　　x₀におけるz=f (x)のe方向微分係数はA」
　とは、
　実2次元単位ベクトル e=( e₁ , e₂)　にたいして、
　　f ( x₀+ te )−（f ( x₀ )+At ）＝o (t)　　(t→ +０)　
　が満たされることをいう。
　　* teは、実2次元単位ベクトルeのスカラー倍を表し、
　　　x₀+ te　は、x₀とteとのベクトル和を表す。　
・「x₀におけるz=f (x)のe方向微分係数」を、
　　　D_e f (x₀)
　と表す。　

[文献]

定理：方向微分係数の計算公式 − 偏微分係数から計算可能

[角度θで方向を指定された方向微分係数の場合−ベクトルを使わない表現]

2変数関数f (x,y )が点(x₀, y₀)において全微分可能ならば、
2変数関数f (x,y )は、点(x₀, y₀)で、任意の角度θ方向に方向微分可能で、
「f (x,y )の点(x₀, y₀)におけるθ方向微分係数」は、　
　　f _x ( x₀, y₀ ) cosθ+ f _y (x₀, y₀ ) sinθ
となる。

[文献−数学]
・高橋『微分と積分2』定理3.14 (p.74): 2変数関数；
・笠原『微分積分学』5.1例3(p.157): 2変数関数
・小形『多変数の微分積分』pp. 52:2変数関数。
・黒田『微分積分学』8.3.3定理8.11(pp.288) ：n変数実数値関数；.
・志賀『解析入門30講』25講(p.195) :２変数関数;
・『岩波数学辞典』333G全微分(p.985)：２変数実関数.

[角度θで方向を指定された方向微分係数の場合−ベクトルを使う表現]

2変数関数f (x,y )が点(x₀, y₀)において全微分可能ならば、
2変数関数f (x,y )は、点(x₀, y₀)で、任意の角度θ方向に方向微分可能で、
「f (x,y )の点(x₀, y₀)におけるθ方向微分係数」は、
　　grad f (x₀,y₀)＝（f _x ( x₀, y₀ ), f _y (x₀, y₀ ) ）と e(θ)=( cosθ, sinθ)　との内積　
　　　　　grad f (x₀,y₀) ・ e(θ)　　
　　となる。
つまり、D_e(θ) f (x₀,y₀)＝grad f (x₀,y₀) ・e(θ)

[文献−数学]
・小形『多変数の微分積分』pp. 53:2変数関数。
・杉浦『解析入門』�U§5定理5.2 (p.121)：n変数実数値関数；
・黒田『微分積分学』8.3.3式8.54(pp.289) ：n変数実数値関数；

[一般化]
・多変数関数の方向微分
・ベクトル値関数の方向微分

[単位ベクトルで方向を指定された方向微分係数の場合]

2変数関数f (x,y )が点(x₀, y₀)において全微分可能ならば、
2変数関数f (x,y )は、点(x₀, y₀)で、任意のe方向に方向微分可能で、
「f (x,y )の点(x₀, y₀)におけるe方向微分係数」は、
　　grad f (x₀,y₀)＝（f _x ( x₀, y₀ ), f _y (x₀, y₀ ) ）と e　との内積　
　　　　　grad f (x₀,y₀) ・ e　　
　　となる。
つまり、D_e(θ) f (x₀,y₀)＝grad f (x₀,y₀) ・e