数ベクトル空間の次元 : トピック一覧:次元
・定理:一次結合が一次従属であることと、一次結合の個数・一次結合を構成するベクトルの個数との、関連性 1/2
・定理:数ベクトルの個数と、一次独立・従属の関係
・定理:数ベクトルが基底となる十分条件,数ベクトルが基底とならない十分条件/一次独立なベクトルからの基底の生成
・定理:数ベクトル空間の次元
※数ベクトル空間関連ページ:数ベクトル空間の定義/線形結合/一次独立・一次従属/基底
※一般のベクトル空間における次元の定義/実n次元数ベクトル空間の次元
定理:一次結合が一次従属となるための十分条件(1):一次結合の個数・一次結合を構成するベクトルの個数と、一次従属
【舞台設定】
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
Kn:体K上のn次元数ベクトル空間
+:体K上のn次元数ベクトル空間Knにおいて定義されているベクトルの加法
スカラーに続けてベクトルを並べて書いたもの:K上のn次元数ベクトル空間Knにおいて定義されているスカラー乗法
v1, v2, …, vl:l個の「Kからつくったn次元数ベクトル」。
具体的に書くと、i=1,2,…, lにたいして、vi1, vi2, …, vin∈Kとして、vi=( vi1, vi2, …, vin )
したがって、v1, v2, …, vl ∈Kn。
なお、個数lが有限個であることに注意。
a1, a2, …, al :スカラー。a1, a2, …, al ∈K
【本題】
「Kからつくったn次元数ベクトル」v1, v2, …, vl の一次結合を(l+1)個つくる。
これら(l+1)個の「v1, v2, …, vlの一次結合」は一次従属。
つまり、
w1=a11v1+a12v2+…+a1lvl (a11, a12, …, a1l ∈K、v1, v2, …, vl ∈Kn )
w2=a21v1+a22v2+…+a2lvl (a21, a22, …, a2l ∈K、v1, v2, …, vl ∈Kn )
:
wl=al1v1+al2v2+…+allvl (al1, al2, …, all ∈K、v1, v2, …, vl ∈Kn )
w(l+1)=a(l+1)1 v1+a(l+1)2v2+…+a(l+1)lvl (a(l+1)1, a(l+1)2, …, a(l+1)l ∈K、v1, v2, …, vl ∈Kn )
は一次従属。
※「v1, v2, …, vlの一次結合」も「Kからつくったn次元数ベクトル」であることに注意。
※なぜ?→証明
【文献】
永田『理系のための線形代数の基礎』補題1.2.1(p.12)
定理:一次結合が一次従属となるための十分条件(2)一次結合の個数・一次結合を構成するベクトルの個数と、一次従属
【舞台設定】
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
Kn:体K上のn次元数ベクトル空間
+:体K上のn次元数ベクトル空間Knにおいて定義されているベクトルの加法
スカラーに続けてベクトルを並べて書いたもの:K上のn次元数ベクトル空間Knにおいて定義されているスカラー乗法
v1, v2, …, vl:l個の「Kからつくったn次元数ベクトル」。
具体的に書くと、i=1,2,…, lにたいして、vi1, vi2, …, vin∈Kとして、vi=( vi1, vi2, …, vin )
したがって、v1, v2, …, vl ∈Kn。
なお、個数lが有限個であることに注意。
a1, a2, …, al :スカラー。a1, a2, …, al ∈K
【本題】
命題:「Kからつくったn次元数ベクトル」v1, v2, …, vl の一次結合をm個つくる。
m>l ならば、m個の「v1, v2, …, vlの一次結合」は一次従属。
つまり、
w1=a11v1+a12v2+…+a1lvl (a11, a12, …, a1l ∈K、v1, v2, …, vl ∈Kn )
w2=a21v1+a22v2+…+a2lvl (a21, a22, …, a2l ∈K、v1, v2, …, vl ∈Kn )
:
wm=am1v1+am2v2+…+amlvl (am1, am2, …, aml ∈K、v1, v2, …, vl ∈Kn )
であって、
m>l ならば、w1, w2, …, wmは一次従属。
上記命題の対偶:
「Kからつくったn次元数ベクトル」v1, v2, …, vlの一次結合をm個つくる。
m個の「v1, v2, …, vlの一次結合」が一次独立ならば、m≦l。
つまり、
w1=a11v1+a12v2+…+a1lvl (a11, a12, …, a1l ∈K、v1, v2, …, vl ∈Kn )
w2=a21v1+a22v2+…+a2lvl (a21, a22, …, a2l ∈K、v1, v2, …, vl ∈Kn )
:
wm=am1v1+am2v2+…+amlvl (am1, am2, …, aml ∈K、v1, v2, …, vl ∈Kn )
であって、
w1, w2, …, wmが一次独立ならば、m≦l。
(証明)
・w1, w2, …, wl, w(l+1)は一次従属。(∵)
・w1, w2, …, wl, w(l+1)が一次従属であって、m>l ならば、
w1, w2, …, wl, w(l+1),w(l+2), …, wmは一次従属。 (∵)
【文献】
永田『理系のための線形代数の基礎』補題1.2.1(p.12)
定理:数ベクトルの個数と、一次独立・従属の関係
【舞台設定】
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
Kn:体K上のn次元数ベクトル空間
+:体K上のn次元数ベクトル空間Knにおいて定義されているベクトルの加法
スカラーに続けてベクトルを並べて書いたもの:K上のn次元数ベクトル空間Knにおいて定義されているスカラー乗法
v1, v2, …, vm:m個の「Kからつくったn次元数ベクトル」。
具体的に書くと、i=1,2,…, mにたいして、vi1, vi2, …, vin∈Kとして、vi=( vi1, vi2, …, vin )
したがって、v1, v2, …, vm ∈Kn。
なお、個数mが有限個であることに注意。
a1, a2, …, al :スカラー。a1, a2, …, al ∈K
【本題】
命題:「Kからつくったn次元数ベクトル」v1, v2, …, vm が m>n ならば、v1, v2, …, vm は一次従属。
(v1, v2, …, vmが m≦n ならば、v1, v2, …, vmは一次従属の場合もあれば一次独立の場合もある)
上記命題の対偶:「Kからつくったn次元数ベクトル」v1, v2, …, vmが一次独立ならば、v1, v2, …, vmは m≦n。
(vv1, v2, …, vmが一次従属ならば、v1, v2, …, vmはm>nの場合もあればm≦nの場合もある)
【図解】
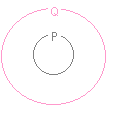
Pの内側:n個より多いn次元数ベクトル
Pの外側:n個以下のn次元数ベクトル
Qの内側:一次従属なn次元数ベクトル
Qの外側:一次独立なn次元数ベクトル
【証明】
・「Kからつくったn次元数ベクトル」はどれでも、
Knにおける単位ベクトルe1, e2, …, enの一次結合として表せる。(∵)
したがって、v1, v2, …, vmも、それぞれ、e1, e2, …, enの一次結合として表せる。…(1)
・Knにおける単位ベクトルe1, e2, …, enの一次結合を、n個よりも多くつくると、
それらのの一次結合どおしは、一次従属。(∵) …(2)
・(1)(2)より、「Kからつくったn次元数ベクトル」v1, v2, …, vmは、m>n ならば、一次従属。
【文献】
永田『理系のための線形代数の基礎』定理1.2.2(p.13)
定理:数ベクトルが基底となるための十分条件
【舞台設定】
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
Kn:体K上のn次元数ベクトル空間
+:体K上のn次元数ベクトル空間Knにおいて定義されているベクトルの加法
スカラーに続けてベクトルを並べて書いたもの:K上のn次元数ベクトル空間Knにおいて定義されているスカラー乗法
v1, v2, …, vn:n個の「Kからつくったn次元数ベクトル」。
具体的に書くと、i=1,2,…,nにたいして、vi1, vi2, …, vin∈Kとして、vi=( vi1, vi2, …, vin )
したがって、v1, v2, …, vn ∈Kn。
なお、個数nが有限個であることに注意。
a1, a2, …, an :スカラー。a1, a2, …, an ∈K
【本題】
「Kからつくったn次元数ベクトル」においては、n個の一次独立な「Kからつくったn次元数ベクトル」がそろえば、基底となる。
つまり、v1, v2, …, vn ∈Knが一次独立ならば、v1, v2, …, vnは、Knの基底である。
※ポイントは、「n個」と一次独立。
※なぜ?→証明
【文献】
永田『理系のための線形代数の基礎』系1.2.3(p.13)
定理:数ベクトルが基底とならないことの十分条件
【舞台設定】
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
Kn:体K上のn次元数ベクトル空間
+:体K上のn次元数ベクトル空間Knにおいて定義されているベクトルの加法
スカラーに続けてベクトルを並べて書いたもの:K上のn次元数ベクトル空間Knにおいて定義されているスカラー乗法
v1, v2, …, vn:n個の「Kからつくったn次元数ベクトル」。
具体的に書くと、i=1,2,…,nにたいして、vi1, vi2, …, vin∈Kとして、vi=( vi1, vi2, …, vin )
したがって、v1, v2, …, vn ∈Kn。
なお、個数nが有限個であることに注意。
a1, a2, …, an :スカラー。a1, a2, …, an ∈K
【本題】
「Kからつくったn次元数ベクトル」v1, v2, …, vl の個数lがnより少ないならば、
v1, v2, …, vl が一次従属の場合もあれば一次独立の場合もありえる。
もし、ここで、v1, v2, …, vlが一次独立だとしても
v1, v2, …, vlは、Knの基底になりえない。
※なぜ?→証明
【文献】
永田『理系のための線形代数の基礎』定理1.2.4(p.14)
定理:一次独立なベクトルからの基底の生成
【舞台設定】
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
Kn:体K上のn次元数ベクトル空間
+:体K上のn次元数ベクトル空間Knにおいて定義されているベクトルの加法
スカラーに続けてベクトルを並べて書いたもの:K上のn次元数ベクトル空間Knにおいて定義されているスカラー乗法
v1, v2, …, vn:n個の「Kからつくったn次元数ベクトル」。
具体的に書くと、i=1,2,…,nにたいして、vi1, vi2, …, vin∈Kとして、vi=( vi1, vi2, …, vin )
したがって、v1, v2, …, vn ∈Kn。
なお、個数nが有限個であることに注意。
a1, a2, …, an :スカラー。a1, a2, …, an ∈K
【本題】
K上のn次元数ベクトル空間においては、一次独立な「Kからつくったn次元数ベクトル」に、適当な単位ベクトルを補充することによって基底をつくることができる。
つまり、
v1, v2, …, vn ∈Kn が 一次独立ならば、
ある単位ベクトルei(1), ei(2) ,…, ei(n-l) が存在して、
v1, v2, …, vn, ei(1), ei(2) ,…, ei(n-l)は、Knの基底となる。 。
【補足説明:ベクトルの個数と上記定理の関連】
「Kからつくったn次元数ベクトル」、v1, v2, …, vl の個数lで、場合分けをする。
[case1] l > n
「Kからつくったn次元数ベクトル」v1, v2, …, vl の個数lが、nより多いならば、
v1, v2, …, vlは、つねに一次従属であって、一次独立であることはありえない。(∵)
だから、この場合に、上記定理の仮定「v1, v2, …, vl∈Knが一次独立ならば」が成り立つことはない。
このケースでは、上記定理に出番はない。
[case2] l = n
「Kからつくったn次元数ベクトル」v1, v2, …, vl の個数lがnならば、
v1, v2, …, vl=vnが一次従属の場合もあれば一次独立の場合もありえる。
もし、ここで、上記定理の仮定が成り立ち、v1, v2, …, vl=vnが一次独立ならば、(∵)
v1, v2, …, vl=vnは、すでに、Knの基底である。(∵)
だから、このケースでは、上記定理は自明なのであって、ありがた味がない。
[case3] l < n
「Kからつくったn次元数ベクトル」v1, v2, …, vl の個数lがnより少ないならば、
v1, v2, …, vlが一次従属の場合もあれば一次独立の場合もありえる。
もし、ここで、上記定理の仮定が成り立ち、v1, v2, …, vlが一次独立だとしても
v1, v2, …, vlは、Knの基底になりえない。
一次独立なn次元数ベクトルv1, v2, …, vlが、基底の定義を満たすには、
v1, v2, …, vlの一次結合として、Knに属す「任意の」n次元数ベクトルを表すことができなければならないが、
これは不可能である。
v1, v2, …, vlの一次結合としては表し得ない「Kからつくったn次元数ベクトル」があることは、
次の点について考えてみると判然とする。
|Knの単位ベクトルは、いつでもn個ある。
|また、Knの単位ベクトルは、いつでも一次独立である。(∵)
|つまり、Knには、一次独立なn個のn次元数ベクトルが、単位ベクトルを実例として存在している。
|ところが、
|l < nという設定下で、v1, v2, …, vlの一次結合をn個つくると、
|このn個の「v1, v2, …, vlの一次結合」は一次従属にしかならない。(∵)
|「v1, v2, …, vlの一次結合」としてあらわしうる、一次独立なベクトルの個数は、l以下である。(∵)
|したがって、
|単位ベクトルを実例とする、一次独立なn個のn次元数ベクトルを、「v1, v2, …, vlの一次結合」として表そうとしても、
|表せない(n-l)個のベクトルが存在することになる。
したがって、「Kからつくったn次元数ベクトル」v1, v2, …, vl の個数lがnより少ないケースにおいて、
「一次独立なn次元数ベクトルに、適当な単位ベクトルを補充することによって基底をつくることができる」
とする上記定理は、意義をもつ。
※なぜ?→証明
【文献】
永田『理系のための線形代数の基礎』定理1.2.4(p.14)
定理:数ベクトル空間Knの次元
【舞台設定】
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
Kn:体K上のn次元数ベクトル空間
【本題】
体K上のn次元数ベクトル空間Knの基底は、いつでもn個のn次元数ベクトルからなる。
つまり、
体K上のn次元数ベクトル空間Knの次元は、n。 dim Kn = n
※実n次元数ベクトル空間の次元
【証明】
l個の任意の「Kからつくったn次元数ベクトル」v1, v2, …, vlについて、以下のことが成り立つ。
・l<nのケース(v1, v2, …, vlが一次独立であるケースも一次従属であるケースも含む)
l個の任意の「Kからつくったn次元数ベクトル」v1, v2, …, vlは、Knの基底とならない。
なぜなら、Knの基底であるための条件P2を満たせないから。(∵)
・l>nのケース
l個の任意の「Kからつくったn次元数ベクトル」v1, v2, …, vlは、Knの基底とならない。
なぜなら、l>nならば、定理によって、v1, v2, …, vlは常に一次従属となって、
Knの基底であるための条件P1:一次独立を満たせないから。
・l=nのケース
・l個の任意の「Kからつくったn次元数ベクトル」v1, v2, …, vlが一次独立ならば、
v1, v2, …, vlは、Knの基底となる。(∵)
・l個の任意の「Kからつくったn次元数ベクトル」v1, v2, …, vlが一次従属ならば、
v1, v2, …, vlは、Knの基底とならない。(Knの基底であるための条件P1:一次独立を満たせないから。)
要するに、
(i) l=nかつ「v1, v2, …, vlが一次独立」ならば、
v1, v2, …, vlは、Knの基底となる。
(ii) 「l=nかつ『v1, v2, …, vlが一次独立』」が成り立たないならば、
すなわち、l≠nまたは「l=nかつ『v1, v2, …, vlが一次従属』」ならば、
v1, v2, …, vlは、Knの基底とならない。
(i)(ii)の条件は、あらゆる場合を尽くしており、また(i)(ii)の結論は同時に成り立たないので、
転換法により、
l個の任意の「Kからつくったn次元数ベクトル」v1, v2, …, vlについて、
(i)' v1, v2, …, vlが、Knの基底ならば、
l=nかつ「v1, v2, …, vlが一次独立」
(ii)' v1, v2, …, vlが、Knの基底とならないならば、
l≠nまたは「l=nかつ『v1, v2, …, vlが一次従属』」
といえる。
「v1, v2, …, vlが、Knの基底である」ことの定義には、「v1, v2, …, vlが一次独立」ということが含まれているから、
(i)'は、
(i)'' v1, v2, …, vlが、Knの基底ならば、l=n
といってよい。
以上で、
体K上のn次元数ベクトル空間Knの基底は、どれもn個のn次元数ベクトルからなることが示された。
【文献】
・永田『理系のための線形代数の基礎』1.2(p.13);1.3(p.23)
・神谷浦井『経済学のための数学入門』§3.1.4(p.115)
(reference)
日本数学会編集『岩波数学辞典(第三版)』 岩波書店、1985年、項目210線形空間(pp.570-576)
線形代数のテキスト
志賀浩二『数学30講シリーズ:線形代数30講』朝倉書店、1988年、15講基底と次元(pp.94-99):有限次元ベクトル空間のみ扱っている。
ホフマン・クンツェ『線形代数学I』培風館、1976年、2.3基底と次元(pp.41-50)。
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、1.3ベクトル空間(pp.14-6)。
砂田利一『現代数学への入門:行列と行列式』2003年、§5.3-b(p.173).
佐武一郎『線形代数学(第44版)』裳華房、1987年、Ⅲベクトル空間§6ベクトル空間の公理化(p.115)。線形従属・独立については、数ベクトルに限定?
藤原毅夫『理工系の基礎数学2:線形代数』岩波書店、1996年、4.1線形空間と写像(p.91)。 線形従属・独立については、数ベクトルに限定?
斎藤正彦『線形代数入門』東京大学出版会、1966年、第4章§2線形空間(p.96):実線形空間・複素線形空間のみ;附録Ⅲ§2体(p.249)。
代数学のテキスト
本部均『新しい数学へのアプローチ5:新しい代数』共立出版、1969年、5.2-Aベクトル空間(p.132)。
酒井文雄『共立講座21世紀の数学8:環と体の理論』共立出版、1997年、1.6ベクトル空間(p.22):数ページしか触れていないが、逆に、一般の線形空間の理論の骨組みだけを浮かびあがってくるので、何が重要事項なのかを見極める上で便利。
数理経済学のテキスト
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、§3.1ベクトル空間とは何か(p.105)。
