部分ベクトル空間の次元
: トピック一覧
・定理:ベクトル空間とその部分空間の次元,ベクトル空間の2つの部分空間の次元,
・定理: 和空間の次元、直和と線形独立、直和の次元
※関連ページ:
部分ベクトル空間:定義、部分ベクトル空間の性質、~が張る部分空間、和・直和、直和が定める射影
実ベクトル空間関連ページ:実ベクトル空間の定義、一次結合、線形従属・線形独立、基
底、次元
定理:ベクトル空間とその部分空間の次元
[永田『理系のための線形代数の基礎』定理1.5.1(p.32):証明付;志賀『線形代数30講』21講(p.132);
ホフマン・クンツェ『線形代数学I』2.3基底と次元定理5系1(p.47);
砂田『行列と行列式』§5.3-d定理5.62(p.179).]
【舞台設定】
R:実数体(実数をすべて集めた集合)
V:実ベクトル空間 (実数体R上の線形空間・ベクトル空間」)
W:Vの部分ベクトル空間
【本題】
1. Vの部分ベクトル空間の次元が、Vの次元より大きくなることはない。
つまり、
任意の「実数体R上の有限次元ベクトル空間」について、
Wが「Vの部分ベクトル空間」ならば、
dimW≦dimV
2. 「Vの部分ベクトル空間」で、次元が「Vの次元」に等しいものがあるなら、それは、V自身。
つまり、
任意の「実数体R上の有限次元ベクトル空間」について、
Wが「Vの部分ベクトル空間」、かつ、dimW=dimV ならば、
W=V
定理:ベクトル空間の2つの部分空間の次元
[永田『理系のための線形代数の基礎』系1.5.2(p.32);;斎藤『線形代数入門』4章§4[4.6](p.109);
ホフマン・クンツェ『線形代数学I』2.3基底と次元定理6(p.47)]
【舞台設定】
R:実数体(実数をすべて集めた集合)
V:実ベクトル空間 (実数体R上の有限次元ベクトル空間」)
W1:Vの部分ベクトル空間
W2:Vの部分ベクトル空間
【本題】
任意の「実数体R上の有限次元ベクトル空間」Vの任意の部分ベクトル空間W1,W2について、
W1⊆W2 かつ、dimW1=dimW2 ならば、
W1=W2
定理:和空間の次元
[永田『理系のための線形代数の基礎』定理1.5.3(p.33):証明付;;斎藤『線形代数入門』4章§4[4.7](p.109)]
【舞台設定】
R:実数体(実数をすべて集めた集合)
V:実ベクトル空間 (実数体R上の線形空間・ベクトル空間」)
W1:Vの部分ベクトル空間
W2:Vの部分ベクトル空間
【本題】
任意の「実数体R上の有限次元ベクトル空間」Vの任意の部分ベクトル空間W1,W2について、
dim(W1+W2)=dimW1+dimW2-dim(W1∩W2)
定理:直和と線形独立性
[砂田『行列と行列式』§5.3-a定理5.35(p.171):証明付]
【舞台設定】
R:実数体(実数をすべて集めた集合)
V:実ベクトル空間 (実数体R上の線形空間・ベクトル空間」)
W1,W2,…,Wk:Vの部分ベクトル空間
【本題】
1.
実ベクトル空間Vが、その部分ベクトル空間W1 ,W2 ,…,Wkの直和に分解される
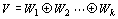
ならば、
W1 に属す任意のベクトルv1
W2 に属す任意のベクトルv2
: :
: :
Wk に属す任意のベクトルvk
のなかで、零ベクトルでないベクトルは、線形独立となる。
2.
V=W1+W2+…+Wn
かつ
W1 に属す任意のベクトルv1
W2 に属す任意のベクトルv2
: :
: :
Wk に属す任意のベクトルvk
のなかで、零ベクトルでないベクトルが線形独立となる
ならば、
実ベクトル空間Vが、その部分ベクトル空間W1 ,W2 ,…,Wkの直和に分解される
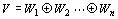
定理:直和の次元
[永田『理系のための線形代数の基礎』系1.5.4(p.34);砂田『行列と行列式』§5.3-d例題5.67(p.181):証明付]
【舞台設定】
R:実数体(実数をすべて集めた集合)
V:実ベクトル空間 (実数体R上の線形空間・ベクトル空間」)
W1,W2,…,Wk:Vの部分ベクトル空間
【本題】
1.
実ベクトル空間Vが、その部分ベクトル空間W1 ,W2の直和に分解される
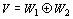
ならば、
dim(V)=dimW1+dimW2
2.
実ベクトル空間Vと、その部分ベクトル空間W1,W2について、
・V=W1+W2
かつ
・dim(V)=dimW1+dimW2
が成り立つならば、
実ベクトル空間Vは、部分ベクトル空間W1 ,W2の直和に分解される
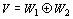
3.
実ベクトル空間Vが、その部分ベクトル空間W1 , W2 , …,Wkの直和に分解される
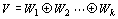
ならば、
dim(V)=dimW1+dimW2+…+dimWk
4.
実ベクトル空間Vと、その部分ベクトル空間 W1 ,W2 , …,Wk について、
・V=W1+W2+…+Wk
かつ
・dim(V)=dimW1+dimW2+…+dimWk
が成り立つならば、
実ベクトル空間Vは、部分ベクトル空間 W1 , W2 , …,Wkの直和に分解される
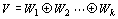
(reference)
日本数学会編集『岩波数学辞典(第三版)』 岩波書店、1985年、項目210線形空間(pp.570-576)
線形代数のテキスト
ホフマン・クンツェ『線形代数学I』培風館、1976年、2.3基底と次元定理5-6(pp.46-9)。
砂田利一『現代数学への入門:行列と行列式』2003年、§5.3-d(p.179).
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、1.3ベクトル空間(pp.14-6)。
佐武一郎『線形代数学(第44版)』裳華房、1987年、Ⅲベクトル空間§6ベクトル空間の公理化(p.115)。
志賀浩二『数学30講シリーズ:線形代数30講』朝倉書店、1988年、13講ベクトル空間へ(pp.85-7);14講ベクトル空間の例と基本概念(pp.88-90)。
藤原毅夫『理工系の基礎数学2:線形代数』岩波書店、1996年、4.1線形空間と写像(p.91)。
斎藤正彦『線形代数入門』東京大学出版会、1966年、第4章§4線形部分空間(p.107-112)。
数理経済学のテキスト
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、§3.1ベクトル空間とは何か(p.105)。
→[トピック一覧:部分ベクトル空間の次元]
→線形代数目次・総目次