距離空間のあいだの連続写像：トピック一覧　　

　・連続性の定義：点での連続性/点集合上連続/リプシッツ連続/一様連続性　
　・連続性の性質：点列の収束との関係/開集合の逆像との関連　　
　・連続写像一般の性質：合成写像の連続性　
　・コンパクト空間上の性質：連続写像のコンパクト不変性/コンパクト空間上の連続写像の一様連続性　
　・連結な空間上の性質：連続写像の連結不変性　　　

　※距離空間の間の写像の諸概念：写像の定義/極限の定義/連続写像の性質　
　※距離空間の間の連続写像の具体例：1変数関数の連続性/2変数関数の連続性/ n変数関数の連続性/
　　　　　　　　　　　　　　　　　　　　実数値関数の連続性/ベクトル値関数の連続性　
　※距離空間の間の連続写像の一般化：位相空間のあいだの連続写像　　
　→参考文献/総目次

定義： 距離空間のあいだの写像が点Aで連続

はじめに
読むべき
定義

「写像『f：E→Y』は、点Aで連続であるcontinuous」とは、
　次の3条件がすべて満たされることを言う。
　(1)　f (A)が定義されていること
　(2)　
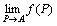
　　　　が存在すること。　
　　　　つまり、P→Aで、f (P)が収束すること。　　　
　(3)
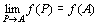
　　　が成立すること。
　　　つまり、f (P) → f (A)（P→A）　　　
※上記条件の一つでも満たされていないとき、
　「f：E→Y」は点Aで不連続であるdiscontinuousという。

cf.集合上で連続/一様連続性

具体例：1変数関数/2変数関数/ n変数関数/実数値関数/ベクトル値関数

一般化：位相空間上の写像

[文献]
矢野『距離空間と位相構造』1.1.3(p.14)

舞台設定

厳密には、
「距離空間から距離空間への写像が点Aで連続」の定義は、以下の手順で設定された舞台の上でなされる。
Step1：2つの集合を用意する(集合ならなんでもよい)。
　　　　　　・集合X
　　　　　　・集合Y
Step2：集合Xの部分集合のひとつ(Xの部分集合ならなんでもよい)を選んで、集合E と名づける。
　　　　つまり、「E⊂X」　　
Step3：「集合Xの部分集合E」から「集合Y」への写像 f を用意。
　　　　つまり、「 f：E→Y 」　
Step4：集合Xに距離d_X を定めて、集合X上に、距離空間( X , d_X )を設定。
Step5：集合Yに距離d_Y を定めて、集合Y上に、距離空間( Y , d_Y )を設定。
Step6：「集合Xの部分集合E」上の動点を、Pと名づける。
　　　　「集合Xの部分集合E」上の定点を、Aと名づける。　
　　　　　　　　つまり、「P, A∈E⊂X」　　

厳密な
定義
ε-δ論法

「写像『f：E→Y』は、点Aで連続であるcontinuous」とは、
　任意の正数εに対して、ある正の実数δが存在して、
　　「 d_X( P, A )＜δ ⇒ d_Y ( f (P), f (A) )＜ε 」
　を成り立たせる、ということ。
この定義を、論理記号で表せば、
（∀ε>０）（∃δ>０）（∀P∈E ）（ d_X( P, A )＜δ ⇒ d_Y ( f (P), f (A) )＜ε ）
　　* d_X( P, A )は、距離空間( X , d_X )でのPとAとの距離を、
　　　d_Y ( f (P), f (A) )は、距離空間( Y , d_Y )上の f (P)とf (A)との距離を表す。

* 「P→Aのときfが収束する」の定義では、 ０＜d_X( P, A )＜δ であった。
　　つまり、「極限」では、P＝Aを除外して考えたが、
　　　　　「連続」ではP＝Aを除外しないことになる。

[文献]
ルディン『現代解析学』4.5(p.83)。
松坂『集合・位相入門』6章§1D定理3(pp.240-2)。

厳密な
定義
近傍

「写像『f：X→Y』は、点Aで連続であるcontinuous」とは、
　距離空間( Y , d_Y )上の点f (A)の任意の「ε近傍 U_ε( f (A) )」に対して、
　ある「Xにおける点Aのδ近傍U_δ(A)」が存在して、
　　　　　 f ( U_δ(A)) ⊂ U_ε( f (A) )　
　を満たす
ということ。
この定義を別の表現でいうと、
　任意の（どんな）正の実数εに対して（でも）、ある正の実数δが存在して、
　　　　　　　　「　 f ( U_δ(A) ) ⊂ U_ε( f (A) )　　」
　　　　すなわち「　P∈U_δ(A) ならば、f (P) ∈U_ε( f (A) )」
　を成り立たせる、
ということ。
この定義を、論理記号で表せば、
（ ∀ U_ε( f (A) ) ）（∃U_δ(A)）（ f ( U_δ(A) ) ⊂ U_ε( f (A) ) ）　
（∀ε>０）（∃δ>０）（ f ( U_δ(A) ) ⊂ U_ε( f (A) ) ）　
（∀ε>０）（∃δ>０）（∀P∈E）（ P∈U_δ(A) ⇒ f (P) ∈U_ε( f (A) )）　
となる。

[文献]
松坂『集合・位相入門』6章§1D定理3(pp.240-2)。

二階堂『現代経済学の数学的方法』2章§13定理1(p.91)

活用例

→[トピック一覧：距離空間のあいだの連続写像]
→総目次

定義：距離空間のあいだの写像が集合E上で連続

はじめに
読むべき
定義

「写像『f：E→Y』が、集合Eで連続であるcontinuous」とは
　　集合Eに属す各点でfが連続である
ことをいう。　　

cf.点での連続性/一様連続性
具体例：1変数関数/2変数関数/ n変数関数/実数値関数/ベクトル値関数/　

一般化：位相空間上の写像

[文献]
ルディン『現代解析学』4.5(p.83);
矢野『距離空間と位相構造』1.1.3(p.14)

『岩波数学辞典』項目92距離空間I.一様連続 (pp.255).

舞台設定

厳密には、
「距離空間から距離空間への写像が集合Eで連続」の定義は、
　以下の手順で設定された舞台の上でなされる。
Step1：2つの集合を用意する(集合ならなんでもよい)。
　　　　　　・集合X
　　　　　　・集合Y
Step2：集合Xの部分集合のひとつ(Xの部分集合ならなんでもよい)を、選んで、
　　　　　　集合E　
　　　　と名づける。　
　　　　つまり、「E⊂X」　　
Step3：「集合Xの部分集合E」から「集合Y」への写像 f を用意。
　　　　つまり、「 f：E→Y 」　
Step4：集合Xに距離d_X を定めて、集合X上に、距離空間( X , d_X )を設定。
Step5：集合Yに距離d_Y を定めて、集合Y上に、距離空間( Y , d_Y )を設定。
Step6：「集合Xの部分集合E」上の動点を、Pと名づける。
　　　　「集合Xの部分集合E」上の定点を、Aと名づける。　
　　　　　　　　つまり、「P, A∈E⊂X」　　

厳密な
定義
ε-δ論法

「写像『f：E→Y』が、集合Eで連続であるcontinuous」とは
　　「集合Eに属す点Aをひとつ選んで固定した上で、
　　　任意の正数εに対して、ある正数δをとると、
　　　　　 d_X( P, A )＜δ ⇒ d_Y ( f (P), f (A) )＜ε 　　　…(1)
　　　が成り立つ」
　　ということが、すべての点A∈Eについてもいえるということ。
論理記号で表せば、すなわち
　( ∀ A∈E ) ( ∀ε＞0 ) ( ∃δ＞0 ) ( ∀ P∈E ) ( d_X( P, A )＜δ ⇒ d_Y ( f (P), f (A) )＜ε )
※ここで、(1)を満たすδを全てのA∈Eに対して共通に選ぶ必要はないことに注意。
　「fがE上で連続」と言った場合、A∈Eの選び方で(1)を満たすδが変わってもよい。
　これに対して、
　(1)を満たすδを全てのA∈Eに対して共通に選べる、
　A∈Eの選び方によらず、εだけに対応して (1)を満たすδを一様に選べることを意味する概念は、
　一様連続性。

厳密な
定義
近傍

「写像『f：X→Y』は連続であるcontinuous」とは、
　集合Xに属す限りで任意の点Aと、
　距離空間( Y , d_Y )上の点f (A)の任意の「ε近傍 U_ε( f (A) )」に対して、
　ある「Xにおける点Aのδ近傍U_δ(A)」が存在して、
　　　　　 f ( U_δ(A)) ⊂ U_ε( f (A) )　
　を満たす
ということ。
この定義を別の表現でいうと、
　集合Xに属す限りで任意の点Aと、任意の（どんな）正の実数εに対して、
　　　ある正の実数δが存在して、
　　　　　　　　「　 f ( U_δ(A) ) ⊂ U_ε( f (A) )　　」
　　　　すなわち「　P∈U_δ(A) ならば、f (P) ∈U_ε( f (A) )」
　を成り立たせる、
ということ。
この定義を、論理記号で表せば、
(∀A∈X ) （∀ U_ε( f (A) ) ）（∃U_δ(A)）（ f ( U_δ(A) ) ⊂ U_ε( f (A) ) ）　
(∀A∈X )（∀ε>０）（∃δ>０）（ f ( U_δ(A) ) ⊂ U_ε( f (A) ) ）　
(∀A∈X )（∀ε>０）（∃δ>０）（∀P∈E）（ P∈U_δ(A) ⇒ f (P) ∈U_ε( f (A) )）　
となる。

→[トピック一覧：距離空間のあいだの連続写像]
→総目次

定理：距離空間のあいだの写像の点における連続性の、点列の収束への言い換え　

→ 1変数関数の連続の、数列の収束への言い換え
→ 2変数関数の連続の、点列･数列の収束への言い換え
→ n変数関数の連続の、点列･数列の収束への言い換え
→ ベクトル値関数の連続の、点列の収束への言い換え　

[文献]
矢野『距離空間と位相構造』定理1.5(p.14):証明付
松坂『集合・位相入門』6章§1D定理3(pp.240-2):証明付。
神谷浦井『経済学のための数学入門』定義4.3.3(p.139)
二階堂『現代経済学の数学的方法』2章§13(p.90)

要旨

距離空間から距離空間への写像の連続性は、
収束点列の像の点列の収束に、
言いかえられる。　

舞台設定

この定理は、以下の手順で設定された舞台の上で成り立つ。
Step1：2つの集合を用意する(集合ならなんでもよい)。
　　　　　　・集合X
　　　　　　・集合Y
Step2：「集合X」から「集合Y」への写像 f を用意。
　　　　つまり、「 f：X→Y 」　
Step4：集合Xに距離d_X を定めて、集合X上に、距離空間( X , d_X )を設定。
Step5：集合Yに距離d_Y を定めて、集合Y上に、距離空間( Y , d_Y )を設定。
Step6：「集合X」上の動点を、Pと名づける。
　　　　「集合X」上の定点を、Aと名づける。　
　　　　　　　　つまり、「P, A∈X」　　

定理

次の命題P,Qは互いに言い換え可能である。
つまり、命題P⇔命題Q。

命題P：
　写像「 f：X→Y 」は、点Aで連続　

命題Q：
　距離空間( X , d_X )上のどんな点列{ P_i }={ P₁ , P₂ , P₃,…}についてであれ、
　　　点列{ P_i }={ P₁ , P₂ , P₃,…}が点Aに収束する限り、
　その点列の各項 P₁ , P₂ , P₃,…を写像fによりY上に写した像の点列　
　　　　{ f ( P_i ) }={ f ( P₁ ), f ( P₂ ) , f ( P₃ ) ,… }
　は
　点Aを写像fによりY上に写した像 f ( A ) に収束する。
　つまり、
　　距離空間( X , d_X )上の任意の点列{ P_i }={ P₁ , P₂ , P₃,…}について、
　　　　　　　　　　　　　　　P_i→A (i→∞) ならば、f ( P_i)→ f ( A ) (i→∞)　
　論理記号で表すと、
　　　（∀{ P_i }）（ P_i→A (i→∞) ⇒ f ( P_i)→ f ( A ) (i→∞) ）

※なぜ？
　　関数の収束の定義と、関数の連続性の定義を見比べたうえで、
　　関数の収束と点列の収束の関連性についての定理を、関数の連続性向けに修正。　

活用例

→[トピック一覧：距離空間のあいだの連続写像]
→総目次

定理：距離空間のあいだの連続写像と、開集合の逆像　

Cf.位相空間における連続写像定義/ベクトル値関数のケース　

[文献]
ルディン『現代解析学』4.8(p.83):証明付。
神谷浦井『経済学のための数学入門』定義4.5.3(p.150)
二階堂『現代経済学の数学的方法』2章§13定理3(p.93):証明付

舞台設定

この定理は、以下の手順で設定された舞台の上で成り立つ。
Step1：2つの集合を用意する(集合ならなんでもよい)。
　　　　　　・集合X
　　　　　　・集合Y
Step2：「集合X」から「集合Y」への写像 f を用意。
　　　　つまり、「 f：X→Y 」　
Step4：集合Xに距離d_X を定めて、集合X上に、距離空間( X , d_X )を設定。
Step5：集合Yに距離d_Y を定めて、集合Y上に、距離空間( Y , d_Y )を設定。

定理

次の命題P,Qは互いに言い換え可能である。
つまり、命題P⇔命題Q。

命題P：
　写像「 f：X→Y 」は、X上連続。　

命題Q：
　距離空間( Y , d_Y )上の任意の開集合O_Yに対して、
　　O_Yの fによるX上の逆像 f^-1( O_Y )は、距離空間( X , d_X )上の開集合となる。　

※なぜ？→ルディン『現代解析学』4.8(p.83)　

→[トピック一覧：距離空間のあいだの連続写像]
→総目次

定理：距離空間のあいだの合成写像の連続性

要旨

二つの連続写像の合成写像は連続。

設定

この定理は、以下の手順で設定された舞台の上で成立する。
Step1：3つの集合を用意する(集合ならなんでもよい)。
　　　　　　・集合X
　　　　　　・集合Y
　　　　　　・集合Z
Step2：集合Xの部分集合のひとつ(Xの部分集合ならなんでもよい)を、選んで、
　　　　　　集合E　
　　　　と名づける。　
　　　　つまり、「E⊂X」　　
Step3：「集合Xの部分集合E」から「集合Y」への写像 f を用意。
　　　　つまり、「 f：E→Y 」　
Step4：「集合Yの部分集合 f (E)」から「集合Z」への写像 g を用意。
　　　　つまり、「 g：f (E)→Z 」　
Step5：集合Xに距離d_X を定めて、集合X上に、距離空間( X , d_X )を設定。
Step6：集合Yに距離d_Y を定めて、集合Y上に、距離空間( Y , d_Y )を設定。
Step7：集合Zに距離d_Z を定めて、集合Z上に、距離空間( Z , d_Z )を設定。
Step8：「集合Xの部分集合E」上の動点を、Pと名づける。
　　　　「集合Xの部分集合E」上の定点を、Aと名づける。　
　　　　　　　　つまり、「P, A∈E⊂X」　　

[具体例]
1変数関数の合成関数の連続性/ベクトル値関数のケース
[一般化]
位相空間のあいだの写像の合成写像の連続性　

[文献]
ルディン『現代解析学』4.7(p.84):証明付;
矢野『距離空間と位相構造』定理4.1(p.14):証明付;

定理

写像『f：E→Y』が点A∈E⊂Xで連続、
かつ
写像『g：f (E)→Z』が点f (A)∈f (E)⊂Yで連続
ならば、
合成写像 g〇f (P)= g ( f (P)))は、点A∈E⊂Xで連続。

※

具体例：1変数関数の合成関数の連続性、2変数関数の合成関数の連続性、

→[トピック一覧：距離空間のあいだの連続写像]
→総目次

定義：距離空間のあいだのリプシッツ連続写像　

Cf.位相空間における連続写像定義

[文献]
矢野『距離空間と位相構造』例1.12(p.15)例4.7(p.130)

舞台設定

この定義は、以下の手順で設定された舞台の上でなされる。
Step1：2つの集合を用意する(集合ならなんでもよい)。
　　　　　　・集合X
　　　　　　・集合Y
Step2：「集合X」から「集合Y」への写像 f を用意。
　　　　つまり、「 f：X→Y 」　
Step4：集合Xに距離d_X を定めて、集合X上に、距離空間( X , d_X )を設定。
Step5：集合Yに距離d_Y を定めて、集合Y上に、距離空間( Y , d_Y )を設定。

定義

→[トピック一覧：距離空間のあいだの連続写像]
→総目次

定義：距離空間のあいだの写像の一様連続性 uniformly continuous

舞台設定

「距離空間から距離空間への写像の一様連続性」の定義は、
　以下の手順で設定された舞台の上でなされる。　
Step1：2つの集合を用意する(集合ならなんでもよい)。
　　　　　　・集合X
　　　　　　・集合Y
Step2：「集合X」から「集合Y」への写像 f を用意。
　　　　つまり、「 f：X→Y 」　
Step3：集合Xに距離d_X を定めて、
　　　　集合X上に距離空間( X , d_X )を設定。
Step4：集合Yに距離d_Y を定めて、
　　　　集合Y上に距離空間( Y , d_Y )を設定。
Step5：「集合Xの部分集合E」上の動点を、Pと名づける。
　　　　「集合Xの部分集合E」上の定点を、Aと名づける。
　　　　　　　　つまり、「P, A∈X」　　

cf.E上で連続：δが各A∈E毎にちがっていてもよい。
[具体例]1変数関数の一様連続性/2変数関数の一様連続性/ n変数関数の一様連続性/ベクトル値関数の一様連続性　
[一般化]実数値関数の一様連続性
[文献]
『岩波数学辞典』項目92-I一様連続 (pp.255).
松坂『集合・位相入門』6章§3A(p.253)。
ルディン『現代解析学』4.18(p.88)。
斉藤『数学の基礎:集合･数･位相』5.4.1 (p.167);
神谷浦井『経済学のための数学入門』4.6(p.159):近傍で表現。
矢野『距離空間と位相構造』4.1(p.130)

定義

「写像『f：X→Y』はX上で一様連続uniformly continuousである」とは、
　任意の正数εに対して、ある正数δをとると、
　　「d_X (P, A)＜δを満たす限りで任意の『Xの元』」P,Aについて、d_Y ( f (P), f (A) )＜εが成り立つ　
ということ。
論理記号で表せば、すなわち、
( ∀ε＞0 ) ( ∃δ＞0 ) ( ∀A∈X ) ( ∀P∈X ) ( d_X( P, A )＜δ ⇒ d_Y ( f (P), f (A) )＜ε)
※δが、各A∈Dに対して一様にとれることを意味している点が、重要。

近傍を
用いた
定義

「写像『f：X→Y』はX上で一様連続uniformly continuousである」とは、
　任意の正数εに対して、ある正数δをとると、
　　「すべての『Xの元』Aについて、 f ( U_δ(A) ) ⊂ U_ε( f (A) )　」

　を成り立たせる、
ということ。　　　
この定義を、論理記号で表せば、
　　（∀ε>０）（∃δ>０）(∀A∈X )（ f ( U_δ(A) ) ⊂ U_ε( f (A) ) ）　
となる。[神谷浦井『経済学のための数学入門』4.6(p.159)]

性質

・写像『f：X→Y』 がX上で一様連続ならば、f はX上で連続。　　
・一般には、写像『f：X→Y』がX上で連続だからといって、X上で一様連続だとは限らない。
・Xがコンパクトならば、写像『f：X→Y』がXで一様連続であることと連続であることは同値
　→詳細　

否定命題

「写像『f：X→Y』はX上で一様連続でない」とは、
　 ( ∃ε＞0 ) ( ∀δ＞0 ) ( ∃A∈D ) ( ∃P∈D ) ( d_X( P, A )＜δ かつ d_Y ( f (P), f (A) )≧ε )
　　　　　　　　　　[杉浦『解析入門I』�W章積分§4連続関数の可積分性-定理4.1証明(4.4)(p. 226)]

※

関連事項：点での連続性/X上で連続(δが各A∈X毎にちがってもよい)　　　
具体例 ：1変数関数の一様連続性/2変数関数の一様連続性/ n変数関数の一様連続性/　

→[トピック一覧：距離空間のあいだの連続写像]
→総目次