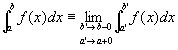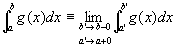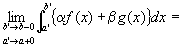1変数関数についての広義積分の性質
【トピック一覧】
・定理:区間I上広義可積ならIに含まれる任意の区間で広義可積/ 区間加法性 / 線形性 / 広義積分可能な関数の積 / 単調性
・定理:絶対可積・絶対収束/条件収束/三角不等式
【関連ページ:1変数関数の広義積分について】
前:有限区間における非有界関数の広義積分の定義・無限区間における広義積分定義
次:向き付き広義積分・ 積分関数(不定積分)・解析学の基本定理・収束条件・ガンマ関数ベータ関数
cf. 1変数関数の定積分、2変数関数の広義積分、n変数関数の広義積分
→総目次
定理:
[高木『解析概論』104:証明なし; 吹田新保『理工系の微分積分学』115:証明なし.]
関数fが有限区間Iにおいて広義積分可能、
または
関数fが無限区間Iにおいて広義積分可能とすると、
Iに含まれる任意の区間で広義積分可能。
cf.この定理の定積分版、
定理:区間加法性
[高木『解析概論』104:証明なし・広義積分に向きをつけた上で;小平『解析入門I』178:証明は176:向きの付かない広義積分で;吹田新保『理工系の微分積分学』115:証明なし;.]
定積分の区間加法性は、広義積分でも成り立つ。
すなわち、 a<b<cに対して、
広義積分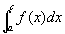 が収束しているならば、
が収束しているならば、
[すなわち、関数f(x)が開区間(a,c)において広義積分可能ならば、]
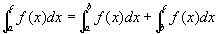
応用例:
(証明) 小平『解析入門I』178は、広義積分の定義から明らかであるとしている。
定理:線形性
[小平邦彦『解析入門I』178-180; 吹田新保『理工系の微分積分学』115:証明なし;]
定積分の線形性は、広義積分でも成り立つ。
すなわち、
広義積分
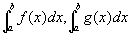
が収束しているならば、
任意の定数α、βに対して、
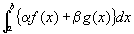
も収束し、
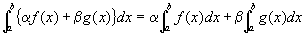
(証明の沿革)
広義積分も、定義にまで遡ると、普通のリーマン定積分であるから、普通のリーマン定積分の線形性を適用できる。
(開区間(a,b)における広義積分である場合の説明: 小平『解析入門I』179)
Step1:
開区間(a,b)における広義積分が定義されているということは、すでに以下が前提されている。
1. 閉区間[a,b]において、その境界点a,bだけが特異点である。
だから、それを除いた区間、
すなわち、任意のa',b' (a< a'<b'<b )に対して[a',b']
において、f(x) , g(x)は有界かつリーマン積分可能である。…①
2. 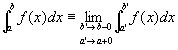
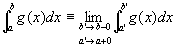
という有限の極限値が存在する。 …②
Step2:
①より、②で問題にされている
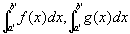
は、普通のリーマン定積分なのだから、普通のリーマン定積分の線形性が成り立って、
任意の定数α、βに対して、
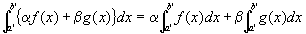 …③
…③
Step3:
ここで、a'→ a+0、b'→b-0としても、a'=a, b'=bとなるところまで行かないから、
①より、[a',b']において、f(x) , g(x)は有界かつリーマン可積であり、
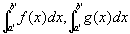
は、普通のリーマン定積分なのだから、普通のリーマン定積分の線形性が成り立つ。
よって、a'→ a+0、b'→b-0としても、③は成り立つ。
つまり、
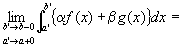
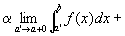
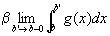
これを、広義積分の記号を用いて書きかえると、
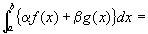
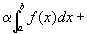
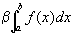
([a,b]の中に特異点を含んだ広義積分である場合の説明)
定理:広義積分可能な関数の積
[高木『解析概論』108;吹田新保『理工系の微分積分学』115:証明なし;.]
ある区間で関数f,gがそれぞれ広義積分可能でも、積f gもその区間で広義積分可能であるとは限らない。
例:
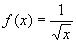
は、(0,1]で広義積分可能だが、積f(x)・f (x)=1/xは、(0,1]で広義積分可能ではない。
cf. 定理:積分可能な関数の積:「閉区間[a,b]で有界な関数f,gがそこで積分可能なら、積f gも積分可能。」
Question:普通のリーマン定積分可能な関数の積は可積なのに、広義積分可能な関数の積が可積とは限らないのは、どこが、どう違うからか?
定理:広義積分の単調性
cf.向きのついた積分の単調性
定積分の単調性は、広義積分でも成り立つ。
すなわち、f(x),g(x)が区間(a,b)で高々有限個の点を除いて連続な関数であって、
広義積分
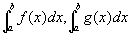
が収束しており、
区間(a,b)で常に f(x)≦g(x) なら、
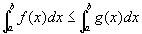
等号が成り立つのは、f,gが連続なら、つねに、f(x)=g(x) である場合だけ。
応用例:、
[小平邦彦『解析入門I』179-180:証明付き; 高木『解析概論』108:証明なし;]
(証明)
定義:絶対可積・絶対収束
[杉浦『解析入門』292;高木『解析概論』106;吹田新保『理工系の微分積分学』117;.小平『解析入門I』185]
1. ある区間で、関数f(x)が広義積分可能である(「f(x)の広義積分が収束する」)からといって、
|f(x)|も広義積分可能である(「|f(x)|の広義積分が収束する」)とは限らない。
[つまり、普通の定積分の性質「fが積分可能ならば、|f|も積分可能」は、広義積分では成り立たない。]
2. ある区間で|f(x)|が広義積分可能である(「|f(x)|の広義積分が収束する」)とき、
その区間で「f(x)は絶対可積である」、「f(x)の広義積分は絶対収束する」という。
定義:条件収束
[吹田新保『理工系の微分積分学』117;.]
収束しているが絶対収束でない広義積分は、条件収束するという。
定理:広義積分に関する三角不等式
cf.定積分に関する三角不等式
[小平『解析入門I』178-180; 杉浦『解析入門』292;高木『解析概論』106; 吹田新保『理工系の微分積分学』117;.]
|f(x)|が広義積分可能であるなら、
(すなわち「f(x)が絶対可積である」「f(x)の広義積分が絶対収束する」なら)
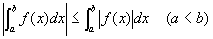
これは、有限区間の広義積分でも無限区間の広義積分でも成り立つ
[高木『解析概論』106; 小平『解析入門I』180]
(証明) 定積分に関する三角不等式 から。[小平『解析入門I』180]
(reference)
日本数学会編集『岩波数学辞典(第三版)』 岩波書店、1985年、202項積分法(pp.520-525)。
小平邦彦『解析入門I』 (軽装版)岩波書店、2003年 pp.178-180。
高木貞治『解析概論 改訂第三版』岩波書店、1983年、p. 104-5.
杉浦光夫『解析入門』岩波書店、1980年、pp.290-295次元の広義積分の定義と収束条件。
吹田・新保『理工系の微分積分学』学術図書出版社、1987年。pp.113-120.
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.90-93.
青本和彦『岩波講座現代数学への入門:微分と積分1』岩波書店、1995年、138-143.軽く説明。
矢野健太郎・田代嘉宏『社会科学者のための基礎数学 改訂版』裳華房、p.117-8.
和達三樹『理工系の数学入門コース1:微分積分』岩波書店、1988年、pp.98-103.