広義積分の計算1:解析学の基本定理
【トピック一覧】
・有限区間での広義積分についての解析学の基本定理
・無限区間での広義積分についての解析学の基本定理
【関連ページ:1変数関数の広義積分について】
1変数関数の広義積分について:
前:広義積分定義(有限区間・無限区間)・性質・向き付き広義積分・積分関数(不定積分)
次: 収束条件・ガンマ関数ベータ関数
cf. 1変数関数の定積分、2変数関数の広義積分、n変数関数の広義積分
→参考文献一覧・総目次
定理:有限区間での広義積分についての
微分積分学の基本定理
fundamental theorem of differential and integral calculus
解析学の基本定理fundamental theorem of calculus
[高木『解析概論』109:解析学の基本定理の広義積分への拡張;小平『解析入門I』180-183.]
cf.定積分の範囲での解析学の基本定理
・閉区間I=[a,b]において、
有限個の不連続点 c1 , c2 , …, cm ( a≦ c1 < c2 < …< cm ≦b )を除いて、f(x)が連続、
かつ、
・閉区間I=[a,b]で連続(な関数G(x))、かつ、 c1 , c2 , …, cm を除いて微分可能で導関数がf(x)となる
関数G(x)が存在するならば、
(すなわち不連続点を除いて原始関数が存在し、かつ
f(x)の不連続点でもその原始関数が連続であるなら、
その原始関数の一つをG(x)と置くということ、)
広義積分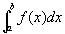 は収束し、
は収束し、
その値を下式で計算できる。

(証明:第1段階) [小平『解析入門I』180-181;高木『解析概論』109.]
「閉区間 [a,b]において、両端(x=a,b)を除いてf(x)が連続、
かつ
閉区間 [a,b] で連続・両端(x=a,b)を除いて微分可能で導関数がf(x)となるG(x)が存在するならば、
広義積分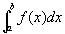 は収束し、その値を
は収束し、その値を

で計算できる。」
を示す。
仮定の整理:開区間 (a,b)においてf(x)が連続。…①
開区間 (a,b)においてG'(x)=f(x) (すなわち(a,b)でG(x)はf(x)の原始関数)…②
G(x)は、閉区間 [a,b] で連続 (つまり開区間 (a,b)で連続かつx=aで右連続、x=bで左連続)…③
Step1:
a<a'<b'<bを満たす限りにおいて任意の a', b' を選び、閉区間 [a', b'] をつくる。
①より、閉区間 [a', b'] においてf(x)は連続(定理より、そこでリーマン可積でもある)。…④
Step2:
②④より、
定積分
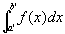
にたいして、定積分の範囲内での解析学の基本定理を適用可能。よって、
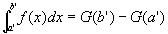 …⑤
…⑤
Step3:
a'→a+0、b'→b-0 としても、 a<a'<b'<bを満たすので、
閉区間 [a', b']において、f(x)について④が成り立ち、定積分について⑤も成り立つ。
つまり、
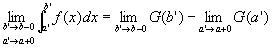 …⑥
…⑥
Step4:
③で、G(x)はx=aで右連続、x=bで左連続とされていた。
右連続・左連続の定義にしたがって、数式に書きなおすと、
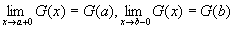
これを使って、⑥を書きかえると、
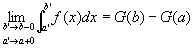 …⑦
…⑦
Step5:
⑦の左辺は、広義積分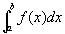 の定義に他ならない。
の定義に他ならない。
よって、⑦は、①~③の仮定の下でなら、
広義積分 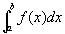 が収束し、
が収束し、
下式で計算できることを意味している。

(証明:第2段階)
証明:第1段階のごく一部を変えるだけで、
「閉区間 [a,b]において、両端(x=a,b)の一方を除いてf(x)が連続、
( つまり、半開区間 (a,b] ないし [a,b)でf(x)が連続 )
かつ
閉区間 [a,b]で連続・f(x)の不連続点を除いて微分可能で導関数がf(x)となるG(x)が存在するならば、
広義積分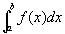 は収束し、その値を
は収束し、その値を

で計算できる。」
を示せる(だから省略)。
(証明:第3段階) [小平『解析入門I』182;高木『解析概論』109.]
「閉区間 [a,b]において、有限個の不連続点c1 , c2 , …, cm (a=c1 < c2 < …< cm=b)を除いて、f(x)が連続、
かつ
閉区間 [a,b] で連続かつ、c1 , c2 , …, cm を除いて微分可能で導関数がf(x)となるG(x)が存在する
ならば、
広義積分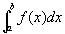 は収束し、その値を
は収束し、その値を

で計算できる。」
を示す。
仮定の整理:
・a=c1 < c2 < …< cm=b …(0)
・k=1,…,m-1のすべてについて(つまり、不連続点で仕切られた小区間のすべてについて)、
以下が成り立つ。
開区間 ( ck ,ck+1 ) においてf(x)が連続。…①
開区間 ( ck ,ck+1 )においてG'(x)=f(x) (すなわち( ck ,ck+1 )でG(x)はf(x)の原始関数)…②
G(x)は、閉区間 [ck ,ck+1] で連続 (つまり開区間 (ck ,ck+1)で連続かつx= ckで右連続、x= ck+1で左連続)…③
Step1:
仮定①②③より、各閉区間 [ck ,ck+1](k=1,…,m-1)について、証明:第1段階を適用可能。
これを適用すると、k=1,…,m-1のすべてについて、下式左辺の広義積分が右辺に収束する。
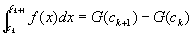 …④
…④
Step2:
広義積分の区間加法性を繰り返し用いて、k=1,…,m-1のすべてについて足し合せると、
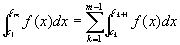
右辺に④を代入すると、
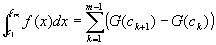
={G(c2)-G(c1)}+{ G(c3)-G(c2)}+{ G(c4)-G(c3)}+…+{ G(cm)-G(cm-1)}
= G(cm) -G(c1) (この二項以外はすべてキャンセルされていく)
…⑤
(0)で a=c1 、cm=b とされていたから、
⑤は以下のように書きかえられる。

(証明:第4段階) [小平『解析入門I』182;高木『解析概論』109.]
「閉区間 [a,b]において、有限個の不連続点c1 , c2 , …, cm (a<c1 < c2 < …< cm<b)を除いて、f(x)が連続、
かつ
閉区間 [a,b] で連続かつ、c1 , c2 , …, cm を除いて微分可能で導関数がf(x)となるG(x)が存在する
ならば、
広義積分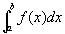 は収束し、その値を
は収束し、その値を

で計算できる。」
を示す。
仮定の整理:
・a<c1 < c2 < …< cm<b …(0)
・k=1,…,m-1のすべてについて(つまり、不連続点で仕切られた小区間のすべてについて)、
以下が成り立つ。
開区間 ( ck ,ck+1 ) においてf(x)が連続。…①
開区間 ( ck ,ck+1 )においてG'(x)=f(x) (すなわち( ck ,ck+1 )でG(x)はf(x)の原始関数)…②
G(x)は、閉区間 [ck ,ck+1] で連続 (つまり開区間 (ck ,ck+1)で連続かつx= ckで右連続、x= ck+1で左連続)…③
・閉区間 [a, c1]において、c1を除いて、f(x)が連続
閉区間 [a, c1] で連続かつ、c1を除いて、f(x)が微分可能で導関数がf(x)となるG(x)が存在する…④
・閉区間 [cm , b]において、c1 を除いて、f(x)が連続
閉区間 [cm , b] で連続かつ、c1を除いて、f(x)が微分可能で導関数がf(x)となるG(x)が存在する…⑤
Step1:
仮定①②③より、閉区間 [c1 ,cm]について、証明:第3段階を適用可能。
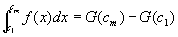 …⑥
…⑥
Step2:
仮定④⑤より、閉区間 [a,c1] [cm,b] について、証明:第2段階を適用可能。
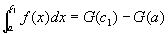 …⑦
…⑦
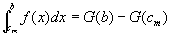 …⑧
…⑧
Step3:
広義積分の区間加法性を繰り返し用いると、
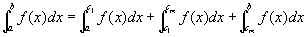
この右辺に⑥⑦⑧を代入して、
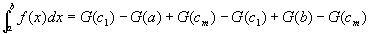
=G(b)-G(a)
定理:無限区間での広義積分についての
微分積分学の基本定理fundamental theorem of differential and integral calculus
解析学の基本定理fundamental theorem of calculus
[小平『解析入門I』182-183.]
cf.定積分の範囲での解析学の基本定理
無限区間 (a,+∞)で定義された関数f(x)について考える。
a<tを満たすtを一つ選び開区間(a,t)をつくる。
どんな風にtをとって、開区間(a,t)をつくったとしても、
・開区間(a,t)において高々有限個の点を除いてf(x)が連続、
かつ、
・広義積分 は収束している
は収束している
とする。
このとき、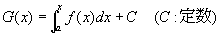
は、無限区間 (a,+∞)で連続なxの関数となる。
極限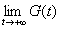
が存在するならば、
広義積分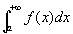 は収束している
は収束している
広義積分その値を下式で計算できる。
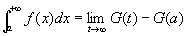
※疑問:きわめてtautological.
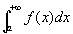 の収束は、
の収束は、
極限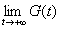 が存在しなければならないというが、
が存在しなければならないというが、
この極限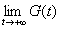 が存在するということは、G(x)の定義、広義積分
が存在するということは、G(x)の定義、広義積分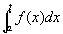 の定義から、すなわち、
の定義から、すなわち、
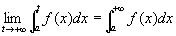
が存在するということになる。
だから、
「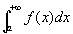 が収束するならば、
が収束するならば、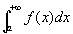 が収束する」などという
が収束する」などという
ヘンな説明になっているのでは?。
(reference)
小平邦彦『解析入門I』 (軽装版)岩波書店、2003年、180-183.;。
高木貞治『解析概論 改訂第三版』岩波書店、1983年、109;
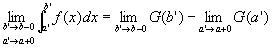 …⑥
…⑥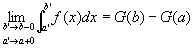 …⑦
…⑦