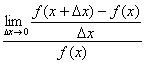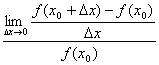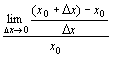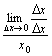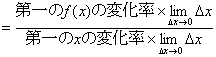1変数関数の導関数の計算公式　：　トピック一覧

　・定数の微分公式　
　・k次関数（kは整数）の微分公式/k次関数（kは実数全般）の微分公式 
　・対数関数の微分公式/指数関数の微分公式
　・絶対値の対数の微分公式/関数の絶対値の対数の微分公式(応用：対数微分法/相対変化率/弾力性)

　・関数の和の微分公式/関数の定数倍の微分公式/関数の積の微分公式/関数の商の微分公式
　・合成関数の微分公式chain rule/逆関数の微分公式/媒介関数による微分公式 

　※1変数関数の微分関連ページ：
　　微分の定義 / 高階導関数
　　ロルの定理・平均値の定理 / テイラーの定理 / テイラー展開・マクローリン展開 / 極大極小
　※1変数関数関連ページ：
　　1変数関数とその属性　/　極限の定義　/　無限小解析　/　連続性　/　微分　/　リーマン積分　
　※多変数関数の微分関連ページ：
　　2変数関数の偏微分 / 2変数関数の全微分 / n変数関数の偏微分 / n変数関数の全微分
　　1変数m値ベクトル値関数の微分法 / n変数m値ベクトル値関数の微分法
　※総目次

定理：絶対値の対数の微分

　(　log|x|　)’＝1／x ,　　x∈R　, x≠0　　　　　　　[『高等学校微分積分』p.62]　

　※なぜ？→証明　　

定理：関数の絶対値の対数の微分　logarithmic derivative 

　(　log| f(x) |　)’＝ f ' (x)／ f (x)　、ただしf(x)≠0、f(x)が微分可能なxの範囲において。 [『高等学校微分積分』p.62]

　※なぜ？→証明　
　※活用例：対数微分法、相対変化率　　　

関数の対数の微分の応用(1)――対数微分法　



　対数微分法とは、

　　 f(x)=(xを用いた具体的な数式)

　という関数を微分するときに、

　両辺の絶対値の対数をとって微分する計算法のこと。


　【具体的な手順】　


　　手順1. 両辺の絶対値の対数をとる。　　
　　　　　　　log| f(x) |　＝　log|(xを用いた具体的な数式)|　　
　　
　　手順2. 両辺をそれぞれxで微分する。左辺には関数の対数の微分を適用。
　　　　　　(　log| f(x) |　)’＝　(　log | (xを用いた具体的な数式)|　)’　　　
　　　　　　　　f ' (x)／f(x)＝log|(xを用いた具体的な数式)|をxで微分してでてきた具体的な式　
　　　　　　　　　　　　　　　　　ただしf(x)≠0、f(x)が微分可能なxの範囲において。　

　　手順3. 整理　　f '(x)＝ f(x)・「log|(xを用いた具体的な数式)|をxで微分してでてきた具体的な式」　

　※積の形の関数、根号を含む関数など対数をとると簡単な形になる関数で、有効。　　
　※対数微分法の利用例1 / 対数微分法の利用例2：ベキ関数の微分公式
　


[文献]
　・竹之内『経済・経営系数学概説』p. 93
　・和達『微分積分』p.51

　・『高等学校　微分積分』p.63 

　　

→[トピック一覧：導関数計算公式]　　
→総目次　

　関数の対数微分の応用(2)――　相対変化率　the relative rate of change　　



　関数の絶対値の対数の微分公式　　　

　　　　( log| f(x) | )’＝f ' (x)／f(x) 　　　　
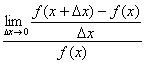
　　　　　　　　　　　≡相対変化率　

　は、

　 f(x)のxにおける相対変化率the relative rate of change of f(t)　
　　　　　　　　　増加率　
　　　　　　　　　成長率
　などの名称で、

　経済学に頻繁に登場。

　経済学では、これを「変化率」と呼ぶこともあるようだけど、　　

　数学書では、「変化率」という言葉は微分係数と同義に用いられることもあるので、

　この経済学の言い回しは、混乱のもとになるような気がするのですが・・・。　


[文献]
　・竹之内『経済・経営系数学概説』p. 93

　・Goldstein,et.al, Calculus and Its Applications, pp.280-284.




※相対変化率の具体例－自動車の速度計・加速度計　
　相対変化率の具体例―価格の変化
　対数微分法・相対変化率の活用例―[実質GNP]＝[名目GNP]／[物価水準] とすると、[実質GNP成長率]＝[名目GNP成長率]－[物価上昇率]
　対数微分法・相対変化率の活用例：素朴な貨幣数量説を対数微分を用いて増加率の関係に変形　
　対数微分法・相対変化率の活用例：コブダグラス型生産関数を時間について微分　　　　　
　
→[トピック一覧：導関数計算公式]　　
→総目次　

関数の対数微分の応用(3)――　弾力性　


　二通りの定義がある模様。

　どちらも等しくなるので、心配無用。

　【共通の定義】


　　関数f(x)のx=x0における弾力性
　　η(x0)＝[x=x0におけるf(x)の変化率]／[x=x0におけるxの変化率]　　　　　　　　　　

　　ところが、「変化率」の定義の違いから、
　　以下に見るように、二種類の「弾力性」定義が生じてしまう。　　　　　　　　　　　

　　二種類の「変化率」は、お互いに値もことなるが、
　　そこから定義される二種類の「弾力性」については、
　　どういうわけか、どちらの値も、等しくなる。　　　　　　　　　　　

　　だから、正確に言えば、
　　　　変化率の異なった二つの定義によって、
　　　　ただ一様に定義された「弾力性」について、二つの解釈がなされうる、
　　ということになるだろう。




[文献]
　・高橋『経済学とファイナンスのための数学』pp.66-67.
　・奥野正寛・鈴村興太郎『ミクロ経済学』p.278.

　・Goldstein,et.al, Calculus and Its Applications, pp.280-284.



　【「弾力性」の定義１】


　　　　　[　Goldstein,et.al, Calculus and Its Applications, pp.282-284. 　　　]
　　[a-1]　x=x0におけるf(x)の変化率　　　　　
　　　　　　変化率を、前項の相対変化率で定義する。　　　
　　　　　　単位は、「x一単位あたりで何パーセントの変化率」になる。　
　　　　　ゆえに、
　　　　　x = x0におけるf(x)の変化率は、
　　　　 (　log | f (x0) |　)’＝ f ' (x0)／f (x0)　 　　　
　　　　　　　　　　　≡　
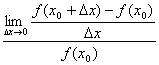
　　　　　　で定義される。　　　　　
　　　　　　　　ここで、分子は、x = x0でのfの微分係数であり、
　　　　　　　　　x = x0付近でのxのわずかな挙動に対する、f(x0)の反応幅の比率を、
　　　　　　　　（実際にはxを単位量も動かしていないのだが）
　　　　　　　　　xを単位量動かしたとしたと想定した場合のf(x0)の増分で表示している。
　　　　　　　　（瞬間速度は、「瞬間」に進んだ距離を、
　　　　　　　　　　実際には為されていない1「時間」に進んだとした想定のもとでの距離で
　　　　　　　　　　表示する。これと同じ。）
　　　　　　　　　したがって、このf(x0)の増分が、
　　　　　　　　　そのときのf(x0)の何パーセントにあたるのかを、
　　　　　　　　　　相対変化率の全体は表している。

　　[a-2]　x=x0におけるxの変化率　　　　　　　　　　　　
　　　　　x = x0 におけるxの変化率は、f(x)=xとおいたときの相対変化率
　　　　 (　log | f (x0) |　)’＝ f ' (x0)／f (x0)　 　
　　　　　　　　　　　　　　
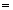
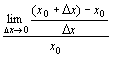
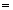
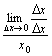
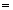
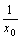
　　　　　　で定義される。　　　　　
　　　　　　　x = x0 付近でのxのわずかな挙動に対する、xの反応幅の比率は、当然1。
　　　　　　xを単位量動かしたとしたと想定した場合のxの増分は当然１。
　　　　　　したがって、このxの増分が、そのときの　x = x0 の何パーセントにあたるのかを意味する、
　　　　　　　x = x0 におけるxの相対変化率は1／x0　。　　　
　　　　　　
　　　[b]　x=x0におけるf(x)の弾力性　　　　　
　　　　関数f(x) の　x = x0 における弾力性
　　　　　　　＝[　x = x0 におけるf(x)の変化率]／[　x = x0 におけるxの変化率]　
　　　　　　　　
　　　　　　　　
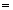
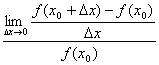
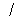
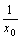
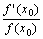
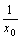
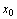
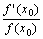
　　　　　　　　　　　∵絶対値の対数の導関数、関数の絶対値の対数の導関数（相対変化率）　　
　　　　　　　
　　 　　　

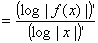
【「弾力性」の定義2】　


　　　　　　[　奥野・鈴村『ミクロ経済学』p.278、伊藤『ミクロ経済学』pp.31-37;pp.54-56.]　　

　　a.　x = x0におけるf(x)及びxの変化率　　　　　

　　　　変化率を、[変化による増分]／[変化前の量]で、定義する。　　　

　　　　したがって、x = x0におけるf(x)の変化率は、　　

　　　　　　

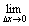
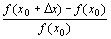
　　　　　　x = x0におけるxの変化率は、　　　　　　　　　　　

　　　　　　　　　　　　　　　　　

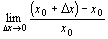
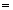
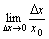
　　　　一般に、x = x0におけるf(x), xの変化率じたいは、概念としては描けるものの、

　　　　(　f(x)　がx = x0で連続なら　)　0に収束するだけで、関数の性格について何も語らない。

　　　　しかし、この二つの変化率の比である弾力性は、関数の性格を捉える上で有力な手がかりとなる。　　

　　b.　x = x0におけるf(x)の弾力性　　　　　

　　　　関数f(x)のx = x0における弾力性

　　　　η(x0)＝[x = x0におけるf(x)の変化率]／[x = x0におけるxの変化率]　　　　　　　　　　　　　　　
　　　　　　　　　
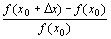
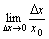
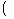
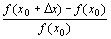
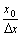
　　　　　　　　　　　∵極限の商　　
　　　　　　　　　　　　　　
　　　　　　　　　
　　　　　　　
　　　　　　　　
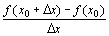
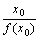
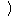
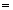
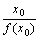
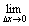
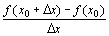
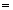
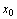
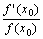
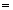
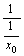
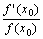
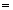
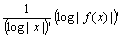
　　　　　　　　　　　∵絶対値の対数の導関数、関数の絶対値の対数の導関数（相対変化率）　　
　　　　　　　　　

　　

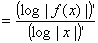
　　　　なぜ、異なった変化率の定義から出発しても、同一の弾力性定義へ行き着くのか？
　　　　　　　第一の変化率：相対変化率（「x一単位あたりで何パーセントの変化率」）、
　　　　　　　第二の変化率：[変化による増分]／[変化前の量]（増分が0に限りなく近いのでゼロ）
　　　　　　　この二つの関係をよくみると、
　　　　　　　　　　第一の変化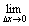率×＝第二の変化率　　　　　　　
　　　　　　　　つまり、　　

　　　　　　　　　　第一の[x = x0におけるf(x)の変化率]

　　　　　　　　　　
　　　　　　　　　　　　　　　　　

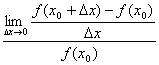
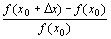
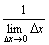
　　　　　　　　　　第二の[x = x0におけるf(x)の変化率]　　　

　　　　　　　　　　　　　　　　　

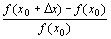
　　　　　　　　なので、
　　　　　　　　　　第一のf(x)の変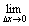化率×＝第二のf(x)の変化率　。　


　　　　　　　　第一の[x = x0におけるxの変化率]：1／x0　　　　　　　　　　　　

　　　　　　　　第二の[x = x0におけるxの変化率]：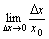　　　　
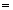
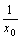
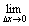
　　　　　　　　なので、
　　　　　　　　　　　　　第一のxの変化率×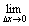＝第二のxの変化率　
　　　　　　　　ゆえに、　　　
　　　　　　　　第二の弾力性＝[第二のf(x)の変化率]／[第二のxの変化率]　　　
　　　　　　　　　
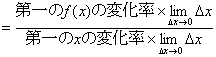
　　　　　　　　＝(第一のf(x)の変化率)/(第一のxの変化率)　∵lim⊿xが分母分子で打ち消しあう　　　　
　　　　　　　　＝第一の弾力性　　　
　
→[トピック一覧：導関数計算公式]　　
→総目次　

（reference）

吉田耕作・栗田稔・戸田宏『平成元年3/31文部省検定済高等学校数学科用　高等学校　微分・積分　新訂版』啓林館、pp.49-52.
竹之内脩『経済・経営系数学概説』新世社、1998年、pp.92-93。
和達三樹『微分積分』岩波書店、1988年、pp.47-52.
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.49-55.
Chiang, Fundamental Methods of Mathematical Economics: Third Edition, McGraw Hill,1984. pp.155-173.
Goldstein,Lay,Schneider, Calculus and Its Applications (International Editions): Eight Edition, Prentice Hall, 1999.　
中谷巌『入門マクロ経済学第三版』日本評論社、1993年、p.110;162;356　
岩田一政『国際経済学』新世社、1990、pp.79-80.
岩田一政『現代金融論』新世社、1992、p.23.
奥野正寛、鈴村興太郎『ミクロ経済学』岩波書店、1985年、p.80;84;90:108;168;180;197:199;278.
伊藤元重『ミクロ経済学』日本評論社、1992年、pp.31-37;pp.54-56.
縄田和満『EXCELによる回帰分析入門』1998年、pp.6-7.