相対変化率の具体例1：
価格の変化という具体例のなかで、導関数、対数微分、相対変化率が何を意味するのかを、みていく。

[設定]　　
　　　t:　　時間（単位：年）、
　　　f(t):　t時点における米1キロの価格（単位：円）、
　　　g(t):　t時点におけるフロッピーディスク1枚の価格（単位：円）
とする。f(t), g(t)は全ての範囲で微分可能で、常に正(０にはならない)とする。
[導関数の意味]　　
　　・このとき、f(t)の導関数　　　
　　　　　　f ' (t) ≡　　　　
　　　の意味を考えてみよう。
　　　まず、分子f(t+��t )−f(t)は、
　　　　　　　　t時点の米1キロの価格が、瞬間的な時間の長さ��t経過後、
　　　　　　　　何円上昇したのか
　　　を示している。
　　　これを、瞬間的な時間の長さ��tで割ることは、
　　　　　　　　tの単位あたり、ここでは年あたりに、換算すること
　　　を意味する。

　　　ゆえに、f(t)の導関数全体は、t時点における米1キロの「瞬間」的価格変化が　　
　　　　　　　　　　　　　「年率換算」すると何円の上昇幅となるのかを意味している。　　　
　　　単位は、円／年。
　　・g'(t) ≡　　　　
　　　も、同様に、
　　　t時点におけるフロッピーディスク一枚の「瞬間」的価格変化が　　
　　　　　　　　　「年率換算」すると何円の上昇幅となるのかを意味すると解釈できる。　　　
　　　瞬間的変化を年率換算するのは奇妙に思えるかもしれないが、
　　　自動車の速度計がそのときの「瞬間」的速度を時速換算で表示していることを考えてみれば、
　　　それほど奇妙でもないだろう。
　　　単位は、円／年。
[変化率の意味]　　
　　　　すると、　　　
　　　　(log|f(t)|)’＝f ' (t)／f(t)　　　　
　　　　≡　　　　　　　　　　　　　
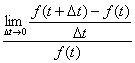
　　　　は、t時点における、
　　　　　　　　「時価」(円)= f(t)に対する、
　　　　　　　　「瞬間」的価格変化の「年率」上昇幅換算額(円)=f ' (t)の比率(単位なし)に他ならない。　
　　　　たとえば、
　　　　　　t = t_０　において、f(t_０)=400, g(t_０)=100, f ' (t_０)=−50, g' (t_０)=−50　であるとする。　
　　　　これは、t₀時点における、米1キロの「時価」が400円、[f(t_０)]
　　　　　　　　　　　　　　　　FD一枚の「時価」が100円、[g(t_０) ]
　　　　　　　　　　　　　　　　米1キロの「瞬間」的価格変化が「年率換算」−50円 [ f ' (t_０) ]
　　　　　　　　　　　　　　　　FD一枚の「瞬間」的価格変化が「年率換算」−50円 [ g' (t_０) ]
　　　　であることを意味している。
　　　　このとき、
　　　　　米1キロとフロッピーディスクの価格低下の著しさを、
　　　　　f ' (t_０), g ' (t_０)の−50円から、同一であると、判断するのは、おかしい。
　　　　同じ50円の価格低下でも、
　　　　　　　　　400円から50円下がるのと、
　　　　　　　　　100円から50円下がるのでは、
　　　　後者のほうが価格低下著しいと見るのが、自然であろう。
　　　　そこで、価格変化の著しさを比較する場合に、「変化率」が用いられることになる。
　　　　t₀時点における米1キロの価格変化率（価格上昇率）：(log|f(t)|)’＝f ' (t)／f(t)＝−12.5%　　
　　　　t₀時点におけるFD一枚の価格変化率（価格上昇率）：(log|g(t)|)’＝g ' (t) ／g(t)＝−50%　　

→戻る