相対変化率の具体例0：
自動車の速度・加速度という具体例のなかで、
導関数、対数微分、相対変化率が何を意味するのかを、みていく。
1.自動車の速度計
　　　　　　[『基礎解析』pp.92-93;p.98,『高等学校微分積分』pp92-93]
[設定]　　
　t:　　時間（単位：hour）、
　f(t):　t時点までに自動車が走行した距離（単位： km）
とする。f(t)は全ての範囲で微分可能で、常に正(０にはならない)とする。
[導関数の意味]　　
　・このとき、f(t)の導関数　　　
　　　　　f ' (t) ≡　　
　　の意味を考えてみよう。

　　まず、分子f(t+��t )−f(t)は、t時点から、瞬間的な時間の長さ��t経過後までに、
　　　　　　　　　　　　　　何キロ自動車が進んだのかかを示している。　　
　　これを、瞬間的な時間の長さ��tで割ることは、
　　　　　　　　　　　　　　tの単位あたり、ここではhourあたりに、換算することを意味する。
　　ゆえに、f(t)の導関数全体は、t時点において自動車が瞬間的に進んだ距離が　　
　　　　　　　　　　　　　「時間当たりに換算」するとどれだけの距離となるのかを意味している。　　　
　　単位は、キロ／時。
　　これが、自動車の速度メーターが示す瞬間的な時速である。
　　速度メーターは、そのときの「瞬間」的速度を「時速」換算で表示している。
　　奇妙なことだが、我々はこの事態を普段受け入れている。

[相対変化率の意味]　　
　　すると、
　　(　log|f(t)|　)’＝f ' (t)／f(t)　
　　≡　
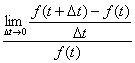
　　は、t時点における、
　　　　これまでの走行距離 (km)= f(t)に対する、
　　　「瞬間」的速度の「時速」換算値=f ' (t)の比率(単位なし)となる。
　　つまり、今のペースで1時間走ったとしたら、
　　今まで走った距離の何パーセントになるんだろう？
　　と、計算していることになる。
　　もちろん、このような指標が使われることはまずない。
2.加速度計　　[『基礎解析』pp.92-93;p.98,『高等学校微分積分』pp92-93]
　　　t:　　時間（単位：hour）、
　　　f(t):　t時点での自動車の速度（単位： km／時）
　　　とする。f(t)は全ての範囲で微分可能で、常に正(０にはならない)とする。
[導関数の意味]　　
　　　・このとき、f(t)の導関数　　　
　　　　　　　f ' (t) ≡　　　
　　　　の意味を考えてみよう。

　　　　まず、分子f(t+��t )−f(t)は、t時点から、瞬間的な時間の長さ��t経過後までに、
　　　　　　　　　　　　　　時速何キロ分、自動車の速度が増加したのか
　　　　　　　　　　　　　（速度メーターがどれだけふれたのか）を示している。　　　　　　
　　　　これを、瞬間的な時間の長さ��tで割ることは、
　　　　　　　　　　　　　　　　tの単位あたり、ここではhourあたりに、換算することを意味する。
　　　　ゆえに、f(t)の導関数全体は、t時点における自動車の瞬間的加速が　　
　　　　　　　　　　「時間当たりに換算」するとどれだけの加速となるのかを意味している。　　　
　　　　単位は、キロ／時^２。
　　　　これが、自動車に加速度計がついているなら示すであろう瞬間的な加速度である。
[相対変化率の意味]　　
　　　　すると、　　　
　　　　(　log|f(t)|　)’＝f ' (t)／f(t)　　　　
　　　　≡　　　　　　　　　　　　　　
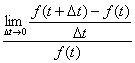
　　　　は、t時点における速度 (km／時)= f(t)に対する、
　　　　　　t時点における「瞬間」的加速度の「毎時」換算値=f ' (t)の比率(単位なし)となる。　　
　　　　つまり、今のペースで1時間加速し続けたとしたら、
　　　　現在の時速の何パーセントにあたるんだろう？
　　　　一時間に進む距離は現在のペースから何パーセント増えるのだろう、
　　　　と、計算していることになる。

→戻る