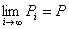空間Rⁿにおける点列の収束･極限―定義：トピック一覧　

　・定義：点列/部分列/距離空間(Rⁿ,d)での点列の収束･極限点/ユークリッド空間上での点列の収束･極限点/有界な点列
　・定理：点列の収束と座標ごとの収束の関係
　※Rⁿにおける点列の関連ページ：収束点列の極限とベクトル和・スカラー倍　　　
　※列とその収束・極限の関連ページ：R上の数列/R²上の点列/点列一般　
　cf. n変数関数の極限定義　
　※参考文献・総目次　　

定義：空間Rⁿ上の点列

(はじめに読むべき定義)
　すべての自然数1,2,3,…の各々に対して、空間Rⁿ上の点P₁ , P ₂ , P ₃ ,…を定めたものを、
　空間Rⁿ上の点列と呼ぶ。

[文献]
『岩波数学辞典』項目58D族列(p.158);
神谷浦井
『経済学のための数学入門』定義4.3.1(p.136);
小平
『解析入門I』p60;
杉浦
『解析入門I』I§4(p.38)

(厳密な定義)
　各項が空間Rⁿ上の点である列、
　つまり、「X⊆Rⁿとした、写像 ( 関数 )φ：N→ X 」を点列と呼ぶ。

(記法)
　　　　　
　{ P_i }_i∈N　　　{ P₁ , P₂ , P₃ , … }　　　{ P_i }_i=1,2,3,…　
　かなり略して、{ P_i }

(意図)　数列をn次元へ拡張したものと理解すればよい。

(ベクトルとの関連)
　「空間Rⁿ上の点」とは、「実数をn個並べた組(x₁ , x₂ ,…, x_n)」のこと。
　したがって、「空間Rⁿ上の点P₁ , P ₂ , P ₃ ,…」とは、
　　実際のところ、「n個並べた組(x₁₁ , x₁₂ ,…, x_1n), (x₂₁ , x₂₂ ,…, x_2n), (x₃₁ , x₃₂ ,…, x_3n),…」であり、
　これは、「実n次元数ベクトルx₁=(x₁₁ , x₁₂ ,…, x_1n), x₂=(x₂₁ , x₂₂ ,…, x_2n), x₃=(x₃₁ , x₃₂ ,…, x_3n),…」といっても同じ。
　だから、「平面R²上の点列」は、「実n次元数ベクトルの列」に他ならない。

(他の点列)　R上の数列、R²上の点列、点列一般

定義：Rⁿ上の点列の部分列sub-sequence

(はじめに読むべき定義)
空間Rⁿ上の点列{ P₁ , P₂ , P₃ , …}　が与えられているとする。　　　
この点列の項P₁ , P₂ , P₃ , P₄ , P₅ ,…(可算無限個)から、
その一部の項(可算無限個)を抜き出し、順序を保ったまま並べた点列
　　　　たとえば、
　　　　　　P₁, P₃, P₅, P₇,…　
　　　　　　P₁₀, P₁₁, P₁₂, P₁₃, P₁₄, P₁₅,…　　
　　　　　　P₀, P₁₀, P₁₈, P₂₀, P₄₅, P₁₀₀,…　　
　　　　など　　　　　　
を、点列{P₁,P₂,P₃,…}の部分列と呼ぶ。　

[文献]

『岩波数学辞典』項目58-D族・列(p.158);

矢野
『距離空間と位相構造』1.1.2点列の収束(pp.10-11);

神谷浦井
『経済学のための数学入門』4.3節(p.141);

(少しかたい定義)
点列{P_i}_i∈Nの部分列とは、I⊂Nにたいする{P_i}_n∈Iのこと。

(記法)
点列{P_i}_i∈Nの部分列は、
　{P_{i (k)} }　
　{P_ik }　
などと表す。
kは、部分列のなかで何番目の項にあたるかを、
i _(k) は、もとの点列で何番目の項だったのかを表している。
例えば、

もとの点列：

P₀ ,

P₁ ,

P₂ ,

P₃ ,

P₄ ,

P₅ ,

…

　　部分列：

P₁ ,

P₃ ,

P₅ ,

P₇ ,

P₉ ,

…

↑

↑

↑

↑

↑

P_i(1) ,

P_i(2) ,

P_i(3) ,

P_i(4) ,

P_i(5) ,

…

つまり、点列{P_i}_i∈Nの部分列{P_i(k) }の添数i_(k)は、数列{ i _k } _k∈Nとなっており、
　この数列{ i _k } _k∈Nは、狭義単調増加i₁ ＜i ₂ ＜i ₃ ＜…である。

(他の点列の部分列)
　数列の部分列、R²上の点列の部分列、一般の集合上の点列の部分列　

→[トピック一覧：Rⁿにおける点列]
→総目次

定義：距離空間(Rⁿ,d)上の点列の収束と極限点

　　　　※「距離空間(Rⁿ,d)上の」の意味がわからない場合→ユークリッド空間上の点列の収束･極限を参照。
　　　　　　なにもことわらずに、「Rⁿ上の点列」といえば、それは「ユークリッド空間上の点列」のこと。
　　　　　　なお、距離空間(Rⁿ,d)は、ユークリッド空間の一般化。→距離空間のイントロダクション　　

(直感的な説明)

点列{P_i}が、点Pに収束するとは、iが大きくなるにつれて、点列をなす各点P_iが点Pに「近づく」ことである。
しかし、この「近づく」とは、どういうことなのか―よく考えてみると、はっきりしない。
これについて明確化するために、点列の収束は、次のように、少々面倒くさいかたちで定義されることになる。

(はじめによむべき定義)

[文献]
『岩波数学辞典』項目166E(pp436);
矢野『距離空間と位相構造』1.1.2(p.10);
松坂『集合・位相入門』6章§1-C(pp.238-9) ;
高木『解析概論』p.14.;
小平『解析入門I』§1.6(p.60);
吹田新保『理工系の微分積分学』p.155　

空間Rⁿに距離dを定めて設定した距離空間 ( Rⁿ, d ) 上の点列
　　　{P₁ , P₂ , P₃ , …}＝{ (x₁₁ , x₁₂ ,…, x_1n), (x₂₁ , x₂₂ ,…, x_2n) , (x₃₁ , x₃₂ ,…, x_3n),… }
が、点P (x₁ , x₂ ,…, x_n)に収束するとは、　　　　　
　　数列{ d ( P₁ , P ) , d ( P₂ , P ) , d ( P₃ , P ) ,… }が０に収束すること、　
　　すなわち、d ( P_i , P ) →０ ( i→∞ )　
　　　　　　　　　　
　　が成り立つこと
を言う。
また、点列{P₁ , P₂ , P₃ , …}が点Pに収束するとき、
Pを極限limit、極限点などと呼ぶ。

(厳密な定義)

松坂『集合・位相入門』6章§1-C(pp.238-9) ;
斉藤『数学の基礎：集合・数・位相』4.5.11(p.131);
神谷浦井『経済学のための数学入門』定義4.3.2(p.137) ;
杉浦『解析入門I』1章§4(pp.38-40)

空間Rⁿに距離dを定めて設定した距離空間 ( Rⁿ, d ) 上の点列
　　　{P₁ , P₂ , P₃ , …}＝{ (x₁₁ , x₁₂ ,…, x_1n), (x₂₁ , x₂₂ ,…, x_2n) , (x₃₁ , x₃₂ ,…, x_3n),… }
が、点P (x₁ , x₂ ,…, x_n)に収束するとは、
　任意のε> ０に対して、ある自然数Nが存在し、
　　「N以上のあらゆるの自然数iに対して、d ( P_i , P ) <ε」
　　ないし「N以上のあらゆるの自然数iに対して、P_i が点Pのε近傍に属す」
　を成立させるということ。
点列{P₁ , P₂ , P₃ , …} が点Pに収束するとき、
Pを極限limit、極限点などと呼ぶ。

(論理記号による表現)

距離空間 ( Rⁿ, d )上の点列{P_i}が、点P∈Rⁿに収束するとは、　　　
　　( ∀ε＞０ )　(∃N∈N)　(∀i∈N)　( i≧N⇒ d ( P_i , P ) <ε)　
　　( ∀ε＞０ )　(∃N∈N)　(∀i∈N)　( i≧N⇒ P_i∈U_ε(P) )　
　　( ∀U_ε(P) )　(∃N∈N)　(∀i∈N)　( i≧N⇒ P_i∈U_ε(P) )　　
点列{ P_i }が点Pに収束するとき、Pを極限limit、極限点などと呼ぶ。

杉浦『解析入門I』1章§4(pp.38-40)

(記法)

　　P_i→ P　（i→∞）　
　　　
　と記す。　

※（はじめに読むべき定義）と（厳密な定義）は同じもの

（はじめに読むべき定義）d ( P_i , P ) →０ ( i→∞ )　　
は、数列の収束の厳密な定義より、次のように言い換えても同じこと。
　　　　　　　　(∀ε>０) (∃N∈N) (∀i∈N) ( i≧N⇒| d ( P_i , P )−０ |< ε) 　…(1)　
距離dの定義より、d ( P_i , P )≧０だから、| d ( P_i , P )−０ |< ε⇔d ( P_I , P )< ε　
したがって、(1)は、　
（厳密な定義） (∀ε>０) (∃N∈N) (∀i∈N) ( i≧N⇒ d ( P_i , P )< ε)　
に言い換えても同じこと。

(他の収束･極限概念)

数列の収束と極限値、R²上の点列の収束･極限、一般の距離空間上の点列の収束･極限

n変数関数の極限定義　

→[トピック一覧：Rⁿにおける点列]
→総目次

定義：ユークリッド空間Rⁿ上の点列の収束と極限点

　　　※ここでは、特に、距離がユークリッド距離で定義されたユークリッド空間Rⁿの上で、点列の収束について考える。

(はじめに読むべき定義)

[文献]
『岩波数学辞典』項目92D(pp.254-255); 項目166E(pp436)
矢野『距離空間と位相構造』1.1.2(p.10);
松坂『集合・位相入門』6章§1-C(pp.238-9) ;
小平『解析入門I』§1.6(p.60);
吹田新保『理工系の微分積分学』p.155

設定

ここでは、
　空間Rⁿにユークリッド距離dを与えることで設定されたユークリッド空間(Rⁿ,d)
という舞台の上で「点列の収束」の定義をみる。

定義

ユークリッド空間(Rⁿ,d)上の点列
　　　{ P₁ , P₂ , P₃ , … }＝{ (x₁₁ , x₁₂ ,…, x_1n), (x₂₁ , x₂₂ ,…, x_2n) , (x₃₁ , x₃₂ ,…, x_3n),… }
が、点P(x₁ , x₂ ,…, x_n)に収束するとは、
　　数列{ d ( P₁ , P ) , d ( P₂ , P ) , d ( P₃ , P ) ,… }が０に収束すること、　
　　すなわち、
　　　　　　
が成り立つことをいい、
これを、
または、P_i→P　（i→∞）
で表す。
また、点列{ P₁ , P₂ , P₃ , … }が点Pに収束するとき、Pを極限limit、極限点などと呼ぶ。

(厳密な定義)

[文献]
高木『解析概論』p.14.;
志賀『位相への30講』第2講(pp.10-15);
松坂『集合・位相入門』6章§1-C(pp.238-9) ;
斉藤『数学の基礎：集合・数・位相』4.5.11(p.131);
神谷浦井『経済学のための数学入門』定義4.3.2(p.137) ;
杉浦『解析入門I』1章§4(pp.38-40)

設定

ここでは、
　空間Rⁿにユークリッド距離dを与えることで設定されたユークリッド空間(Rⁿ,d)
という舞台の上で「点列の収束」の定義をみる。

定義

ユークリッド空間(Rⁿ,d)上の点列{P₁ , P₂ , P₃ , …}が、点P (x₁ , x₂ ,…, x_n)に収束するとは、
　任意のε> 0に対して、ある自然数Nが存在し、
　　　　「N以上のあらゆる自然数iに対して、
　　　　　　　　　」
　　　　　ないし
　　　　「N以上のあらゆる自然数iに対して、P_i(x_i1 , x_i2 ,…, x_in)が点Pのε近傍
　　　　　　　
　　　　　に属す」
　を成立させることをいい、
これを、
または、P_i→ P　（i→∞）
で表す。

(論理記号による表現)

P_i→P　（i→∞）

⇔ (∀ε＞０) (∃N∈N) (∀i∈N)　
　　　　　　　
　　ないし、
　　(∀ε＞０) (∃N∈N) (∀i∈N)　　
　　　　　

杉浦『解析入門I』1章§4(pp.38-40)

（ベクトル表現）

設定

「ユークリッド空間(Rⁿ,d)上の点列{P₁ , P₂ , P₃ , …}の収束」の定義は、ベクトルでも表現できる。
ベクトルで表された「ユークリッド空間(Rⁿ,d)上の点列{P₁ , P₂ , P₃ , …}の収束」の定義は、
以下の手順で設定された舞台上でなされる。　
Step1： n次元空間Rⁿを用意する。
　　　　　　　　* n次元空間Rⁿとは、 実数をn個並べた組 (x₁,x₂,…,x_n ) をすべてあつめた集合。
　　　　　　　　　すなわち、「実数全体の集合R」のそれ自身へのn回の直積
　　　　　　　　　　　　　　　R×R×…×R={ (x₁ , x₂ ,…, x_n) | x₁∈Rかつx₂∈Rかつ…かつx_n∈R }　
　　　　　　　　　これは、実n次元数ベクトルをすべて集めた集合でもある。
Step2：Rⁿにたいして、通例のベクトルの加法・スカラー乗法を定義して、実n次元数ベクトル空間Rⁿを設定。
Step3：実n次元数ベクトル空間Rⁿにたいして、「自然な内積(標準内積)・」「ユークリッドノルム‖‖」を定義して、
　　　　ノルム空間（ Rⁿ, ‖‖ ）を設定。　　　
Step4：ノルム空間（ Rⁿ, ‖‖ ）にたいして、ユークリッドノルムから定めた距離d(x, y)=‖x−y‖を定義して、
　　　　ユークリッド空間(Rⁿ,d)を設定。
Step5：ユークリッド空間(Rⁿ,d)上の定点をP=(x₁ , x₂ ,…, x_n)　と名づける。　

定義

ユークリッド空間(Rⁿ,d)上の点列
　　　{ P₁ , P₂ , P₃ , … } ＝ { (x₁₁ , x₁₂ ,…, x_1n) , (x₂₁ , x₂₂ ,…, x_2n) , (x₃₁ , x₃₂ ,…, x_3n) , … }
が、点P (x₁ , x₂ ,…, x_n)　に収束するとは、
　　数列{ d ( P₁ , P ) =‖P₁ −P‖, d ( P₂ , P )=‖P₂ −P‖ , d ( P₃ , P )=‖P₃ −P‖ ,… }が０に収束すること、　
　　すなわち、　
　　　　
が成り立つこと、をいう。
数列の収束の定義にまで遡ると、
ユークリッド空間(Rⁿ,d)上の点列
　　　{ P₁ , P₂ , P₃ , … } ＝ { (x₁₁ , x₁₂ ,…, x_1n) , (x₂₁ , x₂₂ ,…, x_2n) , (x₃₁ , x₃₂ ,…, x_3n) , … }
が、点P (x₁ , x₂ ,…, x_n)に収束するとは、
　　( ∀ε＞０ )　(∃N∈N)　(∀i∈N)　( i≧N⇒ d ( P_i , P )= ‖P_i −P‖<ε)　　

（図解1）

※

以上は、空間Rⁿ上の点列の収束と極限点の定義における距離dに、ユークリッド距離を与えるだけで得られる。

※

ユークリッド距離と位相的に同値である距離をR²に与えてつくった距離空間でどうなるか
　　→志賀『位相への30講』第11講(pp.81-2)

→[トピック一覧：Rⁿにおける点列]
→総目次

定理：ユークリッド空間Rⁿ上の点列の収束と座標ごとの収束の関係　

設定

この定理は、以下の手順で設定された舞台上で成立する。
Step1： n次元空間Rⁿを用意する。
　　　　　　　　* n次元空間Rⁿとは、 実数をn個並べた組 (x₁,x₂,…,x_n ) をすべてあつめた集合。
　　　　　　　　　すなわち、「実数全体の集合R」のそれ自身へのn回の直積
　　　　　　　　　　　　　　　R×R×…×R={ (x₁ , x₂ ,…, x_n) | x₁∈Rかつx₂∈Rかつ…かつx_n∈R }　
　　　　　　　　　これは、実n次元数ベクトルをすべて集めた集合でもある。
Step2：空間Rⁿにユークリッド距離を与えて、ユークリッド空間(Rⁿ, d )を設定。　
Step3：ユークリッド空間(Rⁿ,d)上の定点をP=(x₁ , x₂ ,…, x_n) と名づける。
Step4：ユークリッド空間(Rⁿ,d)上の点列を{ P₁ , P₂ , P₃ , … }と名づける。　、
　　　　　　　　*点列{ P₁ , P₂ , P₃ , … }の各点P_iはn個の実数の順序対( x_i1 , x_i2…, x_in )を表す。
　　　　　　　　　つまり、{ P₁ , P₂ , P₃ , … }＝{ (x₁₁ , x₁₂ ,…, x_1n), (x₂₁ , x₂₂ ,…, x_2n) , (x₃₁ , x₃₂ ,…, x_3n),… }
　　　　　　　　　とも書ける。

定理

以下の二つの命題は同値である。
[命題1]
　点列{ P₁ ,P₂ ,P₃ ,…}={ (x₁₁ , x₁₂ ,…, x_1n), (x₂₁ , x₂₂ ,…, x_2n) , (x₃₁ , x₃₂ ,…, x_3n),… }が、
　点P=( x₁ , x₂ ,…, x_n )へ収束する。
　つまり、　
　　　　　　　
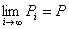
[命題2]
　・点列{P₁,P₂,P₃,…}={(x₁₁ , x₁₂ ,…, x_1n), (x₂₁ , x₂₂ ,…, x_2n) , (x₃₁ , x₃₂ ,…, x_3n),…}　
　　　の各点の第１成分だけを取り出して並べた数列{ x₁₁ , x₂₁, x₃₁,… }が、　
　　　　点Pの第１成分x₁に収束し、
　かつ
　・点列{P₁,P₂,P₃,…}={ (x₁₁ , x₁₂ ,…, x_1n), (x₂₁ , x₂₂ ,…, x_2n) , (x₃₁ , x₃₂ ,…, x_3n) ,…}　
　　　の各点の第2成分だけを取り出して並べた数列{ x₁₂ , x₂₂, x₃₂,… }が、　
　　　　点Pの第2成分x₂に収束し、
　かつ
　　：
　かつ
　・点列{P₁,P₂,P₃,…}={(x₁₁ , x₁₂ ,…, x_1n), (x₂₁ , x₂₂ ,…, x_2n) , (x₃₁ , x₃₂ ,…, x_3n),…}
　　　の各点の第n成分だけを取り出して並べた数列{ x_1n , x_2n, x_3n,… }が、
　　　　　点Pの第n成分x_nに収束する。
　つまり、
　　　
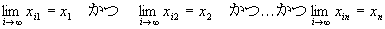
※なぜ？→証明　

[文献]
高木『解析概論』p.14:R²上のユークリッド空間;
小平『解析入門I』§1.6-d(p.60) :R²上のユークリッド空間;
矢野『距離空間と位相構造』例1.9(p.12) :Rⁿにおいて;
志賀『位相への30講』第13講(pp.91-2):Rⁿにおいて;
神谷浦井『経済学のための数学入門』定理4.3.1(p.138) :n次元ユークリッド空間において;
杉浦『解析入門I』1章§4定理4.5-1(p.38):n次元ユークリッド空間において;
吹田新保『理工系の微分積分学』p.155-6　

※

活用例：点列のベクトル和の極限、点列と数列のスカラー積の極限　

※

ユークリッド距離と位相的に同値である距離をRⁿに与えてつくった距離空間でどうなるか
　　→矢野『距離空間と位相構造』例1.9(p.12)　　

→[トピック一覧：Rⁿにおける点列]
→総目次

定義：「有界」な点列

　・点列{P_n}の各点と原点Ｏ(0,0)との距離が、nによらない一定の実数を超えないとき、
　　点列{P_n}は「有界」であるという。[　小平邦彦『解析入門I』p. 65]　
　・点列{P_n}の各点の各座標が有界なるとき、点列が有界であるという。　[高木貞二『解析概論』p.14.]

cf.有界, 空間Rⁿにおける「有界」な点集合

→[トピック一覧：Rⁿにおける点列]
→総目次