コーシーの剰余項の導出
関数f(x) が閉区間[a,b]で(n−1)階まで連続な導関数をもち、開区間(a,b)でn階微分可能とする。
f(b)=f (a)+ f ' (a) (b−a) + f '' (a) (b−a)2/2!+…+ f (n-1) (a) (b−a) n-1/(n-1)!+Rn 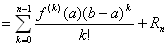
とおくと、
「Rn= f (n) (c) (b−c) n−1 (b−a) /( (n−1)! )」を満たすcが、開区間(a, b)内に存在する。
(つまり、「 Rn= f (n) (c) (b−c) n−1 (b−a) /( (n−1)! ) かつ a<c<b 」を満たすcが存在する)
ないしは、c を a +θ( b−a )と書いて(a<c<b ⇔ 0<θ<1 だから)
Rn= f (n) ( a +θ(b−a ) ) (b−a−θ(b−a )) n−1 (b−a) /( (n−1)! )
= f (n) ( a +θ(b−a ) ) ( (1−θ) (b−a )) n−1 (b−a) /( (n−1)! )
= f (n) ( a +θ(b−a ) ) (1−θ) n−1 (b−a)n /( (n−1)! )
を満たすθが開区間(0,1)内に存在する。
このRnを コーシーの剰余項 Cauchy form of the remainder と呼ぶ。
※ 以下のように書いても全く同じ。
f(b)=f (a)+ f ' (a) (b−a) + f '' (a) (b−a)2/2!+…+ f (n) (a) (b−a) n/n!+R n+1 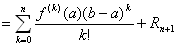
とおくと、
「 R n+1 = f (n+1)(c) (b−c)n (b−a) /n! 」を満たすcが、開区間(a, b)内に存在する。
ないしは、c を a + θ(b−a)と書いて、(a<c<b ⇔0<θ<1だから)
Rn+1 = f (n+1)( a +θ(b−a) ) (b−a−θ(b−a )) n (b−a) /(n!)
= f (n+1)( a +θ(b−a) ) ( (1−θ) (b−a )) n (b−a) /(n!)
= f (n+1)( a +θ(b−a) ) (1−θ)n (b−a)n+1 /(n!)
を満たすθが開区間(0,1)内に存在する。
※ f(n) の意味、 n!の意味、Σの意味
【解釈】
開区間(a, b)内のどこかに存在するcを用いると、f(b)をこのように「[n項までの級数]+[cを用いた剰余項]」で表せる!というのが、メインメッセージ。
【文献】
吹田・新保『理工系の…』p.46.]
(証明)
ポイント:ラグランジュ剰余項と異なった剰余項が導出される秘密は、[関数g(x)の設定]でのRnの係数の違いにある。
関数f(x) が閉区間[a,b]で(n−1)階まで連続な導関数をもち、開区間(a,b)でn階微分可能とする。
未知の定数Rnを用いて、
f(b)=f(a)+f ' (a) (b−a)+f '' (a) (b−a)2/2!+…+f (n-1) (a) (b−a)n-1/(n-1)!+Rn
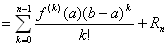 …(1)
…(1)
とおく。
(つまり、(1)が必ず成り立つように、未知の定数Rnを決めると考えればよい)
以下、この未知の定数Rnを求める。
[関数g(x)の設定]
以下のように、関数g(x)を、
ロールの定理が適用可能となるように、
すなわち、閉区間[a,b]で連続、開区間 (a,b)で微分可能、g(a)= g(b)となるように、
つくる。
Rnを定数として、
g (x)= f (x)+ f ' (x) (b−x)+f '' ( x ) (b−x)2/ (2! )+…+f (n−1) ( x ) (b−x )n-1/ ( (n-1) !)+Rn { (b−x ) / (b−a ) }
とする。 ((1)の右辺との違いはRnの係数だけ。)
(この係数こそが、ラグランジュ剰余項と違う剰余項を出すヒミツ。)
[ロールの定理の適用]
g (b)= f ( b )+ f ' ( b ) (b−b)+f '' ( b ) (b−b)2/ (2! )+…+f (n−1) ( b ) (b−b )n-1/ ( (n-1) !)+Rn { (b−b ) / (b−a ) }
=f ( b )+ f ' ( b ) 0 + f '' ( b ) 02 / (2! )+…+f (n−1) ( b ) 0n-1/ ( (n-1) !)+Rn { 0 / (b−a ) }
=f ( b )
g (a)= f ( a )+ f ' ( a ) (b− a)+f '' ( a ) (b−a)2/ (2! )+…+f (n−1) ( x ) (b−a)n-1/ ( (n-1) !)+Rn { (b−a ) / (b−a ) }
= f ( a )+ f ' ( a ) (b− a)+f '' ( a ) (b−a)2/ (2! )+…+f (n−1) ( x ) (b−a)n-1/ ( (n-1) !)+Rn} (これは(1)の右辺)
=f ( b ) ∵(1)
より、確かに、g(a)= g(b) = f(b)となる。
ロールの定理から、
g' (c) =0 をみたすcが、開区間(a, b)内に少なくとも一つ存在する、 … (2)
との結論を得る。
[g(x)の導関数]
g' (x)=f ' (x)+{ f ' (x) (b−x) }’+ (1/2! ) { f '' ( x ) (b−x)2 }’+…+(1/ (n-1)!){ f (n−1) ( x ) (b−x ) n-1 }’+{ Rn / (b−a ) } (b−x )’
∵和の微分、定数倍の微分
=f ' (x)+{ f '' ( x ) (b−x) +f ' (x) (b−x)’ }+ (1/2! ){ f ''' ( x ) (b−x ) 2+f '' ( x ) ( (b−x) 2)’}+…
…+(1/ (n-1)!) { f (n) ( x ) (b−x ) n-1 +f (n−1) ( x ) ( (b−x )n-1)’ }−{ Rn / (b−a ) }
∵積の微分
=f ' (x)+{ f '' ( x ) (b−x) +f ' (x) (−1) }+ (1/2! ){ f ''' ( x ) (b−x ) 2+f '' ( x ) ( −2(b−x))}+…
…+(1/ (n-1)!){ f (n) ( x ) (b−x ) n-1 +f (n−1) ( x ) (−(n-1) (b−x )n-2) }−{ Rn / (b−a ) }
∵合成関数の微分
=f ' (x)+{ f '' ( x ) (b−x) −f ' (x) }+{ (1/2! ) f ''' ( x ) (b−x ) 2+(−2/2! )f '' ( x ) (b−x) }+…
…+{ (1/ (n-1)!)f (n) ( x ) (b−x ) n-1 +(−(n-1)/ (n-1)!)f (n−1) ( x ) (b−x )n-2 }−{ Rn / (b−a ) }
=f ' (x)+{ f '' ( x ) (b−x) −f ' (x) }+{ f ''' ( x ) (b−x ) 2/ (2!)−f '' ( x ) (b−x) }+…
…+{ f (n) ( x ) (b−x ) n-1/( (n-1)!)−f (n−1) ( x ) (b−x )n-2/( (n-2)!) }−{ Rn / (b−a ) }
∵ 係数を約分しただけ
=f ' (x)+{ −f ' (x) + f '' ( x ) (b−x)}+{−f '' ( x ) (b−x)+ f ''' ( x ) (b−x ) 2/ (2! ) }+…
…+{ −f (n−1) ( x ) (b−x )n-2/( (n-2)!) + f (n) ( x ) (b−x ) n-1/( (n-1)!)}−{ Rn / (b−a ) }
∵ { }内の足し算の順番を入替ただけ
=f (n) ( x ) (b−x ) n-1/( (n-1)!)−{ Rn / (b−a ) }
∵ { }を越えて隣りあう項が打ち消しあって残るのはこの2項。
(2)より
g' (c)=f (n) ( c ) (b−c ) n-1/( (n-1)!)−{ Rn / (b−a ) }=0 (※)
をみたすcが、開区間(a,b)内に少なくとも一つ存在する。
(※)はすなわち、
{ Rn / (b−a ) }=f (n) ( c ) (b−c ) n-1/( (n-1)!)
Rn =f (n) ( c ) (b−c ) n-1(b−a ) /( (n-1)!) …(3)
ゆえに、(3)をみたすcが、開区間(a,b)内に少なくとも一つ存在する、ということになる。