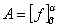実2次元数ベクトル空間R2上の一次変換の行列表示と標準化　　―　　トピック一覧　
・定理：標準基底に関する一次変換の行列表現/一次変換の行列と基本ベクトルのうつしかたの関連　
・定理：任意の基底に関する一次変換の行列表現/一次変換の行列表示の標準形は得られない/一次変換の合成写像と行列
※関連ページ：
　・R2上の一次変換と行列の関係について：R2上の一次変換の定義/基底変換と一次変換の行列表示/　　
　・一般化：一次写像「f:Rn→Rm」の行列表示と標準化/一般の実ベクトル空間のあいだの一次写像の行列表示と標準化/基底の変換と一次写像と行列　
※線形代数目次・総目次


定理：実2次元数ベクトル空間上の一次変換の、標準基底に関する行列表示

[設定]
この定理は、以下の舞台設定上で成り立つ。
R：実数体(実数をすべて集めた集合）　　　　
R2：実2次元数ベクトル空間。　
　　すなわち、R2＝R×R＝{ ( x,y )｜x∈Rかつy∈R }に、
　　　　　　　　ベクトルの加法とスカラー乗法を定義したもの。　
　　ただし、R2に属すすべての実2次元数ベクトルは、
             2次元縦ベクトルの形式で表されているものとする。
f　：2変数2値ベクトル値関数。

[文献－線型代数]
・志賀『線形代数30講』6講(pp.37-8);7講(pp.42-5):R2上の一次変換のケース;10講(p.63);
・佐武『線形代数学』Ⅰ§4(p.20)

[文献－解析学/数理経済]
・松坂『解析入門4』15.1-E命題11(p.10);F注(p.13); 18.1-A (pp.84-5);標準基底に関する表現行列
・神谷浦井『経済学のための数学入門』§5.2.1例5.2.1(p.165)　
・戸田山田『計量経済学の基礎：統計的手法の理論とプログラミング』2.5.1(pp.84-5)
[本論1] 以下の命題Pと、命題Q1～Q4は、同値。
つまり、
　　命題P⇔命題Q1⇔命題Q2⇔命題Q3⇔命題Q4

命題P ： 2変数2値ベクトル値関数　(x',y')＝f(x,y)　　　
あるいは、実2次元ベクトルを縦に書いた　　
 ( x' ) =　f　
 ( x )
y' y
　　　　　 は、「R2上の一次変換」の定義を満たす。






[P⇒Qの証明]　　[文献]志賀『線形代数30講』7講(p.43);戸田山田『計量経済学の基礎』2.5.1(p.84)
準備1:任意の(x,y)∈R2　は、(x,y)＝x(1,0)+y(0,1)　と表せる。(∵)
準備2:2変数2値ベクトル値関数fによる像は、
　　　どれも、実2次元数ベクトル。
　　　そこで、
      《fによる(1,0)の像》f(1,0) を、　( a11,a21)　とおく。　　　
　　　《fによる(0,1)の像》f(0,1) を、　( a12,a22)　とおく。
　　　なお、2変数2値ベクトル値関数は、写像の下位類型であり、
　　　また、写像は「定義域の元に対応する値は必ず一つ」と定義されたので、
　　　　　ここのf(1,0)=( a11,a21), f(0,1)=( a12,a22)　も、一意的である。　　　
本題: 命題P「2変数2値ベクトル値関数fは『R2上の一次変換』の定義を満たす」のもとで、
　　　以下が成り立つ。
　　　任意の(x,y)∈R2　について、
　　　　　f(x,y)＝f( x(1,0)+y(0,1) )　　　　　∵準備1
　　　　　　　　＝f( x(1,0) )　+　f( y(0,1) )　∵命題Pのもとで、fは一次変換の要件1を満たす。
　　　　　　　　＝xf( (1,0) )　+　yf( (0,1) )　∵命題Pのもとで、fは一次変換の要件2を満たす。
　　　　　　　　＝x( a11,a21)　+　y( a12,a22)　　∵準備2。( a11,a21),( a12,a22)の一意性に注意。
　　　　　　　　＝( a11x,a21x)+( a12y,a22y)　∵実2次元数ベクトル空間に定義されたスカラー乗法
　　　　　　　　＝( a11x + a12y , a21x + a22y )　∵実2次元数ベクトル空間に定義されたベクトル和
　　　これは、命題Q1に他ならない。

[Q⇒Pの証明]　[文献] 志賀『線形代数30講』6講(p.38);戸田山田『計量経済学の基礎』2.5.1(pp.84-5)　
　命題Q1が成り立ち、
　　2変数2値ベクトル値関数f(x,y) に対して、実数a11 ,a12 ,a21 ,a22 が一意的に存在し、
　　　f(x,y)＝( a11x＋a12y , a21x＋a22y )
　　と表されるとする。
　　すると、
　 ・任意の(xu,yu),(xv,yv)∈R2　　について、
　　　f(xu,yu)+ f(xv,yv)＝( a11xu＋a12yu,a21xu＋a22yu ) + ( a11xv＋a12yv,a21xv＋a22yv ) 　∵命題Q1
  　　　　　　　　　　　＝( a11xu＋a12yu＋a11xv＋a12yv ,  a21xu＋a22yu ＋a21xv＋a22yv )　
　　　　　　　　　　　　　　　　　　　　　　　　　　∵実2次元数ベクトル空間に定義されたベクトル和　
  　　　　　　　　　　　＝( a11(xu＋xv)＋a12(yu＋yv) ,  a21(xu＋xv)＋a22(yu＋yv) )　∵実数体の分配則
　　　　　　　　　　　　＝f( (xu＋xv),(yu＋yv) )　　　　　　　　　　∵命題Q1　　　　　　　　　　
　　・任意のa∈R,(x,y)∈R2　について、
　　　　　　　　af(x,y)＝a( a11x＋a12y , a21x＋a22y )　　　∵命題Q1
　　　　　　　　　　　　＝(  a(a11x＋a12y), a(a21x＋a22y) )　∵実2次元数ベクトル空間に定義されたスカラー倍　
　　　　　　　　　　　　＝(  a11ax＋a12ay, a21ax＋a22ay )　　∵実数体の分配則　
　　　　　　　　　　　　＝f(ax,ay)　　　　　　　　　　　　∵命題Q1　
　　が成り立つ。
　　この二点は一次変換の要件1,2に他ならないので、
　　命題Q1が成り立つならば、
　　命題P「2変数2値ベクトル値関数fは『R2上の一次変換』の定義を満たす」が成り立つ。

命題Q1： 2変数2値ベクトル値関数　(x',y')＝f(x,y) に対して、
　　　　　実数a11 ,a12 ,a21 ,a22 が一意的に存在し、
　　　　　(x',y')＝f(x,y) は、実数a11 ,a12 ,a21 ,a22 を用いた次式で表される。　
　　　　　　　　　　　(x',y')＝f(x,y) ＝( a11x＋a12y , a21x＋a22y )

命題Q2： 2変数2値ベクトル値関数　(x',y')＝f(x,y) に対して、
　　　　　実数a11 ,a12 ,a21 ,a22 が一意的に存在し、
　　　　　　2変数2値ベクトル値関数　(x',y')＝f(x,y) 　を、
　　　　　　　x'＝f1(x,y) 　
　　　　　　　y'＝f2(x,y) 　
　　　　　　という2 変数関数f1,f2の 組として表すとき、
　　　　　　これらの2 変数関数は、実数a11 ,a12 ,a21 ,a22 を用いて、
　　　　　　　　　x'＝f1(x,y) ＝a11x＋a12y　
　　　　　　　　　y'＝f2(x,y) ＝ a21x＋a22y 　
　　　　　　と表される。

命題Q3：
2変数2値ベクトル値関数　　
 ( x' ) =　f　
 ( x )
y' y
　　　　　に対して、　　　　
2次正方行列　
 A＝
 ( a11
 a12
 )
a21
 a22
　　　　　が一意的に存在し、
　　　　　　　 f　は、Aの 行列積を用いて、

 ( x' )
 		=　 f
(
 		x )
 ＝
 ( a11 a12 )(
 		x )
 		  

y' y a21 a22 y
  
　　　　と表される。　
　　　　　（この行列積を 計算してみると、命題Q3は命題Q1,Q2に一致する。）
命題Q4：v,wを実2次元縦ベクトル、f を2変数2値ベクトル値関数とする。
　　　　2変数2値ベクトル値関数　w＝ f (v)　に対して、
　　　　　2次正方行列Aが 一意的に存在して、　　　　　　　
　　　　　2変数2値ベクトル値関数w＝f(v) 　は、2次正方行列Aを 用いて、
　　　　　　　　w＝f(v) ＝Av　
　　　　　　と表される。
　　　　　　　*Aは2次正方 行列、vは実2次 元縦ベクトル(つまり、(2,1)型 実行列)だから、
　　　　　　　　行列積の 定義により、(Av)は、
　　　　　　　　　実2次元数ベクトル(つま り、(2,1)型実行列)となる。


[本論2]
すると、
任意の2次正方行列Aに対して、 「f(v) ＝Av」 で定義される一次変換fが 一意的に存在し、
また逆に、
任意の一次変換fに対 して、(∀v∈R2) ( f(v)=(Av) )を満たす2次正方行列Aが 一意的に存在する
ことになる。
つまり、
(∀v∈R2) ( f(v)=(Av) )　という関係によって、
2次正方行列Aを一つ 決めれば、一次変換fを 一意的に定められ、
一次変換fを 一つ決めれば、2次正方行列Aを 一意的に定められる、
という、
一意的な対応関係が、2次正方行列と一次変換とのあいだには存在す る。

[本論3] ・上記の2次正方行列Aを、
　　「一次変換fに対応する行列」、「一次変換fの行列」、
　厳密には、
　　「R2の標準基底{ e1, e2 }に関する一次変換fの表現行列」
　と呼ぶ。
・上記の一次変換fを、
　　「Aによって定義される一次変換」
　と呼ぶ。
・「R2の標準基底{ e1, e2}に関する一次変換fの表現行列」が、
　任意基底に関する一次変換fの表現行列と、
　いかなる関係にあるかは、
　基底変換公式を見よ。　　
 [関連項目]
※一般化―　基底の一般化：
　・任意基底に関する一次変換f:R2→R2の行列表示　
※一般化―　R2の一般化：
　・標準基底に関する一次変換f:Rn→Rnの行列表示　　　　
　・標準基底に関する一次写像f:Rn→Rmの行列表示　
※発展事項：一次変換の行列表示の標準形/基底変換の行列　　
図解
[図解：2次正方行列によって定義される一次変換の挙動]
2次正方行列
( )
によって定義される一次変換fの 挙動は、x-y平面上、以下のように図示できる。
図中の「矢印の終点」が、「一次変 換fによって『矢印の始点』をうつした像」と なっている。

R2上の一次変換の挙動の図示


→[トピック一覧：実2次元数ベクトル空間R2上の一次変換の表現行列]
→線形代数目次・総目次

　
定理：行列によって定義される一次変換は、基本ベクトルをどのように写すか

設定
この定理は、以下の舞台設定上で成り立つ。
R：実数体(実数をすべて集めた集合）　　
A：2次正方行列　
R2：実2次元数ベクトル空間。　
　　すなわち、R2＝R×R＝{ ( v1, v2 )｜v1∈Rかつv2∈R }に、
　　　　　　　　ベクトルの加法とスカラー乗法を定義したもの。　
　　ただし、R2に属すすべての実2次元数ベクトルは、
　　　　　　　　2次元縦ベクトルの形式で表されているものとする。
v：実2次元縦ベクトル
 [文献－線型代数]
・永田『理系のための線形代数の基礎』1.4行列と一次写像:注意1(p.29);
・志賀『線形代数30講』7講:R2上の一次変換のケース(p.44)

[文献－解析学]
・松坂『解析入門4』15.1-E命題11 (p.10)
本論 2次正方行列
　
 A＝
 ( a11
 a12
 )
a21
 a22
によって定義された一次変換を、f:R2→R2で 表すと、　　
R2の基本ベクトルe1, e2のfに よる像 f(e1) , f(e2)  ∈R2は、
　　

 f(e1)=
 ( a11
 )
a21



f(e2)=
 ( a12
 )
a22

となる。
　
証明 ※なぜ？→行列と基本ベクトルとの積。
　

→[トピック一覧：実2次元数ベクトル空間R2上の一次変換の表現行列]
→線形代数目次・総目次


　
定理：任意の基底に関する一次変換の行列表示･行列表現

設定
この定理は、以下の舞台設定上で成り立つ。
R：実数体(実数をすべて集めた集合）　　
R2：実2次元数ベクトル空間。　
　　すなわち、R2＝R×R＝{ ( v1, v2 )｜v1∈Rかつv2∈R }に、
　　　　　　　　ベクトルの加法とスカラー乗法を定義したもの。　
　　ただし、R2に属すすべての実2次元数ベクトルは、
　　　　　　　　2次元縦ベクトルの形式で表されているものとする。
{ p1, p2 }：R2の基底をなす実2次元数ベクトルの集合
[文献]
・松坂『解析入門4』15.1-E命題11(p.10);F注(p.13); 18.1-A (pp.84-5);
・神谷浦井『経済学のための数学入門』§5.2.1例5.2.1(p.165)　

[関連項目]
※具体化：
　・標準基底に関する一次変換f:R2→R2の行列表示
※一般化：
　・任意基底に関する一次変換f:Rn→Rnの行列表示　
　・任意基底に関する一次写像f:Rn→Rmの行列表示
※発展事項：
　・一次変換の行列表示の標準形
　・基底変換の行列
　・基底変換公式
本論1 R2の基底{ p1, p2 }と、一次変換「f:R2→R2」にたいして、　
　　f(p1)=a11 p1＋a21 p2
　　f(p2)=a12 p1＋a22 p2
を満たす2次正方行列 　
　
 A＝
 ( a11
 a12
 )
a21
 a22
が一意的に存在する。　　

本論2 R2の基底{ p1, p2 }と、
2次正方行列 　
　
 A＝
 ( a11
 a12
 )
a21
 a22
にたいして、
　　f(p1)=a11 p1＋a21 p2
　　f(p2)=a12 p1＋a22 p2 　　　　
を満たす一次変換「f:R2→R2」がきまる。　　　
　　　
証明 ※なぜ？→証明

本論3 ・上記の2次正方行列Aを、　
　　基底{ p1, p2 }に関する一次変換fの行列表示、　　
　　基底{ p1, p2 }に関する一次変換fの表現行列、　　
　　基底{ p1, p2 }を定めたとき一次変換fに対応する行列　　
　などと呼ぶ。
・基底{ p1, p2 }に関する一次変換fの表現行列が、
　標準基底に関する一次変換fの表現行列と、
　いかなる関係にあるかは、
　基底変換公式を見よ。
　
※発展事項：一次変換の行列表示の標準化の問題/基底変換の行列/基底変換公式　
　

※

 要するに、

「『Rnの基底』α={ p1, p2, …, pn }, 『Rmの基底』β={q1, q2, …, qm}に関する一次写像『f: Rn→Rm』の表現行列」
　　　
のうち、
　　[条件1]　n=m=2であること、
　　[条件2] 『Rmの基底』β={ q1, q2, …, qm }が、α={ p1, p2, …, pn  }であること
を満たす特殊例が、
「基底{ p1, p2 }に関する『一次変換f: R2→R2』の表現行列」
に他ならない。　　

本論4 [一次変換y=f (x)の行列表現]
・実2次元数ベクトル空間 R2 に属す任意の実2次元数ベクトルxは、
　『R2の基底』α={ p1, p2 }の一次結合として一意的に表せる（∵基底の定義）。
　したがって、
　　任意のx∈R2に対して、ある実数x1,x2 が一意に存在して、
　　　　x＝x1p1＋x2p2　
　　を満たす。
　この実数の組(x1,x2) の縦ベクトルを、
　　xの《R2の基底α={ p1, p2 }》に関する座標ベクトルと呼び、
 　　　[x]α　
　　と表す。
　　また、
　　任意のy∈Rnに対しても、ある実数y1,y2が一意に存在して、
　　　　y＝y1p1＋y2p2　
　　を満たす。
　この実数の組(y1,y2)の縦ベクトルを、
　　yの《R2の基底α={ p1, p2 }》に関する座標ベクトルと呼び、
　　　[y]α　
　　と表す。
・すると、一次変換y=f (x)は、
　　　xの《R2の基底α={ p1, p2 }》に関する座標ベクトル [x]α　
　　　yの《R2の基底α={ p1, p2 }》に関する座標ベクトル[y]α　
 　　　《R2の基底α={ p1, p2 }》に関する一次変換fの表現行列A
　を用いて、
　　[y]α＝A[x]α　
　と表せる。
[文献]
・斎藤『線形代数入門』4章§5(p.117);

→[トピック一覧：実2次元数ベクトル空間R2上の一次変換の表現行列]
→線形代数目次・総目次




定理：一次変換の行列表示の標準形は得られない

設定
この定理は、以下の舞台設定上で成り立つ。
R：実数体(実数をすべて集めた集合）　　
R2：実2次元数ベクトル空間。　
　　すなわち、R2＝R×R＝{ ( v1, v2 )｜v1∈Rかつv2∈R }に、
　　　　　　　　ベクトルの加法とスカラー乗法を定義したもの。　
　　ただし、R2に属すすべての実2次元数ベクトルは、
　　　　　　　　2次元縦ベクトルの形式で表されているものとする。
「f:R2→R2」：一次変換　
rank f ：一次変換 f の階数
 [文献－線型代数]
・志賀『線形代数30講』26講(pp.166-167);
・斎藤『線形代数入門』４章§5 (p.117);
本論1 「任意の一次変換『f:R2→R2』には、
　　　・rank f ＝2 ならば、『f(p1)＝ p1 かつ f(p2)＝ p2』を満たす『R2の基底』{ p1, p2 }  が存在する
　　　・rank f ＝1 ならば、『f(p1)＝ p1 かつ f(p2)＝０』を満たす『R2の基底』{ p1, p2 }  が存在する」
とはいえない。
・確かに、2次単位行列によって定義された一次変換のように、
　　　　　『f(e1)＝ e1 かつ f(e2)＝ e2』を満たす『R2の基底』{ e1,  e2 }  を有す一次変換もある。
・しかし、「どの一次変換『f:R2→R2』でも、このような条件を満たす基底を有す」とはいえない。　
証明 　[反例を示す]
本論2 したがって、
「任意の一次変換『f:R2→R2』にたいして、
　　　ある『R2の基底』{ p1, p2 } をとると、
　　　　これらの基底に関する一次変換fの行列表示を、

　　　　　・rank f ＝2 ならば、

 D(2,2,2)=
 ( 1
 0
 )
0
 1
　　　　　・rank f ＝1 ならば、

 D(2,2,1)=
 ( 1
 0
 )
0
 0
　とできる」
とはいえない。

Cf　
※ここで利用されている事項：基底に関する一次変換fの行列表示　

※一次写像一般では、一次写像の行列表示の標準形が得られるのに、
　なぜ、ここで、一次変換の行列表示の標準形が得られなくなるのか？
　[・志賀『線形代数30講』20講Teatime(p.131);26講(pp.164-167);
　　　斎藤『線形代数入門』４章§5 (p.117);]

　
　 　
・確かに、2次単位行列によって定義された一次変換のように、
　　　『R2の基底』{ e1,  e2 } をとると、
　　　この基底に関する一次変換fの行列表示を、

D(2,2,2)＝
 ( 1
 0
 )
0
 1
　　　とできる一次変換もある。
・しかし、「どの一次変換『f:R2→R2』でも、このような条件を満たす基底を有す」とはいえない。
　
本論3 「R2の標準基底{ e1, e2}に関する一次変換fの行列表示」Aにたいして、
ある実行列Pが存在し、


　　　　　・rank f ＝2 ならば、

 P-1AP = D(2,2,2)＝
 ( 1
 0
 )
0
 1
　　　　　・rank f ＝1 ならば、


 P-1AP = D(2,2,1)＝
 ( 1
 0
 )
0
 0

　とできる」
を満たす
とはいえない。
 ※一次変換の行列表示のケースとの違い：　
※ここで利用されている事項：
　　　基底に関する一次変換fの行列表示/基底変換の行列/基底変換公式　
　
証明 　
本論4

ところが、
ある種の一次変換『f:R2→R2』には、
　　　f (p1)=λ1 p1, f (p2)=λ2 p2　（λ1,λ2はfの固有値）
を満たす『R2の基底』{ p1, p2 }が存在する。

したがって、
ある種の一次変換『f:R2→R2』に対して、
ある『R2の基底』{ p1, p2 }をとると、
これらの基底に関する一次変換fの行列表示は、

 diag(λ1,λ2)=
 ( λ1 0
 )
0
 λ2

となる。
だから、
ある種の一次変換『f:R2→R2』については、
「R2の標準基底{ e1, e2} に関する一次変換fの行列表示Aにたいして、
ある実行列Pが存在し、
　P－１AP=diag(λ1,λ2)　
を満たす。
 そこで、一次変換では、
標準化にかわって、このようなかたちに変形することが課題として浮上する。
一次変換の行列表示を、このようなかたちにできることを対角化可能といい、
一次変換の行列表示が対角化可能となる条件を求める問題は、固有値問題と呼ばれる。
 　
証明 　

→[トピック一覧：実2次元数ベクトル空間R2上の一次変換の表現行列]
→線形代数目次・総目次

　
定理：実行列との乗法による一次写像の合成写像

設定
この定理は、以下の舞台設定上で成り立つ。
R：実数体(実数をすべて集めた集合）　　
A：2次正方行列　
B：2次正方行列　
v：実2次元縦ベクトル
R2：実2次元数ベクトル空間。　
　　すなわち、R2＝R×R＝{ ( v1, v2 )｜v1∈Rかつv2∈R }に、
　　　　　　　　ベクトルの加法とスカラー乗法を定義したもの。　
　　ただし、R2に属すすべての実2次元数ベクトルは、
　　　　　　　　2次元縦ベクトルの形式で表されているものとする。
「A：R2→R2」：2次正方行列Aと実2次元縦ベクトルとの乗法による
　　　　　　　　　実2次元数ベクトル空間R2上の一次変換　
「B：R2→R2」：2次正方行列Bと実2次元縦ベクトルとの乗法による
　　　　　　　　　実2次元数ベクトル空間R2上の一次変換


[文献－線型代数]
　永田『理系のための線形代数の基礎』(p.26-7);
　斎藤『線形代数入門』2章§3(p.45);
　佐武『線形代数学』Ⅰ§4(p.20)
[文献－解析学]
　松坂『解析入門4』15.1-E命題12 (p.11);
本論 一次変換A：R2→R2と、一次変換B：R2→R2　の合成写像B〇Aは、　　
行列積BA[2次正方行列]と実2次元縦ベクトルとの乗法で表せる。
　
解説 なぜなら、
合成写像B〇Aとは、
実2次元縦ベクトル   v＝
 ( v1
 )
v2

 　に対して、
　　B(Av)　
とすること。
ところが、結合則より、
　　B(Av)=(BA)v　
　

→[トピック一覧：実2次元数ベクトル空間R2上の一次変換の表現行列]
→線形代数目次・総目次

(reference)
日本数学会編集『岩波数学辞典（第三版）』 岩波書店、1985年、項目83行列L線形写像(p.222)
線形代数のテキスト
志賀浩二『数学30講シリーズ：線形代数30講』朝倉書店、1988年、7講線形写像と行列(pp.42-7)、10講R3上の線形写像(pp.62-7)、17講線形写像(pp.107-112)。
ホフマン・クンツェ『線形代数学I』培風館、1976年、3.4行列による一次変換の表現(p.89)。
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、1.4行列と一次写像(pp.23-31)。
藤原毅夫『理工系の基礎数学2：線形代数』岩波書店、1996年、4.3線形写像の階数と行列の階数(p.102)。
斎藤正彦『線形代数入門』東京大学出版会、1966年、第2章§3行列と線形写像(pp.44-5):実線形空間･複素線形空間のみ;。
佐武一郎『線形代数学(第44版)』裳華房、1987年、Ⅰベクトルと行列の演算§4一次写像(pp.17-19)。
代数学のテキスト
酒井文雄『共立講座21世紀の数学8：環と体の理論』共立出版、1997年、1.6ベクトル空間(p.22)。:数ページしか触れていないが、逆に、一般の線形空間の理論の骨組みだけを浮かびあがってくるので、何が重要事項なのかを見極める上で便利。
数理経済学のテキスト
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、§5.2.1線形写像の行列表現(p.165)。
→[トピック一覧：実2次元数ベクトル空間R2上の一次変換の表現行列]
→線形代数目次・総目次