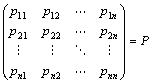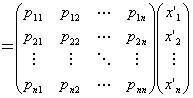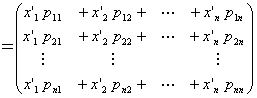実n次元数ベクトル空間Rnの基底変換と、一次写像「f:Rn→Rm」の行列表現についての基底変換公式
　・定義：基底変換行列/相似/変換する　　
　・定理：基底変換行列は正則/基底変換行列の逆行列
　・定理：一次写像の行列表示に関する基底変換公式/一次変換の行列表示に関する基底変換公式　
※関連ページ：
・一次写像「f:Rn→Rm」と行列の関係について：実n次元数ベクトル空間から実m次元数ベクトル空間への一次写像/一次写像f:Rn→Rmの行列表示と標準化/　　
・実ベクトル空間のあいだの一次写像と行列の関係について：実ベクトル空間のあいだの一次写像/一般の実ベクトル空間のあいだの一次写像の行列表示と標準化/基底変換と一次写像と行列　
※線形代数目次・総目次・文献一覧
定義：実n次元数ベクトル空間の基底変換行列

設定
この定理は、以下の舞台設定上で成り立つ。
R：実数体(実数をすべて集めた集合）　　
Rn：実n次元数ベクトル空間。　
　　すなわち、Rn＝R×R×…×R＝{ ( v1, v2, …, vn )｜v1∈Rかつv2∈Rかつ…かつvn∈R }に、
　　　　　　　　ベクトルの加法とスカラー乗法を定義したもの。　
　　ただし、Rnに属すすべての実n次元数ベクトルは、n次元縦ベクトルの形式で表されているものとする。
x：実n次元縦ベクトル　t( x1,x2,…,xn )∈ Rn
p1：実n次元縦ベクトル　t( p11,p21,…,pn1 )∈ Rn
p2：実n次元縦ベクトル　t( p12,p22,…,pn2 )∈ Rn
:
pn：実n次元縦ベクトル　t( p1n,p2n,…,pnn )∈ Rn
[文献]
・松坂『解析入門4』18.1-A命題1 (p.85)
※一般化：実ベクトル空間一般の基底変換行列　
※関連事項：正則行列と基底変換行列とのリンク、直交行列と基底変換行列とのリンク　
本題1 「『Rnの標準基底{ e1, e2, …, en }』から『Rnの基底{ p1, p2, …, pn }』への基底変換行列」
「『基底の変換{ e1, e2, …, en }→{ p1, p2, …, pn }』の行列」
とは、
実n次正方行列であって、
その第1列がp1, その第2列がp2, …, その第n列がpnとなるもの
　　
のことをいう。　　
本論2 [《任意基底に関する座標ベクトル》から《標準基底に関する座標ベクトル》への変換]
・実n次元数ベクトル空間Rn に属す任意の実n次元縦ベクトルx=t( x1,x2,…,xn )は、
　　Rnの基底{ p1, p2, …, pn }の一次結合として一意的に表せる（∵基底の定義）。
　つまり、
　　任意のx∈Rnに対して、ある実数 x'1,x'2,…,x'n が一意に存在して、
　　　　x ＝ x'1 p1 + x'2 p2 +…+ x'n pn　…(1)
　　を満たす。
　この実数の組(x'1,x'2,…,x'n )の縦ベクトルを、
　　xの《Rnの基底{ p1, p2, …, pn } 》に関する座標ベクトルと呼び、
　　　x'　
　　と表す。
 ・すると、
　「xの《Rnの基底{ p1, p2, …, pn } 》に関する座標ベクトルx'＝t( x'1,x'2,…,x'n )  の左から、
 　「標準基底{ e1, e2, …, en }から基底{ p1, p2, …, pn }への基底変換行列」P
　を掛けると、
　実n次元縦ベクトルx=t( x1,x2,…,xn )
　に戻る。
　つまり、
　　　Px'＝x　
　が成り立つ。　
　実際、
　　Px'　
　　　
　　　
　　＝ x'1 p1 + x'2 p2 +…+ x'n pn　
　　＝ x　　　∵(1)　
 [amazon:tate-big:jp]
　 　
本論3 ・基本ベクトルe1, e2, …, enの左から「標準基底{ e1, e2, …, en }から基底{ p1, p2, …, pn}への基底変換行列」Pをかけると、
　基底変換行列の定義と行列積の計算から、　　
　　Pe1= p1　　　　
　　Pe2= p2　
　　　：：　
　　Pen= pn　　
　となる。
 ・この単なる行列積の計算を、基底変換の文脈でとらえかえすと…。
　　(1)
　　基本ベクトルe1＝t( 1 ,０,…,０)とは、「p1の《Rnの基底 {  p1, p2, …, pn } 》に関する座標ベクトル」である。
 　　　実際、 p1= 1p1 + ０p2 +…+ ０pn　。
　　一般に、
　　「xの《Rnの基底 { p1, p2, …, pn } 》に関する座標ベクトルx'=t ( x'1 , x'2 ,…, x'n ) 」の左から、
　　「標準基底{ e1, e2, …, en }から基底{ p1, p2, …, pn }への基底変換行列」P
　　を掛けると、
　　標準基底に関する座標ベクトルx=t ( x1 , x2 ,…, xn )　
　　に戻る。
　　したがって、
　　「p1の《Rnの基底 { p1, p2, …, pn } 》に関する座標ベクトル」e1=t ( 1 ,０,…,０)の左から、
　　「標準基底{ e1, e2, …, en }から基底{ p1, p2, …, pn }への基底変換行列」P
　　を掛けると、
　　標準基底に関する座標ベクトルp1=t( p11, p21, …, pn1 )　
　　に戻る。
　　だから、Pe1= p1　　　　
　　(2)
　　基本ベクトルe2=t (０, 1,０,…,０)とは、「p2の《Rnの基底 { p1, p2, …, pn } 》に関する座標ベクトル」である。
　　　実際、p1=０p1 + 1p2 +０p3 +…+ ０pn　。　　
　　一般に、
　　「xの《Rnの基底 { p1, p2, …, pn } 》に関する座標ベクトルx'=t ( x'1 , x'2 ,…, x'n ) 」の左から、
　　「標準基底{ e1, e2, …, en }から基底{ p1, p2, …, pn }への基底変換行列」P
　　を掛けると、
　　標準基底に関する座標ベクトルx=t ( x1 , x2 ,…, xn )　
　　に戻る。
　　したがって、
　　「p2の《Rnの基底 { p1, p2, …, pn } 》に関する座標ベクトル」e2=t (０, 1,０,…,０)の左から、
　　「標準基底{ e1, e2, …, en }から基底{ p1, p2, …, pn }への基底変換行列」P
　　を掛けると、
　　標準基底に関する座標ベクトルp2=t( p12, p22, …, pn2 )　
　　に戻る。
　　だから、Pe2= p2
　　：
　　：
　　(n)
　　基本ベクトルen =t(０,…,０,１)とは、「p nの《Rnの基底 { p1, p2, …, pn } 》に関する座標ベクトル」である。
　　　実際、p1=０p1 +…+０pn－1 + 1pn　。　　
　　一般に、
　　「xの《Rnの基底 { p1, p2, …, pn } 》に関する座標ベクトルx'=t ( x'1 , x'2 ,…, x'n ) 」の左から、
　　「標準基底{ e1, e2, …, en }から基底{ p1, p2, …, pn }への基底変換行列」P
　　を掛けると、
　　標準基底に関する座標ベクトルx=t ( x1 , x2 ,…, xn )　
　　に戻る。
　　したがって、
　　「p nの《Rnの基底 { p1, p2, …, pn } 》に関する座標ベクトル」en =t (０,…,０,１)の左から、
　　「標準基底{ e1, e2, …, en }から基底{ p1, p2, …, pn }への基底変換行列」P
　　を掛けると、
　　標準基底に関する座標ベクトルpn =t( p1n, p2n, …, pnn )　
　　に戻る。
　　だから、Pen= pn　　　　
　　　　　　　
　 　
　
→[トピック一覧：基底変換と一次写像]
→線形代数目次・総目次
　
定理：基底変換の行列は正則行列

設定
この定理は、以下の舞台設定上で成り立つ。
R：実数体(実数をすべて集めた集合）　　
Rn：実n次元数ベクトル空間。　
　　すなわち、Rn＝R×R×…×R＝{ ( v1, v2, …, vn )｜v1∈Rかつv2∈Rかつ…かつvn∈R }に、
　　　　　　　　ベクトルの加法とスカラー乗法を定義したもの。　
　　ただし、Rnに属すすべての実n次元数ベクトルは、n次元縦ベクトルの形式で表されているものとする。
x：実n次元縦ベクトル　t( x1,x2,…,xn )∈ Rn
{ e1, e2, …, en }：「Rnの標準基底」
{ p1, p2, …, pn }：「Rnの基底」の一つ。　
[文献]
・松坂『解析入門4』18.1-A (p.84)
本題 標準基底{ e1, e2, …, en }から基底{ p1, p2, …, pn }への基底変換行列は、
正則行列。
証明 ・「標準基底{ e1, e2, …, en }から基底{ p1, p2, …, pn }への基底変換行列」とは、
　　その第1列をp1, その第2列をp2, …, その第n列をpnとする実n次正方行列であった。　
・実n次元数ベクトル空間Rnの基底をなすための必要十分条件より、
　「n個の実n次元数ベクトルp1, p2, …, pnが、『Rnの基底』をなす」と「n個の実n次元数ベクトルp1, p2,…, pnが、一次独立」とは同値。
　したがって、「標準基底{ e1, e2, …, en }から基底{ p1, p2, …, pn }への基底変換行列」の各列は、ベクトルとして一次独立である。
・正則行列になるための必要十分条件より、「行列Pの各列がベクトルとして一次独立」⇔「行列Pが正則行列」。
　したがって、「標準基底{ e1, e2, …, en }から基底{ p1, p2, …, pn }への基底変換行列」は、正則行列である。　　　　


→[トピック一覧：基底変換と一次写像]
→線形代数目次・総目次		 　
　
定理：実n次元数ベクトル空間から実m次元数ベクトル空間への一次写像の行列表示に関する基底変換公式


設定


この定理は、以下の舞台設定上で成り立つ。
R：実数体(実数をすべて集めた集合）　　
A：(m,n)型実行列　
Rn：実n次元数ベクトル空間。　
　　すなわち、Rn=R×R×…×R＝{ ( v1, v2, …, vn )｜v1∈Rかつv2∈Rかつ…かつvn∈R }に、
　　　　　　　　ベクトルの加法とスカラー乗法を定義したもの。　
　　ただし、Rnに属すすべての実n次元数ベクトルは、 n次元縦ベクトルの形式で表されているものとする。
　・{ e1, e2, …, en }：「Rnの標準基底」
　・{ p1, p2, …, pn }：「Rnの基底」の一つ。　
　・P：『Rnの基底』を、『Rnの標準基底』{ e1, e2, …, en }から{ p1, p2, …, pn }へ変えたときの基底変換行列
Rm：実m次元数ベクトル空間。　
　　すなわち、Rm=R×R×…×R＝{ ( v1, v2, …, vm )｜v1∈Rかつv2∈Rかつ…かつvm∈R }に、
　　　　　　　　ベクトルの加法とスカラー乗法を定義したもの。　　　　　
　　ただし、Rmに属すすべての実m次元数ベクトルは、 m次元縦ベクトルの形式で表されているものとする。
　・{ e'1, e'2, …, e'm }：「Rmの標準基底」　　
　・{ q1, q2, …, qm }：「Rmの基底」の一つ。　　
　・Q：『Rmの基底』を、『R mの標準基底』{ e'1, e'2, …, e'm }から{ q1, q2, …, qm }へ変えたときの基底変換行列　
「f : Rn→Rm」：RnからRmへの一次写像　
A：『Rnの標準基底』{ e1, e2, …, en },『R mの標準基底』{ e'1, e'2, …, e'm }に関する一次写像fの行列表示　
B：『Rnの基底』{ p1, p2, …, pn },『Rmの基底』{ q1, q2, …, qm }に関する一次写像fの行列表示　　


[文献]
・志賀『線形代数30講』26講(pp.164-6);

※一般化：実ベクトル空間のあいだの一次写像の行列表示に関する基底変換公式

※この定理はどこで使われるのか？： 一次写像の行列表示の標準化　

本題

「『Rnの基底』{ p1, p2, …, pn },『Rmの基底』{ q1, q2, …, qm }に関する一次写像fの行列表示」Bは、
　　・「『Rmの基底』を、『R mの標準基底』{ e'1, e'2, …, e'm }から{ q1, q2, …, qm }へ変えたときの基底変換行列」の逆行列Q－１　
　　・「『Rnの標準基底』{ e1, e2, …, en },『R mの標準基底』{ e'1, e'2, …, e'm }に関する一次写像fの行列表示」A　
　　・「『Rnの基底』を、『Rnの標準基底』{ e1, e2, …, en }から{ p1, p2, …, pn }へ変えたときの基底変換行列」P　
　の行列積に等しい。
すなわち、
　B=Q－１AP　


→[トピック一覧：基底変換と一次写像]
→線形代数目次・総目次		 　
定理：実n次元数ベクトル空間上の一次変換の行列表示に関する基底変換公式

設定
この定理は、以下の舞台設定上で成り立つ。
R：実数体(実数をすべて集めた集合）　　
Rn：実n次元数ベクトル空間。　
　　すなわち、Rn＝R×R×…×R＝{ ( v1, v2, …, vn )｜v1∈Rかつv2∈Rかつ…かつvn∈R }に、
　　　　　　　　ベクトルの加法とスカラー乗法を定義したもの。　
　　ただし、Rnに属すすべての実n次元数ベクトルは、n次元縦ベクトルの形式で表されているものとする。
{ e1, e2, …, en }：「Rnの標準基底」
{ p1, p2, …, pn }：「Rnの基底」の一つ。　
「f:Rn→Rn」：RnからRnへの一次変換
A： 「Rnの標準基底」{ e1, e2, …, en }に関する一次変換fの行列表示　　
B： 「Rnの基底」{ p1, p2, …, pn }に関する一次変換fの行列表示　　


[文献]
・松坂『解析入門4』18.1-Ａ命題2(p.85)：数ベクトル空間限定・証明つき;
・志賀『線形代数30講』26講(pp.164-6);
※一般化：実ベクトル空間上の一次変換の行列表示に関する基底変換公式

※この定理はどこで使うのか？：
　　・一次変換の行列表示の標準化の問題
　　・一次変換の行列表示の対角化の問題(固有値問題)　

　
本題 「Rnの基底」{ p1, p2, …, pn }に関する一次変換fの行列表示」Bは、
　　・「『Rnの基底』を、『Rnの標準基底』{ e1, e2, …, en }から{ p1, p2, …, pn }へ変えたときの基底変換の行列」の逆行列P－１
　　・「『Rnの標準基底』{ e1, e2, …, en }に関する一次変換fの行列表示」A
　　・「『Rnの基底』を、『Rnの標準基底』{ e1, e2, …, en }から{ p1, p2, …, pn }へ変えたときの基底変換の行列」P
　の行列積に等しい。
すなわち、
 　　B=P－１AP　　
つまり、
「Rnの基底」{ p1, p2, …, pn }に関する一次変換fの行列表示」Bは、
「『Rnの標準基底』{ e1, e2, …, en }に関する一次変換fの行列表示」Aに、
相似である。
証明 ※なぜ？→松坂『解析入門4』18.1-Ａ命題2(p.85)


→[トピック一覧：基底変換と一次写像]
→線形代数目次・総目次
　
定義：相似

設定
この定義は、以下の舞台設定上で成り立つ。
R：実数体(実数をすべて集めた集合）
A：実n次正方行列
B：実n次正方行列


[文献]
・斎藤『線形代数入門』４章§1-2(p.93);４章§5 (p.118);
・松坂『解析入門4』18.1-A(p.85);18.1-B(p.86)：数ベクトル空間限定;
・永田『理系のための線形代数の基礎』1.4(p.31);
・ホフマン･クンツェ『線形代数学I』3.4行列による一次変換の表現(p.97);
・岡田『経済学・経営学のための数学』2.6(p. 100).

※相似な行列の性質：
　・固有値について：相似な行列の固有値・固有ベクトル
　・
※活用例：行列の対角化可能/一次変換の対角化可能　
本題1 ・「実n次正方行列Aと実n次正方行列Bとは相似である」とは、
　　B=P－１AP
　を満たすn次正則行列Pが存在することをいう。
・「実n次正方行列Aと実n次正方行列Bとが相似である」ことを、
　記号「A～B」
　と表すこともある。
本題2 ・一次変換の行列表示に関する基底変換の公式とあわせて考えると、
　実n次正方行列Aが実n次正方行列Bに相似であるということは、
　任意の実ベクトル空間において、
　AとBは、
　同一の一次変換を異なった二つの基底に関して表した行列であること
　を意味する。[ホフマン･クンツェ『線形代数学I』(p.97)]
本題3 ・行列の相似について、以下の反射律・対称律・推移律が成り立つ。[証明→斎藤『線形代数入門』４章§1-2(p.93)]
　[反射律] 実n次正方行列Aはそれ自身と相似。A～A。　
　[対称律] 　「A～B」　⇒　「B～A」　　
　[推移律] 「実n次正方行列Aと実n次正方行列Bとが相似」かつ「実n次正方行列Bと実n次正方行列Cとが相似」　　　
　　　　　　ならば　
　　　　　　「実n次正方行列Aと実n次正方行列Cとは相似」　
　　　　　　　　　　「A～B　かつ　B～C」　⇒　「A～C」

・相似な行列は、トレース・固有値・行列式が共通。
　しかし、各行列のトレース・固有値・行列式が等しいからといって、それらの行列が相似であるとは限らない。[木村『線形代数：数理科学の基礎』4.1(pp.77-9)。]


→[トピック一覧：基底変換と一次写像]
→線形代数目次・総目次

　
定義：変換する　

設定
この定義は、以下の舞台設定上で成り立つ。
R：実数体(実数をすべて集めた集合）
A：実n次正方行列
P：実n次正方行列
[文献]
　・永田『理系のための線形代数の基礎』1.4(p.31);
　・ホフマン･クンツェ『線形代数学I』3.4行列による一次変換の表現(pp.93-94);
本題 実n次正方行列Aを実n次正方行列Pで変換するとは、
　Aから　P－１AP
をつくること。


→[トピック一覧：基底変換と一次写像]
→線形代数目次・総目次

　

(reference)
日本数学会編集『岩波数学辞典（第三版）』 岩波書店、1985年、項目83行列L線形写像(p.222)
線形代数のテキスト
志賀浩二『数学30講シリーズ：線形代数30講』朝倉書店、1988年、18講正則行列と基底変換(pp.115-8)。
ホフマン・クンツェ『線形代数学I』培風館、1976年、3.4行列による一次変換の表現(p.89)。
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、1.4行列と一次写像(pp.23-31)。
藤原毅夫『理工系の基礎数学2：線形代数』岩波書店、1996年、4.3線形写像の階数と行列の階数(p.102)。
斎藤正彦『線形代数入門』東京大学出版会、1966年、第2章§3行列と線形写像(p.44):実線形空間･複素線形空間のみ;。
佐武一郎『線形代数学(第44版)』裳華房、1987年、Ⅲベクトル空間§7ベクトル空間の公理化(pp.120-122)。

数理経済学のテキスト
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、§5.2.1線形写像の行列表現(p.165)。

→[トピック一覧：基底変換と１次写像]　
→線形代数目次・総目次