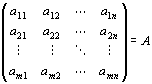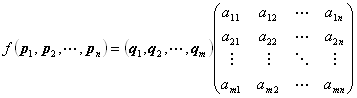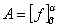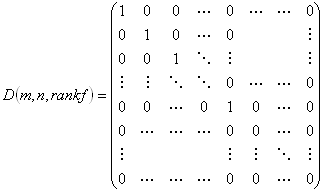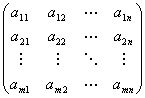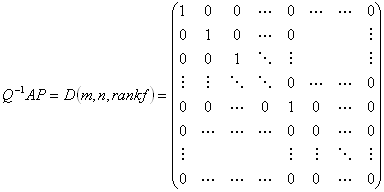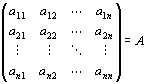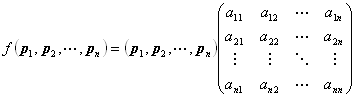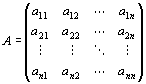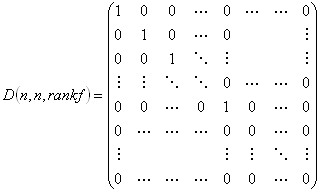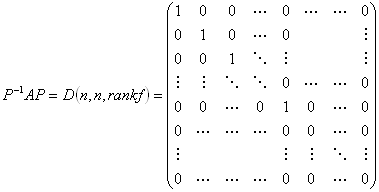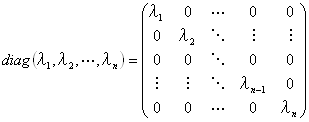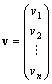設定
この定理は、以下の舞台設定上で成り立つ。
R:実数体(実数をすべて集めた集合)
A:(m,n)型実行列
Rn:実n次元数ベクトル空間。
すなわち、Rn=R×R×…×R={ ( v1, v2, …, vn )|v1∈Rかつv2∈Rかつ…かつvn∈R }に、
ベクトルの加法とスカラー乗法を定義したもの。
ただし、Rnに属すすべての実n次元数ベクトルは、n次元縦ベクトルの形式で表されているものとする。
v:実n次元縦ベクトル。
Rm:実m次元数ベクトル空間。
すなわち、Rm=R×R×…×R={ ( v1, v2, …, vm)|v1∈Rかつv2∈Rかつ…かつvm∈R }に、
ベクトルの加法とスカラー乗法を定義したもの。
ただし、Rmに属すすべての実m次元数ベクトルは、m次元縦ベクトルの形式で表されているものとする。
・永田『理系のための線形代数の基礎』1.4行列と一次写像:注意1(p.29);
・志賀『線形代数30講』7講:R2上の一次変換のケース(p.44)
[文献-解析学]
・松坂『解析入門4』15.1-E命題11 (p.10)
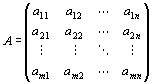
によって定義された一次写像を、f:Rn→Rmで表すと、
Rnの基本ベクトルe1, e2, …, enのfによる像 f(e1) , f(e2) , …, f(en) ∈Rm は、
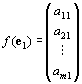
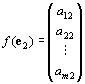
:
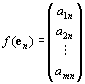
となる。