一般の線形空間(ベクトル空間)における一次写像の定義 : トピック一覧
・定義:一次写像・線形写像/像Image/核Kernel/階数rank/退化次数nullity/一次変換・線形変換・一次作用素・線形作用素/零写像
・定理:零写像は一次写像
【関連ページ : ベクトル空間一般における一次写像】
・一次写像:ベクトル演算の一次写像/一次写像の代数系/一次写像と一次独立/一次写像―全射・単射/階数/同型写像/同型写像と線形独立
・一次写像と行列の関係:一次写像の行列表示/基底の変換と一次写像と行列
【具体例:ベクトル空間における一次写像】実ベクトル空間から実ベクトル空間への一次写像/RnからRmへの一次写像・線形写像 /R2上の一次変換
定義:一次写像・線形写像linear mapping
[『岩波数学辞典』210線形空間:B線形写像(p.570);砂田『行列と行列式』§5.1c定義5.10(p.157);永田『理系のための線形代数の基礎』1.3(p.19);志賀『線形代数30講』16講(p.100); ホフマン『線形代数学I』3.1一次変換(pp.69-76);酒井『環と体の理論』1.6ベクトル空間(p.23);藤原『線形代数』4.1(p.93);]
(舞台設定)
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
V :K上のベクトル空間
V' :K上のベクトル空間
+:ベクトル空間Vにおいて定義されているベクトルの加法
+:ベクトル空間V'において定義されているベクトルの加法
スカラーに続けてベクトルを並べて書いたもの:K上のベクトル空間Vにおいて定義されているスカラー乗法
および、K上のベクトル空間V'において定義されているスカラー乗法
(本題)
「K上のベクトル空間VからK上のベクトル空間V'への写像f:V→V' が一次写像・線形写像である」とは、
K上のベクトル空間VからK上のベクトル空間V'への写像f:V→V' が、
次の二要件を満たすことをいう。
要件1: 写像f:V→V' がベクトル和を保存すること。
つまり、Vの任意のベクトルの(Vで定義された)和の「写像fがV'に写した像」と、
それらのベクトルの「写像fがV'に写した像」どおしの(V'で定義された)和とが、
一致すること。
(∀u,v∈V) ( f ( u+v )=f ( u )+f ( v ) )
要件2: 写像f:V→V' がスカラー倍を保存すること。
つまり、
「Vの任意のベクトル」の「Kの任意の元」による(Vで定義された)スカラー倍を、
「写像fによってV'に写した像」と、
そのベクトルの「写像fがV'に写した像」の
「Kの任意の元」による(V'で定義された)スカラー倍とが、
一致すること。
(∀v∈V) (∀a∈K) ( f (a v )=a f ( v ) )
※これを、一次変換・線形変換とよぶこともある。[ホフマン『線形代数学I』3.1一次変換(pp.69-76);]
※一次写像の諸属性:Image,核Kernel,階数rank,退化次数nullity
※関連:一次写像の行列表示
※下位概念:実ベクトル空間から実ベクトル空間への一次写像
定義:一次写像の像Image
[砂田『行列と行列式』§5.1c定義5.10(p.157);『岩波数学辞典』項目210-F(p.571); 永田『理系のための線形代数の基礎』1.6 (p.36);志賀『線形代数30講』21講(p.133);佐武『線形代数学』Ⅲ§4(p.103)]
(舞台設定)
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
V :K上のベクトル空間
V' :K上のベクトル空間
f:V→V':K上のベクトル空間VからK上のベクトル空間V'への一次写像
(定義)
一次写像f:V→V'の像Imageとは、定義域V全体のfによる像
{ f (v ) | v∈V }
のこと。
つまり、Vに属すあらゆるベクトルのfによる像をあつめた集合を、fの像と呼ぶ。
(記号)
一次写像fの像を、Image f , Im f などで表す。
(意義)
写像f:V→V' という概念は、
定義域V全体のfによる像が、終集合V'と必ずしも一致しなくてもよいものとして
定義されていた。(両者が一致する写像は、特に、全射と呼ばれる)
一次写像f:V→V'の定義は、
写像f:V→V' の概念に、ベクトル和保存・スカラー倍保存の演算則を付け加えただけのものだから、
一次写像f:V→V'の定義も、定義域V全体のfによる像が、終集合V'と一致することを要求していない。
つまり、一次写像f:V→V'には、定義域V全体のfによる像と終集合V'とが一致しないものが多く含まれている。
すると、終集合V'とは別に、定義域V全体のfによる像を検討すべき機会が多々でてくる。
そこで「定義域V全体のfによる像」の略称・記号として、「fの像」「Im f 」が用意されることになる。
(性質)
一次写像f:V→V'にたいして、
Image f は、V'の部分ベクトル空間となる。
※なぜ?→証明
※dim(Image f) を階数と呼ぶ。→詳細
(図解)
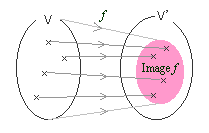
※下位概念:実ベクトル空間から実ベクトル空間への一次写像の像
定義:一次写像の核・核空間 Kernel
[砂田『行列と行列式』§5.1c定義5.10(p.157);ホフマン『線形代数学I』3.1一次変換(p.73); 『岩波数学辞典』項目210-F(pp.571-2);永田『理系のための線形代数の基礎』1.6 (pp.35-6); 志賀『線形代数30講』21講(p.133);佐武『線形代数学』Ⅲ§4(p.103)]
(舞台設定)
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
V :K上のベクトル空間
V' :K上のベクトル空間
f:V→V':K上のベクトル空間VからK上のベクトル空間V'への一次写像
(定義)
一次写像f:V→V'の核Kernelとは、fによる像がV'上の零ベクトルとなる「Vに属すベクトル」の集合。
つまり、V'上の零ベクトルのfによる逆像
f-1 (0)={ v∈V | f (v )=0 }
のこと。
(記号)
一次写像fの核を、Ker fで表す。
(性質)
一次写像f:V→V'にたいして、
Ker f は、Vの部分ベクトル空間である。
※なぜ?→証明
※dim(Ker f) を退化次数と呼ぶ。→詳細
※活用例:一次写像が単射(1対1写像)であるための必要十分条件、
(図解)
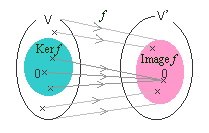
どんな一次写像f:V→V'であれ、V上の零ベクトルを、V'上の零ベクトルに写す。(∵)
だから、どんな一次写像f:V→V'にたいしても、Ker fには必ず、V上の零ベクトルが属す。
もし、一次写像fが、それ以外のV上のベクトルを、V'上の零ベクトルに写すなら、
それらのV上のベクトルもすべて、Ker fに属すことになる。
※下位概念:実ベクトル空間から実ベクトル空間への一次写像の核
定義:一次写像の階数 rank
[『岩波数学辞典』項目210-F(p.572);永田『理系のための線形代数の基礎』1.6 (p.37); ホフマン『線形代数学I』3.1一次変換(p.73);斎藤『線形代数入門』4章§5(p.116); 佐武『線形代数学』Ⅲ§4(p.105);砂田『行列と行列式』§5.5-d定義5.80(p.194). ]
(舞台設定)
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
V :K上のベクトル空間。ただし、有限次元。
V' :K上のベクトル空間。
f:V→V':K上のベクトル空間VからK上のベクトル空間V'への一次写像
(本題)
一次写像f:V→V'の階数rankとは、fの像[Image f ]の次元のこと。
すなわち、rank f = dim(Image f) と定義される。
(性質)
rank f≦dim V'
これは、
Ker f が「Vの部分ベクトル空間」であること(∵)と、
「Vの部分ベクトル空間」の次元は、Vの次元より大きくならないということによる。
※一次写像の階数の性質、行列の階数
※下位概念:実ベクトル空間から実ベクトル空間への一次写像の階数
定義:一次写像の退化次数 nullity
[『岩波数学辞典』項目210-F(p.572);藤原『線形代数』4.2(p.99);志賀『線形代数30講』21講(p.133); 佐武『線形代数学』Ⅲ§4(p.105:脚注)]
(舞台設定)
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
V :K上のベクトル空間。ただし、有限次元。
V' :K上のベクトル空間。
f:V→V':K上のベクトル空間VからK上のベクトル空間V'への一次写像
(本題)
一次写像f:V→V'の退化次数nullityとは、
fの核[Ker f ]の次元、すなわち、dim ( Ker f )
のこと。
(性質)
dim ( Ker f ) ≦dim V
これは、
Ker f が「Vの部分ベクトル空間」であること(∵)と、
「Vの部分ベクトル空間」の次元は、Vの次元より大きくならないということによる。
※下位概念:実ベクトル空間から実ベクトル空間への一次写像の退化次数
定義:一次変換・線形変換linear transformation 一次作用素・線形作用素
[『岩波数学辞典』210線形空間:B線形写像(p.570);永田『理系のための線形代数の基礎』1.3(p.20); ホフマン『線形代数学I』3.2一次変換の代数系(p.78);
(舞台設定)
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
V :K上のベクトル空間
(本題)
V上の一次変換・線形変換ないしVの一次作用素・線形作用素とは、
K上のベクトル空間VからV自身への一次写像f:V→V のことをいう。
※下位概念:実ベクトル空間から実ベクトル空間への一次変換
定義:零写像
[砂田『行列と行列式』§5.1c定義5.10(p.157);
(舞台設定)
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
V :K上のベクトル空間
V' :K上のベクトル空間
+:ベクトル空間Vにおいて定義されているベクトルの加法
+:ベクトル空間V'において定義されているベクトルの加法
スカラーに続けてベクトルを並べて書いたもの:K上のベクトル空間Vにおいて定義されているスカラー乗法
および、K上のベクトル空間V'において定義されているスカラー乗法
(本題)
「K上のベクトル空間VからK上のベクトル空間V'への写像f:V→V' が零写像である」とは、
Vの任意のベクトルの「写像fがV'に写した像」がすべて、V'の零ベクトルとなることをいう。
(∀x∈V) (∀a∈K) ( f (x )=〇 )
※下位概念:実ベクトル空間から実ベクトル空間への一次変換
定理:零写像は一次写像
[砂田『行列と行列式』§5.1c定義5.10(p.157); ]
(舞台設定)
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
V :K上のベクトル空間
V' :K上のベクトル空間
(本題)
K上のベクトル空間VからK上のベクトル空間V'への零写像は、一次写像の定義を満たす。
(reference)
日本数学会編集『岩波数学辞典(第三版)』 岩波書店、1985年、項目210線形空間(pp.570-576)
線形代数のテキスト
志賀浩二『数学30講シリーズ:線形代数30講』朝倉書店、1988年、16講線形写像(pp.100-105)。
ホフマン・クンツェ『線形代数学I』培風館、1976年、2.3基底と次元(pp.41-50)。
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、1.3ベクトル空間(pp.14-6)。
砂田利一『現代数学への入門:行列と行列式』2003年、§5.1-c(p.157);§5.5-d(p.194).
佐武一郎『線形代数学(第44版)』裳華房、1987年、Ⅲベクトル空間§4一次写像の階数(p.103)。
藤原毅夫『理工系の基礎数学2:線形代数』岩波書店、1996年、4.1線形空間と写像(p.93);4.2線形空間と写像(pp.98-9);
斎藤正彦『線形代数入門』東京大学出版会、1966年、第4章§5線形写像とくに線形変換(pp.113-9)。
代数学のテキスト
本部均『新しい数学へのアプローチ5:新しい代数』共立出版、1969年、5.2-Aベクトル空間(p.132)。
酒井文雄『共立講座21世紀の数学8:環と体の理論』共立出版、1997年、1.6ベクトル空間(p.22)。:数ページしか触れていないが、逆に、一般の線形空間の理論の骨組みだけを浮かびあがってくるので、何が重要事項なのかを見極める上で便利。
数理経済学のテキスト
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、§3.1ベクトル空間とは何か(p.105)。

