定義
1[
角度で方向を指定する場合の方向微分の定義-ベクトルを使わない表現]・「 n変数関数y=f (x1,x2,…,xn )は、点(a1, a2, …,an)において、
x1軸プラス方向に対して角度θ1方向
x2軸プラス方向に対して角度θ2方向
: :
xn軸プラス方向に対して角度θn方向
に方向微分可能である」
とは、
1変数関数φ(t)=f ( a1+t cosθ1 , a2+t cosθ2 , …, an+t cosθn ) について、
t =0における右微分係数
すなわち、
有限な右極限値
が存在することをいう。
・ n変数関数y=f (x1,x2,…,xn )は、点(a1, a2, …,an)において
x1軸プラス方向に対して角度θ1方向
x2軸プラス方向に対して角度θ2方向
: :
xn軸プラス方向に対して角度θn方向
に微分可能であるとき、
「f (x1,x2,…,xn )の点(a1, a2, …,an)における
x1軸プラス方向に対して角度θ1方向
x2軸プラス方向に対して角度θ2方向
: :
xn軸プラス方向に対して角度θn方向
の方向微分係数」
とは、
1変数関数φ(t)=f ( a1+t cosθ1 , a2+t cosθ2 , …, an+t cosθn ) の、
t =0における右微分係数
すなわち、
有限な右極限値
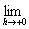
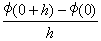
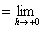
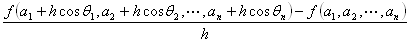
のことをいう。
[
文献-数学]・黒田『微分積分学』8.3.3定義8.10(pp.287) :n変数実数値関数;.
※方向微分係数の計算公式
※2変数関数の方向微分
※ベクトル値関数の方向微分
・「y= f ( x )は実n次元数ベクトルaにおいて
x1軸プラス方向に対して角度θ1方向
x2軸プラス方向に対して角度θ2方向
: :
xn軸プラス方向に対して角度θn方向
に微分可能」
とは、
実n次元数ベクトル e=( cosθ1 , cosθ2 , …, cosθn ) にたいして、
有限な右極限値
が存在することをいう。
* hは実数、
heは、実n次元数ベクトルeのスカラー倍、
a+he(θ) は、aとh eとのベクトル和を表す。
・y= f ( x )は実n次元数ベクトルaにおいて
x1軸プラス方向に対して角度θ1方向
x2軸プラス方向に対して角度θ2方向
: :
xn軸プラス方向に対して角度θn方向
に微分可能であるとき、
「aにおけるy= f ( x )のe方向微分係数」とは、
e=( cosθ1 , cosθ2 , …, cosθn ) にたいする有限な右極限値
のことを指す。
* hは実数、
heは、実n次元数ベクトルeのスカラー倍、
a+he は、aとh eとのベクトル和を表す。
・「aにおけるy= f ( x )のe方向微分係数」を、
e=( cosθ1 , cosθ2 , …, cosθn ) を用いて、
De f (a)
と表す。
[
文献-数学]・黒田『微分積分学』8.3.3定義8.10(pp.287) :n変数実数値関数;.
※方向微分係数の計算公式
※2変数関数の方向微分