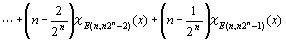定理:
非負実数値1変数関数に各点収束する関数列要旨
設定
この定理は、以下のように設定された舞台上で成立する。
Step2:Rの部分集合をひとつきめて、Dと名づける。
Step3:Dを定義域とする「非負実数値1変数関数」y= f (x)
つまり、
1変数関数「f:D→R」であって、
任意の x∈D⊂Rにたいして、f (x)≧0
を満たすもの
を用意する。
y= f (x) は有界関数でなくてもよいので、
たとえば、(0,1 ]を定義域とするy= f (x)=1/xなどでもよい。
[
文献]ルディン『現代解析学』10.20(p.267)。
志賀『ルベーグ積分30講』18講(p.138)):図解付,可測関数のケース。
新井『ルベーグ積分講義』定理7.12(p.103):図解付,可測関数のケース。
伊藤清三定理10.1(p.63):図解付,可測関数のケース。
Malliavin,Integration and Probability, 6.4.2Corollary(p.28);可測関数のケース。
定理
y= f (x)
に対して、
次のように定義された関数列{fn}={ f1 , f2 , f3 , … }は、[性質1] [性質2] [性質3]を満たす。
[関数列{ fn(x)}={ f1 , f2 , f3 , … }の定義]
Step1:関数fn(x)の定義
ある自然数nを一つ決める。
x軸上の「y = f (x) の定義域」Dを、
(n2n+1)個のR上の点集合
E(n,0) = f -1 ( [0/2n, 1/2n ) ) = { x ∈D⊂R | 0/2n≦f (x)<1/2n }
E(n,1) = f -1 ( [1/2n, 2/2n ) ) = { x ∈D⊂R | 1/2n≦f (x)<2/2n }
E(n,2) = f -1 ( [2/2n, 3/2n ) ) = { x ∈D⊂R | 2/2n≦f (x)<3/2n }
E(n,3) = f -1 ( [3/2n, 4/2n ) ) = { x ∈D⊂R | 3/2n≦f (x)<4/2n }
:
E(n,n2n−1) = f -1 ( [n−1/2n, n ) ) = { x ∈D⊂R | n−1/2n≦f (x)<n}
E(n) = f -1 ( [ n, +∞ ) ) = { x ∈D⊂R | n≦f (x) }
に切り分け、
これらの定義関数を用いて、
1変数関数fn(x)=0χE(n,0)(x)+(1/2n)χE(n,1) (x)+(2/2n )χE(n,2) (x)+(3/2n )χE(n,3) (x)+…
+nχE(n) (x)
を定義する。
Step2:関数列{fn(x)}の定義
・上記の1変数関数fnで、nを1とした
f1 (x)=0χE(1,0)(x)+(1/2)χE(1,1) (x)+1χE(1) (x)
・上記の1変数関数fnで、nを2とした
f2(x)=0χE(2,0)(x)+(1/4)χE(2,1) (x)+(1/2)χE(2,2) (x)+(3/4)χE(2,3) (x)+1χE(2,4) (x)
+(5/4)χE(2,5) (x)+(3/2)χE(2,6) (x)+(7/4)χE(2,7) (x)+2χE(2) (x)
・上記の1変数関数fnで、nを3とした
f3(x)=0χE(3,0)(x)+(1/8)χE(3,1) (x)+(1/4)χE(3,2) (x)+(3/8)χE(3,3) (x)+(1/2)χE(3,4) (x)
+(5/8)χE(3,5) (x)+(3/4)χE(3,6) (x)+(7/8)χE(3,7) (x)+χE(3,8) (x)
+(9/8)χE(3,9) (x)+(5/4)χE(3,10) (x)+(11/8)χE(3,11) (x)+(3/2)χE(3,12) (x)
+(13/8)χE(3,13) (x)+(7/4)χE(3,14) (x)+(15/8)χE(3,15) (x)+2χE(3,16) (x)
+(17/8)χE(3,17) (x)+(9/4)χE(3,18) (x)+(19/8)χE(3,19) (x)+(5/2)χE(3,20) (x)
+(21/8)χE(3,21) (x)+(11/4)χE(3,22) (x)+(23/8)χE(3,23) (x)
+3χE(3) (x)
:
:
という具合に、自然数nを一つずつ増やしながら、上記の1変数関数fnを並べていったものを、
関数列{ fn}= { f1 , f2 , f3 , … }
として定義する。
※この関数列{fn}={ f1 , f2 , f3 , … }について、もっと詳しい説明→詳細
[性質1] この関数列の各項 f1 , f2 , f3 , …は、すべて単関数。
※なぜ?→証明
[性質2] この関数列は、単調増加列。
つまり、
任意のx∈D⊂Rにたいして、
xを固定して得られる数列 { fn(x ) }={ f1 (x ) , f2 (x ) , f3 (x ) , … } が、
f1 (x )≦f2 (x )≦f3 (x )≦…
を満たす。
※なぜ?→証明
[性質3] この関数列{ f1 , f2 , f3 , … }は、1変数関数f に各点収束する。
※なぜ?→証明