1変数関数の関数列･関数項級数の極限の定義：トピック一覧　　

　・定義：関数列の定義/関数項級数の定義　　
　・定義：一点における関数列の収束と発散/一点における関数項級数の収束と発散
　　　　　区間における関数列の各点収束･極限関数/区間における関数項級数の各点収束･和　
　　　　　区間における関数列の一様収束/区間における関数項級数の一様収束　

　※1変数関数からなる関数列関連ページ：一様収束判定条件/極限関数の連続性/関数列の極限と積分/単関数列近似　　
　※一般化：実数値関数一般の関数列・関数項級数とその極限の定義　　
　※総目次

定義： 関数列sequence of functions

定義

区間I上の関数列とは、
区間I上で定義された関数の無限列f1(x),f2(x),…のことをいい、
{ fn(x)}{ fn}などと表記する。
また、数列の場合と同様、
関数列を構成するおのおのの関数を項とよぶ。

[文献]
吹田新保『理工系の微分積分学』第5章3節(p.137);
小平『解析入門I』p.214
黒田『微分積分』第3章5節(p.113)
ルディン『現代解析学』7.1(p.145)。

例

・fn(x)＝xnとしたときの、関数列{ fn(x)}={ x, x2, x3,…xn,…}

定義： 関数項級数Series of Functions

定義

区間I上の関数列{ fn(x)}からつくられた級数
　　　
を関数項級数とよぶ。

　

[文献]
吹田新保『理工系の微分積分学』第5章3節(p.139);
小平『解析入門I』p.217.
黒田『微分積分』第3章5節(p.113)
　 　

→[トピック一覧：関数列の極限]
→総目次

定義： 特定の一点における関数列の収束と発散

設定

関数列{ fn(x)}：それぞれの関数f1(x), f2(x),…は、区間I上で定義されているとする。
x 0　　　　　：区間I上の特定の一点。　つまり、x 0∈I　
{ fn(x 0)}　　　：関数列{ fn(x)}={ f1(x), f2(x), f3(x),…}を、x= x 0　としたもの。
　　　　　　　　　{ fn(x 0)}={ f1(x 0), f2(x 0), f3(x 0),…}は、ただの数列となる。　

[文献]
吹田新保『理工系の微分積分学』第5章3節(p.138);
小平『解析入門I』p.215;
黒田『微分積分』第3章5節(p.113)

定義

関数列{ fn(x)}がx= x 0で値αに収束するとは、　　　
　　　数列{ fn(x 0)}={ f1(x 0), f2(x 0), f3(x 0),…}がαに収束することである。　　
これを、記号
　　　
で表す。　

定義

関数列{ fn(x)}がx= x 0で発散するとは、　　　
　　　数列{ fn(x 0)}が発散することである。　　　

例

fn(x)＝xnとしたときの、関数列{ fn(x)}={ x, x2, x3,…xn,…}は、x=1/2で、０に収束する。
fn(x)＝xnとしたときの、関数列{ fn(x)}={ x, x2, x3,…xn,…}は、x=1/3で、０に収束する。
fn(x)＝xnとしたときの、関数列{ fn(x)}={ x, x2, x3,…xn,…}は、x=1/4で、０に収束する。
　　つまり、　
　　　　

定義： 特定の一点における関数項級数の収束と発散

設定

関数列{ fn(x)}：それぞれの関数f1(x), f2(x),…は、区間I上で定義されているとする。
部分和sm(x)　：関数列{ fn(x)}の第1項から第m項までの和。
　　　　　　　　つまり、sm(x)=f1(x)+f2(x)+…+ fm(x)　
部分和列{ sm(x)}：{ s1(x), s2(x), s3(x),…}={ f1(x), f1(x)+f2(x), f1(x)+f2(x) +f3(x),…}
　　　　　　　　　のこと。これも関数列。　
x 0　　　　　：区間I上の特定の一点。　つまり、x 0∈I　
{ fn(x 0)}　　　：関数列{ fn(x)}={ f1(x), f2(x), f3(x),…}を、x= x 0　としたもの。
　　　　　　　　　{ fn(x 0)}={ f1(x 0), f2(x 0), f3(x 0),…}は、ただの数列となる。　

[文献]
吹田新保『理工系の微分積分学』第5章3節(p.139);
小平『解析入門I』p.217;
黒田『微分積分』第3章5節(p.120)

定義

関数列{ fn(x)}の関数項級数がx= x 0で値αに収束するとは、　　　
　部分和列
　　{ sm(x0) } = { s1(x 0) , s2(x 0), s3(x 0),…}
　　　　　　= { f1(x 0), f1(x 0)+f2(x 0), f1(x 0)+f2(x 0) +f3(x 0),…}
　がαに収束することである。　　
これを、記号
　　　　
で表す。　

定義

関数列{ fn(x)}がx= x 0で発散するとは、　　　
　部分和列
　　{ sm(x0) } = { s1(x 0) , s2(x 0), s3(x 0),…}
　　　　　　= { f1(x 0), f1(x 0)+f2(x 0), f1(x 0)+f2(x 0) +f3(x 0),…}
が発散することである。
　 　

→[トピック一覧：関数列の極限]
→総目次

定義： 区間I上での関数列の収束(各点収束pointwise convergence)、極限関数

設定

関数列{ fn(x)}：それぞれの関数f1(x), f2(x),…は、区間I上で定義されているとする。
x 0　　　　　：区間I上の一点。　つまり、x 0∈I　
{ fn(x 0)}　　　：関数列{ fn(x)}={ f1(x), f2(x), f3(x),…}を、x= x 0　としたもの。
　　　　　　　　　{ fn(x 0)}={ f1(x 0), f2(x 0), f3(x 0),…}は、ただの数列となる。　


[文献]
吹田新保『理工系の微分積分学』第5章3節(p.138);
小平『解析入門I』p.215;
黒田『微分積分』第3章5節(p.113);

ルディン『現代解析学』7.1(p.145):一般の集合上で定義された複素数値関数の関数列について。
杉浦『解析入門I』I§6定義9(p.62);Ⅳ§13(p.301):ベクトル値関数の関数列について;。

定義

関数列{ fn(x)}={ f1(x), f2(x), f3(x),…}が
区間I上で関数f(x)に収束(各点収束pointwise convergence)するとは、
∀x 0∈Iにたいして（I上の点x 0のすべての採り方にたいして）、
数列{ fn(x 0)}={ f1(x 0), f2(x 0), f3(x 0),…}が、f (x 0)に収束することである。
　　　　
また、この収束先のf (x)を、極限関数と呼ぶ。

厳密な
定義

関数列{ fn(x)}が区間I上で関数f(x)に収束(各点収束)する
とは、
関数列{ fn(x)}において、
任意のx∈Iと任意の（どんな小さな）正の実数εに対して（でも）、
　　　　　　　　　　（つまり、εを1でも、0.1でも、0.00…001まで狭めても）
　　　　　　 「　n≧Nならば、　| fn(x)－f (x)|＜ε　」
　　すなわち、「　n≧Nならば、　f (x)－ε＜fn(x)＜f (x)＋ε　」
　　すなわち、「　n≧Nならば、　　fn(x)∈ ( f (x)－ε, f (x)＋ε)　」
　　すなわち、「　n≧Nならば、　　fn(x)∈Uε(f (x))　」　※Uε(α): f (x)のε近傍
を成り立たせる、
ある（十分大きな）自然数Nが存在する、
ということである。
すなわち、(∀x∈I) (∀ε>0)(∃N∈N)(∀n∈N)( n≧N⇒| fn(x)－f (x)|＜ε)

※

x∈Iの採り方によって、Nの値が違っても、各点収束するといってよい。
Cf.一様収束：どのようにx∈Iをとっても、xの値に関わりなく、共通のNをとれなければならない。

例

fn(x)＝xnとしたときの、関数列{ fn(x)}={ x, x2, x3,…xn,…}は、
　　右半開区間[0,1)で、関数f(x)=０ に各点収束する。
※図解→黒田『微分積分』例3.22-図3.6 (p.115).

→[トピック一覧：関数列の極限]
→総目次

定義： 区間I上での関数項級数の各点収束pointwise convergence

設定

関数列{ fn(x)}：それぞれの関数f1(x), f2(x),…は、区間I上で定義されているとする。
部分和sm(x)　：関数列{ fn(x)}の第1項から第m項までの和。
　　　　　　　　つまり、sm(x)=f1(x)+f2(x)+…+ fm(x)　
部分和列{ sm(x)}：{ s1(x), s2(x), s3(x),…}={ f1(x), f1(x)+f2(x), f1(x)+f2(x) +f3(x),…}
　　　　　　　　　のこと。これも関数列。　
x 0　　　　　：区間I上の特定の一点。　つまり、x 0∈I　
{ fn(x 0)}　　　：関数列{ fn(x)}={ f1(x), f2(x), f3(x),…}を、x= x 0　としたもの。
　　　　　　　　　{ fn(x 0)}={ f1(x 0), f2(x 0), f3(x 0),…}は、ただの数列となる。　

[文献]
吹田新保『理工系の微分積分学』第5章3節(p.139);
小平『解析入門I』p.217;
黒田『微分積分』第3章5節(p.120)

ルディン『現代解析学』7.1(p.145):一般の集合上で定義された複素数値関数の関数項級数について。
杉浦『解析入門I』I§6定義9(p.62):ベクトル値関数の関数項級数について;。

定義

関数列{ fn(x)}の関数項級数がs(x)に収束するとは、　　　
　部分和列
　　　{ sm(x)}={ s1(x), s2(x), s3(x),…}
　　　　　　　={ f1(x), f1(x)+f2(x), f1(x)+f2(x) +f3(x),…}
　が、s(x)に関数列として各点収束すること。
また、s(x)を関数項級数の和とよぶ。　
これを、記号
　　
で表す。　
　 　

→[トピック一覧：関数列の極限]
→総目次

定義： 区間I上での関数列の一様収束uniform convergence

設定

関数列{ fn(x)}：それぞれの関数f1(x), f2(x),…は、区間I上で定義されているとする。
x 0　　　　　：区間I上の一点。　つまり、x 0∈I　
{ fn(x 0)}　　　：関数列{ fn(x)}={ f1(x), f2(x), f3(x),…}を、x= x 0　としたもの。
　　　　　　　　　{ fn(x 0)}={ f1(x 0), f2(x 0), f3(x 0),…}は、ただの数列となる。　

[文献]
小平『解析入門I』p.218;
黒田『微分積分』第3章5節(p.113-4);

ルディン『現代解析学』7.7(p.148):一般の集合上で定義された複素数値関数の関数列について。
杉浦『解析入門I』I§6定義9(p.62);Ⅳ§13定義1(p.302):ベクトル値関数の関数列について;。

定義

関数列{ fn(x)}={ f1(x), f2(x), f3(x),…}が区間I上で関数f(x)に一様収束するとは、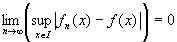
　　　　
が成り立つことである。

厳密な
定義

関数列{ fn(x)}が区間I上で関数f(x)に一様収束する
とは、
関数列{ fn(x)}において、
任意の（どんな小さな）正の実数εに対して（でも）、
　　　　　　　　　　（つまり、εを1でも、0.1でも、0.00…001まで狭めても）
　　　　　　 「　∀x∈I かつ n≧Nならば、　| fn(x)－f (x)|＜ε　」
　　すなわち、「　∀x∈I かつ n≧Nならば、　f (x)－ε＜fn(x)＜f (x)＋ε　」
　　すなわち、「　∀x∈I かつ n≧Nならば、　fn(x)∈ ( f (x)－ε, f (x)＋ε)　」
　　すなわち、「　∀x∈I かつ n≧Nならば、　fn(x)∈Uε(f (x))　」
　　　　　　　　　　　　　　　　　　　　　　　　※Uε(α): f (x)のε近傍
を成り立たせる、
ある（十分大きな）自然数Nが存在する、
ということである。
すなわち、(∀ε>0)(∃N∈N) (∀x∈I) (∀n∈N)( n≧N⇒| fn(x)－f (x)|＜ε)

※

一様収束の定義は、
どのようにx∈Iをとっても、xの値に関わりなく、共通のNをとれなければならないことを意味している。
これに対して、各点収束では、 x∈Iの採り方によって、Nの値が違っても良い。
関数列の各点収束と一様収束の関係は、関数の区間連続性と一様連続性の関係に似ている。

→[トピック一覧：関数列の極限]
→総目次

定義： 区間I上での関数項級数の一様収束

設定

関数列{ fn(x)}：それぞれの関数f1(x), f2(x),…は、区間I上で定義されているとする。
部分和sm(x)　：関数列{ fn(x)}の第1項から第m項までの和。
　　　　　　　　つまり、sm(x)=f1(x)+f2(x)+…+ fm(x)　
部分和列{ sm(x)}：{ s1(x), s2(x), s3(x),…}={ f1(x), f1(x)+f2(x), f1(x)+f2(x) +f3(x),…}
　　　　　　　　　のこと。これも関数列。　
x 0　　　　　：区間I上の特定の一点。　つまり、x 0∈I　
{ fn(x 0)}　　　：関数列{ fn(x)}={ f1(x), f2(x), f3(x),…}を、x= x 0　としたもの。
　　　　　　　　　{ fn(x 0)}={ f1(x 0), f2(x 0), f3(x 0),…}は、ただの数列となる。　

[文献]
吹田新保『理工系の微分積分学』第5章3節(p.139);
小平『解析入門I』p.217;
黒田『微分積分』第3章5節(p.120)

ルディン『現代解析学』7.7(p.149):一般の集合上で定義された複素数値関数の関数項級数について。
杉浦『解析入門I』Ⅳ§13(p.304):ベクトル値関数の関数項級数について;。

定義

関数列{ fn(x)}の関数項級数がs(x)に一様収束するとは、　　　
　部分和列
　　　{ sm(x)}={ s1(x), s2(x), s3(x),…}
　　　　　　　={ f1(x) , f1(x)+f2(x) , f1(x)+f2(x) +f3(x) , … }
　が、s(x)に関数列として一様収束すること。
　 　

→[トピック一覧：関数列の極限]
→総目次

　

(reference)

吹田・新保『理工系の微分積分学』学術図書出版社、1987年、第5章3節(pp.137-9). 標準的。
小平邦彦『解析入門I』 (軽装版)岩波書店、2003年、第5章3節a)(pp.214-215.)。標準的。
黒田成俊『21世紀の数学1:微分積分』共立出版、2002年、第3章5節(pp.112-114.)。標準的。非常に丁寧。
Walter Rudin, Principles of Mathematical Analysis,Mcgraw-Hill,1953-1976.
=ウォ－ルタ－・ルディン『現代解析学』共立出版、1971年、第7章7.1-:。ただ定義と定理を説明するのではなく、関数列で扱う主要問題と狙いを深いところから説明していて助かる。特に、連続関数列の極限が連続であるかどうかという問題が、極限の順序交換可能性の問題にほかならないなどとあらかじめ説明している点。
高橋一『経済学とファイナンスのための数学』新世社、1999年、第2章2.1節I(p.43):10行だけの説明。
Fischer,Emanuel.Intermediate Real Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Heidelberg Berlin,1983,ChapterXI-II.

　

→[トピック一覧：関数列の極限]
→総目次