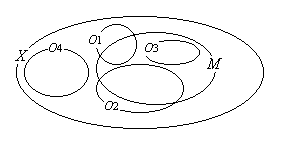相対位相・部分位相空間の定義
※位相関連ページ：開集合系・開集合、閉集合系・閉集合、近傍系・近傍、
開核作用素・開核、閉包作用素・閉包
位相空間・位相の定義、誘導位相
コンパクト
→
総目次
定義：
相対位相 relative topology、部分位相空間topological subspace、部分空間subspace
[松坂『集合・位相入門』第4章§5.B.(pp.188-9);彌永『集合と位相』II.位相第2章位相空間§2.8誘導位相(pp.212-4);
矢野『距離空間と位相構造』2.2.1相対位相(p.46); 斉藤『数学の基礎：集合・数・位相』項目4.1.1 8(p.106);
西村『経済数学早わかり』第6章位相数学§2.4部分位相空間(pp.291-5);
佐久間『集合･位相』3.6節p.71;73。志賀『位相への30講』第27講コンパクト空間と連結空間(pp.190-1)。]
[定義1:はじめに読むべき定義]
(設定)
X: (普遍)集合
O : Xの開集合系
(X, O) : 位相空間
Ｍ: Xの部分集合（ただし空集合ではないとする）
(本題)
Xの開集合系Oから、以下の手順で、Mの部分集合系OMをつくる。
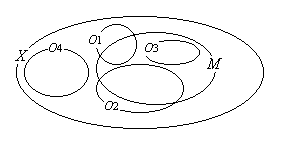
手順1: Oに属す全ての開集合について、Mとの重複部分を取った集合をつくる。
つまり、任意のO∈Oにたいして、O∩M をつくる。
※ここでつくった集合は、すべて、Mの部分集合である。
手順2：手順1でつくった集合をすべてかき集めて、集合系OMをつくる。
つまり、OM={O∩M|O∈O }
※任意のO∈Oにたいして、O∩MはMの部分集合であるから、
集合系OMは、、Mの部分集合系である。
このようにしてXの開集合系Oから作ったMの部分集合系OMは、Mの開集合系となる。（なぜ？→証明）
OMがMの開集合系となるなら、
位相・位相空間の定義より、OMは、Mに位相を与え、(M, OM)は位相空間となる。
上記手順1-2に従って，Xの開集合系Oから作ったMの開集合系OMを、MにおけるOの相対位相とよび、
MとOMとの対(M, OM)を、(X, O) の部分位相空間ないし(X, O) の部分空間とよぶ。
[定義2:厳密な定義]
[松坂『集合・位相入門』第4章§5.B.(pp.188-9); 佐久間『集合･位相』3.6節p.73]
(設定)
X: (普遍)集合
(X, O) : 位相空間
Ｍ: Xの部分集合（ただし空集合ではないとする）
i： MからXへの標準的単射。
（Mの各元にその元自身を対応づけるMからXへの1対1写像）
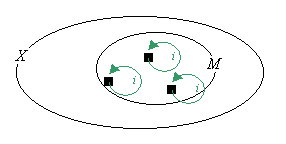
(本題)
MにおけるOの相対位相とは、
MからXへの標準的単射iによって、Xの位相Oから誘導されるMの位相OMのこと。
※では、i：M→XのによってXの位相Oから誘導されるMの位相OMとは？
以下の手順で、Mの部分集合系OMをつくる。
手順1: Xの位相Oに属す全ての開集合Oについて、i：M→Xの逆像i−1(O)をとっていく。
手順2: i−1(O)を、すべてあつめて、Mの部分集合系OMとする。
つまり、
OM ={ i−1(O) |O∈O}
このMの部分集合系OMは、Mの開集合系となるので（なぜ？→証明）、
OMは、Mにおける位相となり、位相空間 (M, OM)が成立する。
以上のようにXの位相OからつくられたMの位相OM={ i−1(O) |O∈O}が、
i：M→XによってXの位相Oから誘導されるMの位相OM={ i−1(O) |O∈O}である。
※Xの位相Oに属す全ての開集合Oについてi−1(O)= O∩Mであるから、
相対位相の定義2:OM={ i−1(O) |O∈O}は、
相対位相の定義1: OM={O∩M|O∈O }とまったく同じになる。
[
定義1でOMがMの開集合系となることの証明]
[斉藤『数学の基礎：集合・数・位相』項目4.1.1 8(p.106);]
(設定)
X: (普遍)集合
O : Xの開集合系
(X, O) : 位相空間
Ｍ: Xの部分集合（ただし空集合ではないとする）
OM={O∩M|O∈O }
(本題) OMがＭの開集合系であるための3条件を満たすことを示す。
Step1 : OMは条件1「M, φ∈OM」を満たす。
O はXの開集合系であるとされた。したがって、Oは条件1「X,φ∈O」を満たす。
したがって、OM={O∩M|O∈O } には、O= X,φ としたときのO∩Mも属していることになる。
すなわち、O=Xとしたとき、O∩M= X∩M=M∈OM
O=φとしたとき、O∩M =φ∩M=φ∈OM
よって、OMは条件1「M,φ∈OM」を満たす。
Step2: OMは条件2「(∀O'1,O'2∈ OM) (O'1∩O'2∈OM)」を満たす。
Step2-1: 任意のO1,O2∈Oに対してO1∩O2∈Oである。
(∵O はXの開集合系であるから、開集合系の条件2を満たす)
したがって、
OM={O∩M|O∈O } には、
O= O1∩O2としたときのO∩Mも属していることになる。
すなわち、O= O1∩O2としたとき、O∩M =(O1∩O2)∩M∈OM
よって、任意のO1,O2∈Oに対して、(O1∩O2)∩M∈OM …(2-1)
Step2-2: OMの定義より、
任意のO'1,O'2∈ OMには、必ず、何らかのO1,O2∈Oが存在して、
O'1= O1∩M、O'2= O2∩Mと書ける。
したがって、
任意のO'1,O'2∈ OMに対して、
O'1∩O'2=(O1∩M)∩(O2∩M)
=(O1∩O2)∩(M∩M) ∵結合則
=(O1∩O2)∩M ∵ベキ等律
ここのO1,O2は、何らかのO1,O2∈Oであったから、
(2-1)を適用できて、(O1∩O2)∩M∈OM
よって、O'1∩O'2∈OM
Step3: OMは条件3「 OMに属す「Xの部分集合」のみからなる
任意の「Xの部分集合族」O'λ(λ∈Λ)の和集合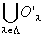
も、OMに属す。」
を満たす。
Step3-1: Oに属す「Xの部分集合」のみからなる
任意の「Xの部分集合族」Oλ(λ∈Λ)の和集合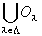
も、Oに属す。
つまり、任意のOλ∈O (λ∈Λ)に対して、
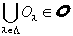
(∵O はXの開集合系であるから、開集合系の条件3を満たす)
したがって、
OM={O∩M|O∈O } には、
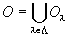としたときのO∩Mも属していることになる。
すなわち、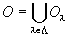としたとき、
O∩M
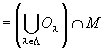
∈OM
よって、任意のOλ∈O (λ∈Λ)に対して、
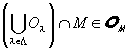…(3-1)
Step3-2: OMに属す「Xの部分集合」のみからなる任意の「Xの部分集合族」を、O'λ(λ∈Λ)とおく。
OMの定義より、
任意のλ∈Λに対して、O'λ∈ OMには、必ず、何らかのOλ∈Oが存在して、
O'λ= Oλ∩Mと書ける。
すると、
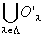
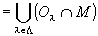
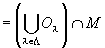∵集合族の分配律
ここのOλは何らかのOλ∈Oであったから、
Oλ∈O (λ∈Λ)は、Oに属す「Xの部分集合」のみからなるの「Xの部分集合族」のひとつ。
すると、(3-1)を適用できて、
→
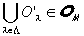
[トピック一覧：位相空間・位相の定義]
→
総目次
Reference
日本数学会編集『
岩波数学事典(第三版)』岩波書店、1985年、項目14位相空間。
矢野公一『距離空間と位相構造』共立出版、1997年。 2章位相空間2.1位相構造2.1.1位相(pp.56-62)
斉藤正彦『数学の基礎：集合・数・位相』東大出版会、2002年。第4章位相空間(その1)§1位相空間の定義・開集合と閉集合4.1.1-(pp.99-)
松坂和夫『集合・位相入門』岩波書店、1968年。第4章§2位相空間(pp.152-165)。P.164での著者による注意を読みおとさないように。
彌永昌吉・彌永健一『岩波講座基礎数学：集合と位相 I・II』 岩波書店、1977年。 II.位相第2章位相空間§2.1閉包写像と位相空間-§2.3近傍(pp.173-190)
志賀浩二『位相への30講』朝倉書店、1988年、第24講位相空間(pp.166-172)。
佐久間一浩『集合・位相―基礎から応用まで―』共立出版、2004年、p.71。
西村和雄『経済数学早わかり』日本評論社、1982年、第6章位相数学§1位相空間とは1.1-1.2。(pp.272-8)。卑近な例もまじえつつ、具体的に説明。
→
[トピック一覧：位相空間・位相の定義]
→
総目次
