・志賀『ルベーグ積分30講』第4講ふつうの面積概念―ジョルダン測度―(pp.24-29)。
[内面積という用語を使わない→吹田新保『理工系の微分積分学』191;]
(1)初めに読むべき定義
(舞台設定)
A: Aは、R2上の有界な点集合 を表すとする。
K: Kは、Aを内部に含むR2上の閉区間 { (x,y) | a≦x≦b, c≦y≦d }=[a,b]×[c,d]を表すとする。
Kij: Kの分割⊿によってできたmn個の小矩形を
Kij ={ (x,y) | xi-1≦x≦xi , yj-1≦y≦yj }=[ xi-1, xi ]×[ yj-1, yj ] ( i=1,2,…,m, j=1,2,…,n )
ただし、x0= a, xm=b, y0= c, yn =dとする。
で表すとする。
(本題-1)
有界な点集合Aとの重なり具合で、mn個ある小矩形 Kijを、3タイプに分類できる。
タイプ1:すべて点集合Aと重なる小矩形、
タイプ2:一部点集合Aと重なるが、一部Aとは重ならない小矩形、
タイプ3:すべて点集合Aと重ならない小矩形、
このうち、
タイプ1:すべて点集合Aと重なる小矩形
のみをすべてあつめてきて、
それら小矩形の面積を足し合せたもの
を s⊿ で表すことにする。
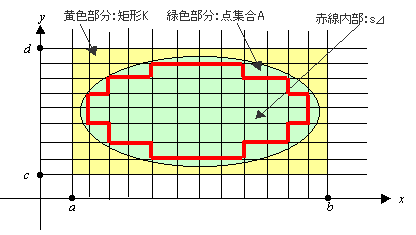
(本題-2)
Kの分割⊿を細かくしていく。すると、(上の図を見ながら考えよ)
タイプ1:すべて点集合Aと重なる小矩形 →それらの面積の合計 s⊿ が増える(タイプ2を奪うから)。
タイプ2:一部点集合Aと重なるが、一部Sとは重ならない小矩形
→それらの面積の合計が減る(タイプ1, 2へ流出)
タイプ3:すべて点集合Aと重ならない小矩形 →それらの面積の合計が増える(タイプ2を奪うから)
(本題-3)
点集合Aの内面積sとは、
Kの分割⊿を限りなく細かくしていき、 s⊿ を増やしていった際の、
s⊿の上限を指す。
すなわち、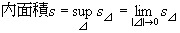
(2)特性関数(定義関数)を用いた表現
(舞台設定)
A: Aは、R2上の有界な点集合 を表すとする。
K: Kは、Aを内部に含むR2上の閉区間 { (x,y) | a≦x≦b, c≦y≦d }=[a,b]×[c,d]を表すとする。
P: Pは、R2上の点を表すとする。
χA(P):点集合Aの特性関数ないし定義関数
すなわち、
┌ χA(P)=1 (P∈A)
└ χA(P)=0 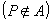
(本題)
(1)で述べたs⊿は、R2上の閉区間(閉矩形)Kにおける関数χA(P)の不足和、
内面積sは、R2上の閉区間(閉矩形)Kにおける関数χA(P)の下積分
に等しくなる。
※なぜか?→ 不足和、下積分の定義に立ちかえって、(1)の説明と一致することを確かめよ。
定義:外面積(ジョルダン外測度)
[高木『解析概論』第8章91節(p.327.);片山孝次『微分積分学』p.203;小平『解析入門II』348-9.
志賀『ルベーグ積分30講』第4講ふつうの面積概念―ジョルダン測度―(pp.24-29)。]
[外面積という用語を使わない→吹田新保『理工系の微分積分学』191;]
(1)初めに読むべき定義
(舞台設定)
A: Aは、R2上の有界な点集合 を表すとする。
K: Kは、Aを内部に含むR2上の閉区間 { (x,y) | a≦x≦b, c≦y≦d }=[a,b]×[c,d]を表すとする。
Kij: Kの分割⊿によってできたmn個の小矩形を
Kij ={ (x ,y ) | xi-1≦x≦xi , yj-1≦y≦yj }=[ xi-1, xi ]×[ yj-1, yj ] (i=1,2,…,m, j=1,2,…,n )
ただし、x0= a, xm=b, y0= c, yn =dとする。
で表すとする。
(本題-1)
有界な点集合Aとの重なり具合で、mn個ある小矩形 Kijを、3タイプに分類できる。
タイプ1:すべて点集合Aと重なる小矩形、
タイプ2:一部点集合Aと重なるが、一部Aとは重ならない小矩形、
タイプ3:すべて点集合Aと重ならない小矩形、
このうち、
タイプ1:すべて点集合Aと重なる小矩形、
タイプ2:一部点集合Aと重なるが、一部Aとは重ならない小矩形
のみをすべてあつめてきて、
それら小矩形の面積を足し合せたもの
を S⊿ で表すことにする。
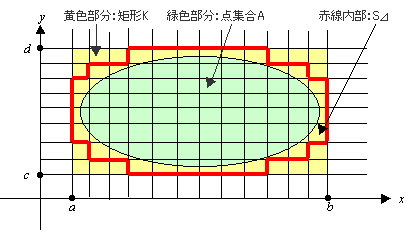
(本題-2)
Kの分割⊿を細かくしていく。すると、(上の図を見ながら考えよ)
タイプ1:すべて点集合Aと重なる小矩形 →それらの面積の合計s⊿ が増える(タイプ2を奪うから)。
タイプ2:一部点集合Aと重なるが、一部Sとは重ならない小矩形
→それらの面積の合計が減る(タイプ1, 2へ流出)
タイプ3:すべて点集合Aと重ならない小矩形 →それらの面積の合計が増える(タイプ2を奪うから)
となるので、
タイプ1とタイプ2を足し合せた S⊿ 全体の面積は、減少してゆく。
(本題-3)
点集合Aの外面積Sとは、
Kの分割⊿を限りなく細かくしていき、 S⊿ を減らしていった際の、
S⊿ の下限を指す。
すなわち、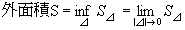
(2)特性関数(定義関数)を用いた表現
(舞台設定)
A: Aは、R2上の有界な点集合 を表すとする。
K: Kは、Aを内部に含むR2上の閉区間(閉矩形) { (x ,y ) | a≦x≦b, c≦y≦d }=[a,b]×[c,d]を表すとする。
P: Pは、R2上の点 を表すとする。
χA(P):点集合Aの特性関数ないし定義関数
すなわち、
┌ χA(P)=1 (P∈A)
└ χA(P)=0 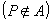
(本題)
(1)で述べたS⊿は、R2上の閉区間(閉矩形)Kにおける関数χA(P)の過剰和、
外面積Sは、R2上の閉区間(閉矩形)Kにおける関数χA(P)の上積分
に等しくなる。
※なぜか?→ 過剰和、上積分の定義に立ちかえって、(1)の説明と一致することを確かめよ。
→総目次
定義:面積(ジョルダン測度)、面積確定(ジョルダン可測)
[高木『解析概論』第8章91節(p.327.);吹田新保『理工系の微分積分学』192;杉浦『解析入門I』IV章§8(pp.255-256.);
笠原『微分積分学7.2節[2]定義7.1.7(p.259.);片山孝次『微分積分学』p.203;小平『解析入門II』348-9.
志賀『ルベーグ積分30講』第4講ふつうの面積概念―ジョルダン測度―(pp.24-29)。]
(1)初めに読むべき定義
・「点集合Aが面積確定(ジョルダン可測)である」とは、
点集合Aの内面積s=点集合Aの外面積S
となることをいう。
・「点集合Aの面積(ジョルダン測度)」とは、
点集合Aが面積確定であるときの、
内面積s=外面積S
の値を指す。
(2)特性関数(定義関数)を用いた表現
(舞台設定)
A: Aは、R2上の有界な点集合 を表すとする。
K: Kは、Aを内部に含むR2上の閉区間(閉矩形) { (x,y) | a≦x≦b, c≦y≦d }=[a,b]×[c,d]を表すとする。
P: Pは、R2上の点 を表すとする。
χA(P):点集合Aの特性関数ないし定義関数
すなわち、
┌ χA(P)=1 (P∈A)
└ χA(P)=0 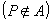
(本題)
・「点集合Aが面積確定(ジョルダン可測)である」とは、
R2上の閉区間(閉矩形)Kにおける関数χA(P)について、ダルブーの可積分条件が成り立って、
χA(P)が、K上リーマン積分可能となることをいう。
・「点集合Aの面積」とは、
χA(P)の、R2上の閉区間(閉矩形)Kにおける積分値
∬KχAdxdy
を指す。
( reference )
・日本数学会編集『岩波数学辞典(第三版)』 岩波書店、1985年、202項積分法(pp.520-525)→リーマン積分、
・高木貞治『解析概論:改訂第3版』岩波書店、1983年、第8章91-92節(pp.326-334.)
・吹田・新保『理工系の微分積分学』学術図書出版社、1987年、第7章1節(II)-(III) (pp.191-196).
・杉浦光夫『解析入門I』東京大学出版会、1980年、IV章§8(pp.254-261.) §9(pp.261-264.)(2重積分についてというよりもn変数関数全般ののリーマン積分、面積というよりも体積、を論じている。)
・笠原皓司『微分積分学』サイエンス社、1974年、7.2節[2]定義7.1.7(p.259.)。
・黒田成俊『21世紀の数学1:微分積分』共立出版、2002年、第10章2節(pp. 352-359.)。連続関数に限定。
・小平邦彦『解析入門II』 (軽装版)岩波書店、2003年、第7章 d)矩形塊上の積分(pp.327-330.)。有限個の矩形の合併集合に限定。連続関数に限定.。なお、pp.348-9.の注意において、内面積・外面積・面積確定などを述べたうえで、このテキストでは矩形と矩形の合併集合に積分範囲を限定して論じている旨、明らかにされている。
・高橋一『経済学とファイナンスのための数学』新世社、1999年、第3章3.8節I(pp. 106-108)。
・Walter Rudin,Principles of Mathematical Analysis,Mcgraw-Hill,1953-1976.
=ウォ-ルタ-・ルディン『現代解析学』共立出版、1971年、第6章。
・高橋陽一郎『岩波講座現代数学への入門:微分と積分2』 岩波書店、1995年、5章2節(pp.138-146.):。このテキストは、リーマン積分とルベーク積分の間という特殊な立場を進んで行っている気がする。ついていってよいのかどうか。
・片山孝次『微分積分学』(現代数学レクチャーズB-8)、培風館、1980年、p.202.極めて簡潔な要約。
和達三樹『理工系の数学入門コース1:微分積分』岩波書店、1988年、pp.138-9. アイデアだけ。厳密な議論なし。
小形正男『理工系数学のキーポイント7:多変数の微分積分』岩波書店、1996、87-89. アイデアだけ。厳密な議論なし。
・志賀浩二『ルベーグ積分30講』朝倉書店、1990年、第4講ふつうの面積概念―ジョルダン測度―(pp.24-29)。
・Lang,Serge.Undergraduate Analysis(Undergraduate
Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg
Tokyo,1983,Chapter 19. Multiple Integrals. (pp.468-482.)。

