定義
・実行列の和A+Bは、
AとBの型が一致する場合に限り、
対応する成分の 「実数体Rに 定義されている和」を成分とする行列として定義される。
・つまり、A, Bともに m×n行 列であるならば、
A+B
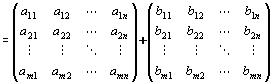
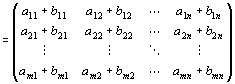
と定義される。
なお、aij,bijは実数で あり、
最終式の行列内の"+"は、実数体Rに 定義されている加法を指 す。
・上記定義を略記すると、 m×n行列A=(aij), B=(bij)にたいして、A+B =(aij+bij)
[文献]
『岩波数学辞典』83行列B (pp.219-220);
永田『理系のための線形代数の基礎』1.4(p.24);
斎藤『線形代数入門』2章§1(p.32);
藤原『線形代数』2.1(p.22)
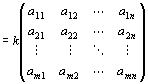
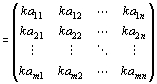
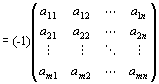
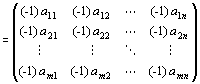 ∵
∵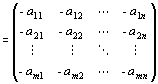
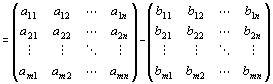
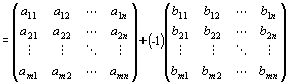
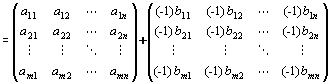 ∵行列の
∵行列の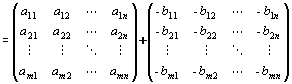
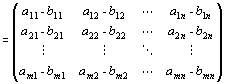 ∵
∵