計量実ベクトル空間に定義された内積の性質 ： トピック一覧
・定理：零ベクトルとの内積、スカラー倍したベクトルのそれ自身との内積、シュヴァルツの不等式、三角不等式
※計量実ベクトル空間関連ページ：ノルム・ノルム空間の定義/内積・計量実ベクトル空間の定義/正規直交系･正規直交基底の定義/直交系・直交基底と内積/直交系･正規直交系の性質/正規直交基底の存在と構成/計量同型写像/直交補空間
→線形代数目次・総目次
定理：零ベクトルとの内積は０
[砂田『行列と行列式』§7.1(a)定理7.9 (p.239);]
【舞台設定】
R：実数体R
V：実ベクトル空間
〈x,y〉：計量実ベクトル空間Vにおけるベクトルx,yの内積
【本題】
計量実ベクトル空間Vに属す任意のベクトルxと零ベクトルとの内積は０．
論理記号で表すと、∀x∈V（ 〈x,〇〉=〈〇,x〉=０）
※活用→同じベクトルどおしの内積の平方根はノルムの定義を満たす。
※なぜ？
・任意のx,y∈Vと任意の実数aにたいして、〈x,ay〉=a〈x,y〉 …(1)
∵内積であるための要件2：線形性2
・(1)について、任意の実数aを０とおくと、任意のx,y∈Vにたいして、〈x,０y〉=０〈x,y〉 …(2)
・任意のx,y∈Vにたいして、〈x,０y〉=〈x,〇〉 …(3)
∵ベクトルのスカラー０倍
・０〈x,y〉＝０ …(4)
・(3)(4)を(2)に代入して、
任意のx∈Vにたいして、〈x,〇〉=０
が得られる。ここから、内積であるための要件4：対称性を用いて、
任意のx∈Vにたいして、〈x,〇〉=〈〇,x〉=０
定理：線形性
[永田『理系のための線形代数の基礎』4.1問2(p.114);砂田『行列と行列式』§7.1(a)定理7.9 (pp.240-1);
志賀『ベクトル解析30講』第11講(p.79);]
【舞台設定】
R：実数体R
V：実ベクトル空間
〈x,y〉：計量実ベクトル空間Vにおけるベクトルx,yの内積
【本題】
計量実ベクトル空間Vに属す任意のベクトルxと任意の実数aに対して、
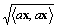
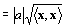
※活用→同じベクトルどおしの内積の平方根はノルムの定義を満たす。
※なぜ？
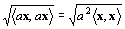∵内積であるための要件2：線形性2
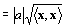∵絶対値の性質
シュヴァルツの不等式：
[斎藤『線形代数入門』４章§6計量線形空間(p.120);永田『理系のための線形代数の基礎』4.1(p.114);
砂田『行列と行列式』§7.1(a)定理7.9 (pp.240-1)志賀『ベクトル解析30講』第11講(pp.78-9);
志賀『固有値問題30講』8講(p.61);]
【舞台設定】
R：実数体R
V：実ベクトル空間
〈x,y〉：計量実ベクトル空間Vにおけるベクトルx,yの内積
【本題】
計量実ベクトル空間Vに属す任意のベクトルx,yについて、次の不等式が成立する。
｜〈x,y〉｜≦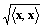
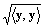
つまり、
ベクトルx,yの内積の絶対値は、「ベクトルxのノルム」と「ベクトルyのノルム」の積をこえない。
※なぜ？ [永田『理系のための線形代数の基礎』4.1(p.114);砂田『行列と行列式』§7.1(a)定理7.9 (pp.240-1)]
・xが零ベクトルであるときは、両辺０で成立。∵零ベクトルとの内積、内積の要件3：正値性
・以下、xが零ベクトルでないケースを考える。 …(1)
・任意の実数cにたいして、〈cx＋y, cx＋y〉≧０ …(2)
∵内積の要件3：正値性
・〈cx＋y, cx＋y〉
＝〈cx, cx＋y〉＋〈y, cx＋y〉 ∵内積の要件1：線形性1
＝〈cx, cx〉＋〈cx,y〉＋〈y, cx＋y〉 ∵内積の要件1：線形性1
＝〈cx, cx〉＋〈cx,y〉＋〈y, cx〉＋〈y, y〉 ∵内積の要件1：線形性1
＝〈cx, cx〉＋2〈cx,y〉＋〈y, y〉 ∵内積の要件4：対称性
＝c〈x, cx〉＋2〈cx,y〉＋〈y, y〉 ∵内積の要件2：線形性2
＝c2〈x, x〉＋2〈cx,y〉＋〈y, y〉 ∵内積の要件2：線形性2
＝c2〈x, x〉＋2c〈x,y〉＋〈y, y〉 ∵内積の要件2：線形性2
…(3)
・ここまで、cは、任意の実数とされていたのだから、
c=－〈x,y〉/〈x,x〉 とおいたところで、(2)（3）に変更はない。
(3)に、c=－〈x,y〉/〈x,x〉 を代入すると、
〈cx＋y, cx＋y〉＝〈x,y〉2 /〈x,x〉－2〈x,y〉2 /〈x,x〉＋〈y, y〉
＝（〈x,y〉2 －2〈x,y〉2）/〈x,x〉＋〈y, y〉
＝－〈x,y〉2/〈x,x〉＋〈y, y〉
これに(2)を適用して、
－〈x,y〉2/〈x,x〉＋〈y, y〉≧０
〈y, y〉≧〈x,y〉2/〈x,x〉 ∵両辺に〈x,y〉2/〈x,x〉を加える
〈x,x〉〈y, y〉≧〈x,y〉2 ∵両辺に〈x,x〉をかける
〈x,x〉〈y, y〉≧｜〈x,y〉｜2 ∵絶対値の性質
｜〈x,y〉｜2≦〈x,x〉〈y, y〉
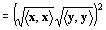
定理：三角不等式
[斎藤『線形代数入門』４章§6計量線形空間(p.120);永田『理系のための線形代数の基礎』4.1(p.114)
砂田『行列と行列式』§7.1(a)定理7.9 (pp.240-1);志賀『ベクトル解析30講』第11講(p.79);
志賀『固有値問題30講』8講(p.63);.]
【舞台設定】
R：実数体R
V：実ベクトル空間
〈x,y〉：計量実ベクトル空間Vにおけるベクトルx,yの内積
【本題】
計量実ベクトル空間Vに属す任意のベクトルx,yについて、次の不等式が成立する。
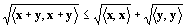
＊左辺の内積〈 , 〉内の＋はベクトル和、右辺の＋は実数の和。
つまり、
ベクトルx,yのベクトル和とそれ自身との内積の平方根は、
「ベクトルxとそれ自身のとの内積の平方根」と
「ベクトルyとそれ自身のとの内積の平方根」の和をこえない。
※活用→同じベクトルどおしの内積の平方根はノルムの定義を満たす。
※なぜ？
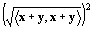
＝〈x＋y, x＋y〉
＝〈x, x＋y〉＋〈y, x＋y〉 ∵内積の要件1：線形性1
＝〈x, x〉＋〈x,y〉＋〈y, x＋y〉 ∵内積の要件1：線形性1
＝〈x, x〉＋〈x,y〉＋〈y, x〉＋〈y, y〉 ∵内積の要件1：線形性1
＝〈x, x〉＋2〈x,y〉＋〈y, y〉 ∵内積の要件4：対称性
≦〈x, x〉＋2｜〈x,y〉｜＋〈y, y〉 ∵絶対値の性質
≦〈x, x〉＋2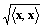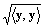＋〈y, y〉 ∵シュヴァルツの不等式
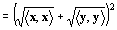
→[トピック一覧：内積の性質]
→線形代数目次・総目次
(reference)
線形代数のテキスト
ホフマン・クンツェ『線形代数学I』培風館、1976年。
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、4.1内積(p.114);。
佐武一郎『線形代数学(第44版)』裳華房、1987年、Ⅲベクトル空間§6ベクトル空間の公理化(p.117)。
志賀浩二『数学30講シリーズ：線形代数30講』朝倉書店、1988年。
藤原毅夫『理工系の基礎数学2：線形代数』岩波書店、1996年。
斎藤正彦『線形代数入門』東京大学出版会、1966年、４章§6計量線形空間(p.120)。
砂田利一『現代数学への入門：行列と行列式』2003年、§7.1-(a)内積 (pp.239-241).
解析学のテキスト
杉浦光夫『解析入門I』東京大学出版会、1987年、I章§4(pp.33-38)。
数理経済学のテキスト
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、§3.2.3(p.124)。
→[トピック一覧：内積の性質]
→線形代数目次・総目次