関数の左極限を単調増大列の収束へ言い換える定理
[加古『自然科学の基礎としての微積分』3.2節連続関数:定理3.1(注意)における示唆(p.31);伊藤『ルベーグ積分入門』定理4.2証明中の利用例.]
以下の命題Pと命題Qは互いに言い換え可能（つまりP⇔Q）。
命題P： x0におけるf(x)の左極限はA。
すなわち、f(x)→A ( x→x0−0)
命題Q：・ xn →x0 (n→∞) (つまり x0に収束する)
※x0は後出の数列 { xn }の第0項という意味ではないので注意
かつ、
・ x1＜x2＜x3＜…＜xn＜…＜x0 （つまり、狭義単調増加列で、任意のn∈N についてxn＜x0）
を満たす限りで任意につくった(どんな)数列{ xn }={ x1 , x2, x3,…}に対しても、
f (xn)→A (n→∞) (つまり数列 { f ( xn ) }={ f ( x1 ) , f ( x2 ), f ( x3 ),…}がAに収束する)
cf. 普通の極限/右極限の場合、
※利用例：関数の左連続性を単調増大列の収束へ言い換え、
[加古『自然科学の基礎としての微積分』3.2節連続関数:定理3.1(注意)における示唆(p.31);]
[証明：Ｐ⇒Ｑ]
命題P⇒関数の左極限の、数列の収束への言い換えの命題Q⇒ここで証明すべき定理の命題Q
[証明：Q⇒P]
仮定Q：・f (xn) →A（ n→∞ ） …(1)
ただし、数列 { xn }は、
xn→x0（ n→∞ ） …(2)
x1＜x2＜x3＜…＜xn＜…＜x0 …(3)
を満たす限りで任意の数列(をどのようにとってもよい)。
結論P： f (x)→A (x→x0−0) …(4)
（方針）：Q⇒Pを示すために、その対偶、すなわち「Pが不成立」⇒「Qが不成立」を示す。
結論P「(4): f (x)→A (x→x0−0)」が成り立たないなら、
仮定Q「(1): f (xn)→A（ n→∞ ）（{ xn }は、(2)(3)を満たす限りで任意の数列）」も成り立たない、
ことを示す。
本論：
(step1) 「Pが成り立たない」「(4)が成り立たない」という仮定の確認。[中内『ろんりの練習帳』118-122。]
「 (4): f (x)→A (x→x0−0)が成り立たない」と仮定する。
この仮定は、左極限の定義を用いて正確にとらえると、
任意の（どんな）正の実数ε0に対して（でも）、
「 −δ＜ x−x0 ＜0ならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ ( x0−δ, x0 )ならば、 f(x) ∈ ( A−ε0,A＋ε0) 」
を任意のxについて成り立たせる、ある正の実数δが存在するということ
の否定、すなわち、¬ ( ( ∀ε0 ＞0 ) ( ∃δ＞0 ) ( ∀x ) ( −δ< x−x0＜0 ⇒ | f (x)−A|＜ε0) ) となる。
＊ ＊ ＊
これは、
「 −δ＜ x−x0 ＜0ならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ ( x0−δ, x0 )ならば、 f(x) ∈ ( A−ε0,A＋ε0) 」
を任意のxについて成り立たせる、ある正の実数δが、
任意の（どんな）正の実数ε0に対して（でも）、存在するとは限らない
ということを意味するので、
「 −δ＜ x−x0 ＜0ならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ ( x0−δ, x0 ) ならば、 f(x) ∈ ( A−ε0,A＋ε0) 」
を任意のxについて成り立たせる正の実数δを存在させないような正の実数ε0が(少なくとは一つは)存在する
と書き換えられる。
厳密に言えば、前の論理式を、¬ ( ∀ A(x) x P(x) )と(∃A(x) x) (¬P(x) )が言い換え可能であることを用いて、
( ∃ε0＞0 ) ¬ ( ( ∃δ＞0 ) ( ∀x ) (−δ< x−x0＜0 ⇒ | f (x)−A|＜ε0 ) )
と書き換えられる、となる。
＊ ＊ ＊
「…を成り立たせる正の実数δを存在させない」というのは、「どんな風に正の実数δをとっても…を成り立たせない」といっても同じことなので、先の命題は、
「 −δ＜ x−x0 ＜0ならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ ( x0−δ, x0 )ならば、 f(x) ∈ ( A−ε0, A＋ε0) 」
を任意の(すべての)xについて成り立たせることを、
どんな風に正の実数δをとっても成り立たせない正の実数ε0が(少なくとは一つは)存在する」
と書き換えられる。
厳密に言えば、前の論理式を、¬ ( ∃A(x) x P(x) )と(∀A(x) x) (¬P(x) )が言い換え可能であることを用いて、
( ∃ε0 ＞0 ) ( ∀δ＞0 ) ¬ ( ( ∀x ) ( −δ< x−x0＜0 ⇒ | f (x)−A|＜ε0 ) )
と書き換えられる、となる。
＊ ＊ ＊
「『…を任意の（すべての）xについて成り立たせること』を成り立たせない」というのは、「…を成り立たせないxが少なくとも一つ存在する」といっても同じことなので、先の命題は、
「 −δ＜ x−x0 ＜0ならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ ( x0−δ, x0 )ならば、 f(x) ∈ ( A−ε0, A＋ε0) 」
を成り立たせないxを、どんな風に正の実数δをとろうが、少なくとも一つ存在させる
正の実数ε0が(少なくとは一つは)存在する」
と書き換えられる。
厳密に言えば、前の論理式を、¬ ( ∀ A(x) x P(x) )と(∃A(x) x) (¬P(x) )が言い換え可能であることを用いて、
( ∃ε0＞0 ) ( ∀δ＞0 ) ( ∃ x ) ¬ ( −δ< x−x0＜0 ⇒ | f (x)−A|＜ε0 )
と書き換えられる、となる。
＊ ＊ ＊
「 −δ＜ x−x0 ＜0ならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ ( x0−δ, x0 )ならば、 f(x) ∈ ( A−ε0,A＋ε0) 」
を成り立たせない、とは、
「 −δ＜ x−x0 ＜0なのに | f(x)−A|＜ε0 でない」
すなわち「 x∈ ( x0−δ, x0 )なのに f(x) ∈ ( A−ε0,A＋ε0) でない」
という命題が成立することであるから、
先の命題は、
「 −δ＜ x−x0 ＜0なのに、 | f(x)−A|＜ε0 でない」
すなわち「 x∈ ( x0−δ, x0 ) なのに、 f(x) ∈ ( A−ε0, A＋ε0) でない」
を成り立たせるxを、どんな風に正の実数δをとろうが、少なくとも一つ存在させる
正の実数ε0が(少なくとは一つは)存在する
と書き換えられる。
厳密に言えば、前の論理式を、¬(A⇒B)とA∧¬(B)が書き換え可能であることを用いて、
( ∃ε0＞0 ) ( ∀δ＞0 ) ( ∃ x ) ( −δ< x−x0＜0 かつ ¬( | f (x)−A|＜ε0 ) )
と書き換えられる、となる。
＊ ＊ ＊
「 | f(x)−A|＜ε0 でない」すなわち「f(x) ∈ ( A−ε0,A＋ε0) でない」は、もちろん、
「 | f(x)−A|≧ε0 である」すなわち「f(x)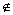 
( A−ε0,A＋ε0) 」 のことだから、
先の命題は、
「 −δ＜ x−x0 ＜0なのに、 | f(x)−A|≧ε0 」
すなわち「 x∈ ( x0−δ, x0 )なのに、 f(x) 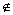( A−ε0,A＋ε0) 」
を成り立たせるxを、どんな風に正の実数δをとろうが、少なくとも一つ存在させる
正の実数ε0が(少なくとは一つは)存在する」
と書き換えられる。
厳密に言えば、
( ∃ε0＞0 ) ( ∀δ＞0 ) ( ∃ x ) (−δ< x−x0＜0 かつ ( | f (x)−A|≧ε0 ) ) …(5)
＊ ＊ ＊
先の命題は、
| f(x)−A|≧ε0 すなわち f(x) 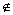( A−ε0,A＋ε0)
を成り立たせるx∈( x0−δ, x0 )を、どんな風に正の実数δをとろうが、少なくとも一つ存在させる
正の実数ε0が(少なくとは一つは)存在する
と書き換えられる。
厳密に言えば、前の論理式を、( ∃A(x) x ) P(x)と∃x ( A(x) ∧ P(x) )が書き換え可能であることを用いて、
( ∃ε0＞0 ) ( ∀δ＞0 ) ( ∃ x∈( x0−δ, x0 ) ) (| f (x)−A|≧ε0)
と書き換えられる、となる。
これは、
δを調整して( x0−δ, x0 )をどうとっても、
( A−ε0 , A＋ε0)の範囲からf(x)を飛び出させるx∈( x0−δ, x0 )を少なくとも一つ存在させるε0が存在する
ことを、意味している。
以上、「P『(4): f (x)→A (x→x0−0)』が成り立たない」という仮定の正確な意味を書き下していった。
(step2-1) 「Pが成り立たない」「(4)が成り立たない」という仮定のもとで、ある数列が存在する。
「Pが成り立たない」「(4)が成り立たない」という仮定は、(5)で示したように、
ε0をうまく選べば、「−δ< x−x0＜0 かつ | f (x)−A|≧ε0 」を満たすxが、その具体的な値などは不明であるもののとにかく、δをどんな正数にしようとも、確かに存在することを意味していた。
すると、このε0のもとで、「−δ< x−x0＜0 かつ | f (x)−A|≧ε0」を満たすxばかりをあつめて並べた数列というのも、δ>0が何であれ、存在することになる。
δはどんな正数でもよいというのだから、たとえば、δ=1/n(nは1以上の自然数)としても、このことは成り立つ。
つまり、
(5)が存在を保証する一定の正数ε0のもとで、
各自然数n≧1に対して、
「−1/n ＜ xn−x0＜0」すなわち「xn ∈ ( x0−1/n, x0 )」を満たし、…(6)
かつ
「| f(xn)−A|≧ε0」すなわち「f(xn ) 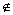( A−ε0 , A＋ε0)」を満たす …(7)
ようなxnが存在する。
厳密にいえば、「(4)が成り立たない」という仮定のもとでは、(5)はδ>0を任意として成立するのだから、
(5)にδ=1/n(自然数n≧1)を入れて、
( ∃ε0＞0 ) ( ∃ xn ) ( −1/n < xn−x0＜0かつ ( | f (xn)−A|≧ε0 ) )
すなわち、 ( ∃ε0＞0 ) ( ∃ xn ∈( x0−1/n, x0 ) ) (| f (xn)−A|≧ε0)
としても「(4)が成り立たない」という仮定のもとで成り立つことになる
だから、(5)が存在を保証する一定の正数ε0のもとで、(6) (7)を満たすxnを選んできて、
それを、x1, x2,…xn,…というように並べてつくった数列 { xn }というのも存在することになる。
なお、数列 { xn } は(6)を満たすことから、
xn→x0（ n→∞ ） かつ 任意のn∈N についてxn＜x0 …(6')
も満たすことを、ここで確認しておく。
(step2-2) 「Pが成り立たない」「(4)が成り立たない」という仮定のもとで、ある単調増大列が存在する。
上記の数列 { xn }は、単調増大列とは限らない。
たとえば、x1= x0−0.1, x2= x0−0.4 で、x1＞ x2 となるような数列 { xn }も、
(7)についてはともかくとして、(6)は満たす。
ここでは、上記の数列 { xn }から、下記の選別ルールにしたがって、一定の項を排除し、一定の項を残すことで、単調増大列となる部分列{λm}を作る。
（選別のルール）
・nよりも小さな任意の自然数kに対して、xk＜xnを満たす
(つまり、xnがxn-1, xn-2,…, x3, x2, x1より大きい)
数列 { xn }の項だけを残し、
・nよりも小さな任意の自然数kに対して、xk＜xnを満たさない
(つまり、xnがxn-1, xn-2,…, x3, x2, x1よりも小さいか、等しい)
数列 { xn }の項を排除する。
ここで、数列{λm}の性質を確認しておく。
・λm →x0（ n→∞ ）…(8)
なぜかというと、
(6')より、数列 { xn }はx0に収束する。
収束する数列の任意の部分列は収束するから、
数列 { xn }の部分列である{λm}もx0に収束する。
・λ1＜λ2＜λ3＜…＜λn＜…＜x0 …(9)
なぜかというと、
(6')より、任意のn∈N についてxn＜x0
ここから、上記のルールで選別して、単調増大列となるから、
(9)がえられる。
・(5)が存在を保証する一定の正数ε0のもとで、全てのmに対して、f (λm)は、
「| f (λm)−A|≧ε0」すなわち「f (λm ) 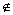( A−ε0 , A＋ε0)」を満たす …(10)
なぜかというと、
数列{λm}の全ての項は、もともと数列{ xn }の項。
そして、数列{ xn }の項はすべて(7)を満たす（というか、(7)を満たすものだけを選んだのが{ xn }）
だから、数列{λm}の全ての項は、(7)を満たす。
(step3) 「Pが成り立たない」「(4)が成り立たない」という仮定のもとで存在する「ある単調増大列」が「Qが成り立たない」ことを証明する。
(5)が存在を保証する一定の正数ε0のもとで(6) (7)を満たすxnを並べた数列 { xn }から、
step2-3でつくった部分列{λm}は、(8)より(2) を(9)より(3)を満たしている。
しかし、そのfによる像 f (λ1), f (λ2),…を並べた数列{ f (λm) }は(10)より
(1): f (λm)→A（ n→∞ ）
すなわち、任意の正の実数εに対して、
「 n≧Nならば、 | f (λm) −A |＜ε 」
を成り立たたせるある自然数Nが存在する
を満たさない。数列{ f (λm) }は、(5)が存在を保証する一定の正数ε0のもとで| f (xn) −A |≧εとなるxnをわざわざ選んできて並べた数列の部分列なのだから。
＊ ＊ ＊
Qは、(2)(3)を満たす全ての数列に対して(1)が成立することを主張する命題であるから、
(2)(3)を満たすのに(1)が成立しないという反例が一つでもあれば、否定される。
(5)が存在を保証する一定の正数ε0と、
そのε0のもとで(6) (7)を満たすx1, x2,…xn,…を並べた数列 { xn }の部分列{λm}の存在は、そのような反例となる。
＊ ＊ ＊
以上から、Q⇒Pの対偶、すなわち、
結論P「(4): f(x)→A (x→x0−0)」が成り立たないなら、
仮定Q「(1): f (xn)→A（ n→∞ ）（{ xn }は、(2)(3)を満たす限りで任意の数列）」も成り立たない、
が示された。
ゆえに、Q⇒P、すなわち、
仮定Q「(1): f (xn)→A（ n→∞ ）（{ xn }は、(2)(3)を満たす限りで任意の数列）」が成り立てば、
結論P「(4): f(x)→A (x→x0−0)」も成り立つ、
が示されたことになる。