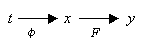��`�F���n���@primitive function
�@��f(x)�ɑ��āAF'(x)=f(x)������F(x)���A�܂�A����������f(x)�ł����F(x)���A
�@f(x)�����n���ƌĂсA�ȉ��̋L���ŕ\���B
�@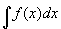
�@�Ȃ��A���̋L���́Af(x)�̌��n���S�̂��w���Ă���[�a�B�w�����ϕ��x79;]�B
�@���X�̌��n���Ɛϕ��萔�@
�����̌��n����s��ϕ��ƌĂԂ��Ƃ����邪�A�u�s��ϕ��v�Ȃ�p��̒�`�͓��ꂳ��Ă��Ȃ��B
�@���������āA�u�s��ϕ��v�Ȃ�p���p����ꍇ�ɂ́A���ꂪ��
���w���Ă���̂����A
�@���̓s�x�A�����肩��ǂݎ�ɑ��āA�܂т炩�ɂ��Ă����K�v������B
�@���̂�����̎���ɂ��ẮA�����w��͓���I�xp.165������B
���܂�A���n���́A�����̋t�Z�Ƃ��Ē�`�����B
�@�����A(��)�ϕ��́A�����Ƃ͖��W�ɒ�`�t����ꂽ��ŁA
�@��͊w�̊�{�藝�ɂ���ď��߂āA�����̋t�Z=���n���ƌ��ѕt�����邱�Ƃɒ��ӁB
�i���L�@�j
��1dx����dx�A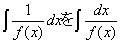 �@
�@
�@�@�@�@�@�ȂǂƁA���L����B[���c�V�ہw���H�n�̔����ϕ��w�x75;]
�y�����z
�@�E���c�V�ہw���H�n�̔����ϕ��w�x73�G75;
�@�E�����w��͓���I�x164
�@�E�a�B�w�����ϕ��x79
�藝�Ff(x)�̌��n���ǂ����̊W�Ɛϕ��萔
�@�@�@�@
�@F(x)��f(x)�����I�ɂ����������n���Ƃ���ƁA
�@f(x)�����I�ɂ�����S�Ă����n���́AC��萔�Ƃ��āA
�@�@�@F(x)�{C
�@�̌`�ŕ\�����B
�@�萔C���ϕ��萔 integral constant; constant of integration�ƌĂԁB
(�ؖ�)
F(x),G(x)���A���ꂼ��A���I�ɂ�����f(x)�����n���̈�ł���Ƃ���B�c����@
���I�ɂ����āA
( G(x)�|F(x) )'=G'(x)�|F'(x)�@�����̘a���̔���
�@�@�@�@�@= f(x)�|f(x)�@�@�@�扼��@
�@�@�@�@�@=0
�܂�A��G(x)�|F(x)�������́A���I�ɂ����ď�Ƀ[���ƂȂ邩��A
���ϒl�藝�̌n���AG(x)�|F(x)�����I��Œ萔�ł���B
���̒萔��C�Ƃ����A
�@G(x)�|F(x)=C
�@��G(x) =F(x)�{C
�@
�y�����z
�@�E�g�c�I�c�˓c�w��b��́x129;
�@�E���c��w�Љ�Ȋw�҂̂��߂̊�b���w�x98;
�@�E���c�V�ہw���H�n�̔����ϕ��w�x73;
�@�E�a�B�w�����ϕ��x78-9;
�@�E�����w��͓���I�x164]
�藝�F��F'(x) dx=F(x)+C�@�@
�@�E[�{�w�����Ɛϕ�1�x109;
�@�E �a�B�w�����ϕ��x79.]
�藝�F���`��
[���c��w�Љ�Ȋw�҂̂��߂̊�b���w�x99; �{�w�����Ɛϕ�1�x109-110; �a�B�w�����ϕ��x78-87.]
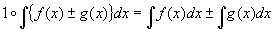
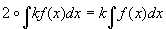
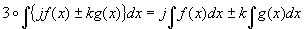
f(x)�����n��(�̑S��)��F(x) �Ag(x)�����n��(�̑S��)��G(x)�Ƃ����B
���n���̒�`�ƋL�@���A���̂��Ƃ͈ȉ��̓�ʂ�ɕ\�����邱�Ƃ��ł���B
�@F'(x)=f(x)�A�@G'(x)=g(x)�@�@�@�@�@�@�@�c�@�@
�@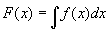 �A
�A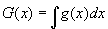 �@�c�A
�@�c�A
(1�ւ̏ؖ�)
{F(x)�}G(x)}'=F'(x)�}G'(x)�@�@�����̘a���̔�������
�@�@�@�@�@�@= f(x)�}g(x)�@�@��@
���ܓ���ꂽ���@{F(x)�}G(x)}'= f(x)�}g(x)�@�́A���n���̒�`�ƋL�@���A
�uF(x)�}G(x)��f(x)�}g(x)�����n��(�̑S��)�ł���v�ƕ\���ł��A�ȉ��̋L���ŕ\����B
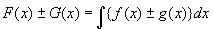
�A�ō��ӂ�����������ƁA
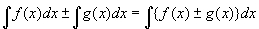 �@�@
�@�@
�@ (�ؖ��I���)
(2�ւ̏ؖ�)
{ k F (x) } '= k F ' (x) �@�@�����̒萔�{�̔�������
�@�@�@�@�@= k f(x)�@�@��@�@
���ܓ���ꂽ���@{ k F (x) }'= k f(x)�@�́A���n���̒�`�ƋL�@���A
�uk F (x)��k f(x)�����n���ł���v�ƕ\���ł��A�ȉ��̋L���ŕ\����B
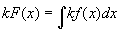 �@
�@
�A�ō��ӂ�����������ƁA
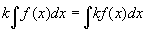 �@�@
�@�@
�@ (�ؖ��I���)
(3�ւ̏ؖ�)
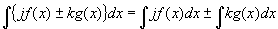 �@�@���̒藝1���
�@�@���̒藝1���
�@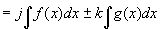 �@�@���̒藝2���
�@�@���̒藝2���
�@(�ؖ��I���)
�@
�藝�F�����ϕ��@ integration by parts
�@�@�@�@[���c��w�Љ�Ȋw�҂̂��߂̊�b���w�x103;�{�w�����Ɛϕ�1�x115-7; �a�B�w�����ϕ��x83-4;
�@�@�@�@���c�V�ہw���H�n�̔����ϕ��w�x74; ������w�o�ϊw�ƃt�@�C�i���X�̂��߂̐��w�x87;
�@�@�@�@�����w��͓���I�x170.]
�@��f(x)g'(x)dx=f(x)g(x)�|��f' (x)g (x)dx
(�K�p��)��log |x| dx�̌v�Z �A
(�ؖ�)�@���̐ς̔������������n���̌�@�Ō��������������B
���̐ς̔����������A{ f (x) g (x) }'= f ' (x) g (x) �{ f (x) g ' (x)�@
���̎��́A���n���̒�`�ƋL�@�ɏ]���A
�uf (x) g (x) �� f '(x)g(x)�{f(x)g '(x)�����n���ł���v�ƕ\���ł��A�ȉ��̋L���ŕ\����B
�@��{ f ' (x) g (x) �{ f (x) g ' (x) }dx = f (x) g (x)
���n���̐��`�����A����́A�ȉ��̂悤�ɏ����Ȃ�����B
�@��f '(x)g(x)dx +��f(x)g '(x)dx = f (x) g (x)
���ӑ�1�����E�ӂֈڍ�����A
�@��f(x)g'(x)dx = f(x)g(x)�|��f' (x)g (x)dx
�@ (�ؖ��I���)
�@
�藝�F�u���ϕ��@ integration by substitution(�ϕ��̕ϐ��ϊ�����)
�@�@�@�@[�g�c�I�c�˓c�w�����E�ϕ��x110-1.���c��w�Љ�Ȋw�҂̂��߂̊�b���w�x101-3;
�@�@�@�@�{�w�����Ɛϕ�1�x111-5; �a�B�w�����ϕ��x81-3; ���c�V�ہw���H�n�̔����ϕ��w�x74;
�@�@�@�@�����w�o�ϊw�ƃt�@�C�i���X�̂��߂̐��w�x80.]
��(t)��t�������\�����Ƃ���Bx=��(t)�Ƃ����A
�ȉ��̂悤�ɁAx�̊���x�ɂ��Ă̌��n���́At�̊���t�ɂ��Ă̌��n���ɕϊ������B
�@��f(x)dx=��f(��(t))��' (t)dt
(�o����) �@���ӂ�f(x)��x��x=��(t)�����A���ӂ�dx�� dx =(dx /dt)�Edt=��' (t)dt�����B
�@�@�@�@�@����ƁA�E�ӂɂȂ�B
(�ؖ�)�@�������̔������������n���̌�@�Ō��������B
�ݒ�F
��̊�y=F(x) =��f(x) dx�@�Ɓ@x=��(t)�@������Ƃ���B�c�@
����ƁA���n���̒�`�ƋL�@�ɂ��Ay=F(x)�́Ax�ɂ��Ă������́A
�@�@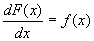 �@�@�@�c�A
�@�@�@�c�A
�ƂȂ�B
�����Ax=��(t)�������\�����ł���Ƃ��A
����t�ɂ��Ă��������A��' (t)�ŕ\�����Ƃɂ���B�c�B
���āA���̂悤�ȓ�̊�y=F(x) =��f(x) dx��x=��(t)�Ƃ�������y=F(��(t))���l����B�c�C
�@�@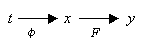
�{��F
�C�ł�����������y=F(��(t))��t�����������B
�������̔�������:dy/dt = dy/dx�Edx/dt���A
�@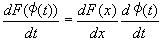
�@�@�@�A�B��p���ĉE�ӂ�ό`���āA
�@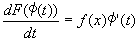
�@�@�@�@�@�@= f (��(t)) ��' (t)�@��@��x=��(t)�Ɛݒ肵������B�@
���̎��́A���n���̒�`�ƋL�@�ɏ]���A
�uF(��(t))��f(��(t))��' (t)��t�ɂ��Ă����n���ł���v�ƕ\���ł��A�ȉ��̋L���ŕ\����B
�@F(��(t)) =��{ f(��(t))��' (t) }dt
�@���̍���F(��(t))�́AF(��(t))=F(x)�@�@��@��x=��(t)�Ɛݒ�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@=��f(x) dx�@��@��=F(x) =��f(x) dx�Ɛݒ�
�@������A��������ӂɓ���āA�@
�@��f(x) dx=��{ f(��(t))��' (t) }dt
�@�@�@ (�ؖ��I���)
(��̗�)
a,b,n�����R���̒萔�Ƃ���B
x�̊���x�ɂ��Ă����n��(�̑S��)��(ax+b)n dx�@���A
t=ax+b ���Ȃ킿x=��(t)=(t�|b)/a��t/a�|b/a�Ƃ����āA
t�̊���t�ɂ��Ă����n��(�̑S��)�ɒu��������ƁA
��(ax+b)n dx=��(t n/a)dt
�ݒ�F
��(�̃O���[�v)y= F(x) =��(ax+b)ndx�@��x=��(t)= t/a�|b/a������Ƃ��āA
����������(�̃O���[�v)y=F(��(t))���l����B �@�c�@
�Ȃ��A���n���̒�`�ƋL�@����Ay=F(x)�́Ax�ɂ��Ă�������f(x)=(ax+b)n=tn�ł���B���Ȃ킿�A
�@�@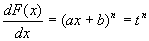 �@�@�@�c�A
�@�@�@�c�A
�{��F
�@��������(�̃O���[�v)y=F(��(t))��t�����������B�@
�������̔�������:dy/dt = dy/dx�Edx/dt���A
�@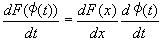
�A��p���ĉE�ӂ�ό`���āA
�@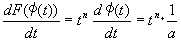
���̎��́A���n���̒�`�ƋL�@�ɏ]���A
�uF(��(t))�� tn/ a��t�ɂ��Ă����n��(�̑S��)�ł���v�ƕ\���ł��A�ȉ��̋L���ŕ\����B
F(��(t)) = �� tn/ a dt
�@�@���̍��ӂɂ��āA
�@�@F(��(t))=F(x)�@�@�@��x=��(t)�Ɛݒ�
�@�@�@�@�@=��(ax+b)n dx�@�@��F(x) =��(ax+b)ndx�@�Ɛݒ�
�@�@������A
�@��(ax+b)n dx= �� tn/ a dt�@�@
�@
��{�I�Ȋ��̌��n��
[�g�c�I�c�˓c�w�����E�ϕ��x105-9;���c��w�Љ�Ȋw�҂̂��߂̊�b���w�x99;�{�w�����Ɛϕ�1�x110-7; �a�B�w�����ϕ��x79-84; ���c�V�ہw���H�n�̔����ϕ��w�x74-5; �����w�o�ϊw�ƃt�@�C�i���X�̂��߂̐��w�x84-5.]
�E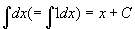 �@�@[�a�B�w�����ϕ��x79.]
�@�@[�a�B�w�����ϕ��x79.]
�i�Ȃ��H�j
�@�@���n���̒�`�ƋL�@���A���ӂ̌��n���́A����������1�ƂȂ�x�̊��̑S�̂��w���Ă���B
�@�@F(x)=x�̓����́AF'(x)=1�ƂȂ邩��(��)�AF(x)=x�́A���ӂ��w�����n���̂����̈���ł���B
�@�@�藝���A��̌��n����F(x) =x�Ȃ�A
�@�@���̑S�Ă̌��n���́A�C�ӂ̒萔��C�Ƃ��āAF(x)+C=x+C�ŕ\���邩��A
�@�@��dx= x+C�@
�E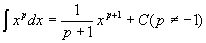
��p�������łȂ��ꍇ��x>0�Ƃ���[���c��w�Љ�Ȋw�҂̂��߂̊�b���w�x99]
�i�Ȃ��H�j
�@(i) p�������ł���ꍇ
�@�@���n���̒�`�ƋL�@���A���ӂ̌��n���́A����������x p �ƂȂ�x�̊��̑S�̂��w���Ă���B
�@�@F(x)= x p+1/(p+1)�̓����́AF'(x)= x p�ƂȂ邩��(��)�A
�@�@F(x)= x p+1/(p+1)�́A���ӂ��w�����n���̂����̈���ł���B
�@�@�藝���A��̌��n����F(x) = x p+1/(p+1)�Ȃ�A
�@�@���̑S�Ă̌��n���́A�C�ӂ̒萔��C�Ƃ��āAF(x)+C�ŕ\���邩��A
�@�@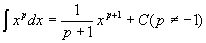 �@
�@
�@(ii) p�������łȂ��ꍇ(x>0�Ƃ���)
�@�@���n���̒�`�ƋL�@���A���ӂ̌��n���́A����������x p �ƂȂ�x�̊��̑S�̂��w���Ă���B
�@�@F(x)= x p+1/(p+1)�̓����́AF'(x)= x p�ƂȂ邩��(��)�A
�@�@F(x)= x p+1/(p+1)�́A���ӂ��w�����n���̂����̈���ł���B
�@�@�藝���A��̌��n����F(x) = x p+1/(p+1)�Ȃ�A
�@�@���̑S�Ă̌��n���́A�C�ӂ̒萔��C�Ƃ��āAF(x)+C�ŕ\���邩��A
�@�@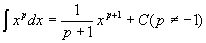 �@
�@
�@
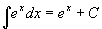
�i�Ȃ��H�j
�@�@���n���̒�`�ƋL�@���A���ӂ̌��n���́A����������e x�ƂȂ�x�̊��̑S�̂��w���Ă���B
�@�@F(x)= e x�̓����́AF'(x)= e x�ƂȂ邩��(��)�AF(x)= e x �́A���ӂ��w�����n���̂����̈���ł���B
�@�@�藝���A��̌��n����F(x)= e x�Ȃ�A
�@�@���̑S�Ă̌��n���́A�C�ӂ̒萔��C�Ƃ��āAF(x)+C= F(x)= e x +C�ŕ\���邩��A
�@�@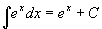
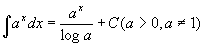
�i�Ȃ��H�j
�@�@���n���̒�`�ƋL�@���A���ӂ̌��n���́A����������a x�ƂȂ�x�̊��̑S�̂��w���Ă���B
�@�@F(x)= a x/log a��x�ɂ��Ă̓����́A
�@�@�@F'(x)= (1/log a) (a x)'�@�@��(1/log a)�͒萔������A���̒萔�{�̔�����������B
�@�@�@�@�@= (1/log a) (a x log a)�@ (��)
�@�@�@�@�@= a x�@
�@�@�ƂȂ邩��@
�@�@F(x)= a x/log a�́A���ӂ��w�����n���̂����̈���ł���B
�@�@�藝���A��̌��n����F(x)= a x/log a�Ȃ�A
�@�@���̑S�Ă̌��n���́A�C�ӂ̒萔��C�Ƃ��āAF(x)+C= a x/log a +C�ŕ\���邩��A
�@�@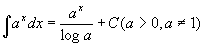
[���c�V�ہw���H�n�̔����ϕ��w�x75; ���c��w�Љ�Ȋw�҂̂��߂̊�b���w�x103; �a�B�w�����ϕ��x83-84;]
�i�Ȃ��H�j���j�F�����ϕ��@:��f(x)g'(x)dx=f(x)g(x)�|��f' (x)g (x)dx ��f(x)=log|x|, g(x)=x�Ƃ��ēK�p
�@f(x)=log|x|�Ƃ���ƁAf '(x)=1/x (��)�Ag(x)=x�Ƃ���ƁAg'(x)=1������A
�@f(x)=log|x|, g(x)=x�Ƃ��������ϕ��@�̓����́A
�@��log|x|dx=log|x|�Ex�|��dx�@
�@�@�@�@�@�@= xlog|x|�|x�|C�@�@�@��1�̌��n���@
�@��t=ax+b�Ɩ߂�
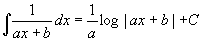
�i�Ȃ��H�j
�@x�̊���x�ɂ��Ă����n��(�̑S��)��(ax+b)�|1 dx�@���A
�@t=ax+b ���Ȃ킿x=��(t)=(t�|b)/a��t/a�|b/a�Ƃ����āA�u�����ϕ��̌�����p���āA
�@t�̊���t�ɂ��Ă����n��(�̑S��)�ɒu��������ƁA
�@��(ax+b) �|1 dx=��(t �|1/a)dt�@���u���ϕ��̋�̗��̐���������B
�@�@�@�@�@�@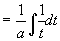 �@�@�@�@��
�@�@�@�@��
�@�@�@�@�@�@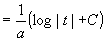 �@��
�@��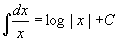
�@�@�@�@�@�@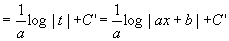
�@��t=ax+b�Ɩ߂�
�E��ʂɁ@��f(x) dx= F(x)+C�Ȃ�A
�@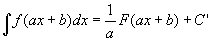 �@�@[�a�B�w�����ϕ��x83]
�@�@[�a�B�w�����ϕ��x83]
�i�Ȃ��H�j
step1:
�@x�̊���x�ɂ��Ă����n��(�̑S��)��f(ax+b) dx�@���A
�@t=ax+b ���Ȃ킿x=��(t)=(t�|b)/a��t/a�|b/a�Ƃ����āA�u�����ϕ��̌�����p���āA
�@t�̊���t�ɂ��Ă����n��(�̑S��)�ɒu��������ƁA
�@�@��(ax+b) dx= (1/a)��f(t) dt
�@���̉ߒ����ڂ����ǂ��ƁA�ȉ��̂悤�ɂȂ�B
�@�ݒ�F
�@��(�̃O���[�v)y= G(x) =��f(ax+b)dx�@��x=��(t)= t/a�|b/a(���Ȃ킿t=ax+b)������Ƃ��āA
�@����������(�̃O���[�v)y=G(��(t)) =��f(a��(t)+b)dx=��f(t)dx�@���l����B �@�c�@
�@�Ȃ��A���n���̒�`�ƋL�@����Ay=G(x)�́Ax�ɂ��Ă�������g(x)= f(ax+b) = f(t)�ł���B���Ȃ킿�A
�@�@�@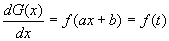 �@�@�@�c�A
�@�@�@�c�A
�@�{��F
�@�@��������(�̃O���[�v)y=G(��(t))��t�����������B
�@�������̔�������:dy/dt = dy/dx�Edx/dt���A
�@�@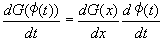
�@�A��p���ĉE�ӂ�ό`���āA
�@�@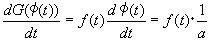
�@���̎��́A���n���̒�`�ƋL�@�ɏ]���A
�@�uG(��(t))�� f(t)/ a��t�ɂ��Ă����n��(�̑S��)�ł���v�ƕ\���ł��A�ȉ��̋L���ŕ\����B
�@G(��(t)) = �� f(t)/ a dt
�@�@�@�@�@= (1/a)��f(t) dt�@�@��
�@�@�@���̍��ӂɂ��āA
�@�@�@�@G(��(t))=G(x)�@�@�@��x=��(t)�Ƃ��łɐݒ肳��Ă���
�@�@�@�@�@�@�@�@=��f(ax+b)dx�@ ��G(x) =��(ax+b)ndx�@�Ƃ��łɐݒ肳��Ă���
�@������A
�@��(ax+b) dx= (1/a)��f(t) dt
step2:
�@����āA��f(x) dx= F(x)+C�Ȃ�A
�@��(ax+b) dx= (1/a)��f(t) dt=(1/a)(F(t)+C)
�@�@�@�@�@�@=(1/a)(F(ax+b)+C)�@�@��t=ax+b�Ɩ߂�
�@�@�@�@�@�@ =(1/a)F(ax+b)+(1/a)C
�@
�Z�p�F�L�����̌��n���|�������������@�@
�L�����̌��n���͕K�����߂���B
�y�����z
�@�E���c��w�Љ�Ȋw�҂̂��߂̊�b���w�x104-5
�@�E���c�V�ہw���H�n�̔����ϕ��w�x78-80
�@�E�a�B�w�����ϕ��x84-7.
�ireference�j
���{���w��ҏW�w��g���w���T�i��O�Łj�x��g���X�A1985�N�A202���ϕ��@(pp.520-525).
�g�c�k��E�I�c���E�˓c�G�w���a63�N3/31�����Ȍ���ύ����w�Z���w�ȗp�@�����w�Z�@��b��́@�V���Łx�[�ъفApp.128-133.
�g�c�k��E�I�c���E�˓c�G�w�������N3/31�����Ȍ���ύ����w�Z���w�ȗp�@�����w�Z�@�����E�ϕ��@�V���Łx�[�ъفApp.104-14.
���c�E�V�ہw���H�n�̔����ϕ��w�x�w�p�}���o�ŎЁA1987�N�BPp.73-83.
������w�o�ϊw�ƃt�@�C�i���X�̂��߂̐��w�x�V���ЁA1999�N�App.82-85.
�����M�F�w��͓���I�x (�y����)��g���X�A2003�N p.164.
���Y���v�w��͓���I�x��g���X�A1980�N�App.229-247:1�ϐ����̐ϕ��ɓ���Ȑ����i���n���A�c�j�B
���ؒ厡�w��͊T�_�@������O���x��g���X�A1983�N�App.89-90; 100-102;111:��ϕ��̒u���ϕ��@.
�{�a�F�w��g�u�����㐔�w�ւ̓���F�����Ɛϕ�1�x��g���X�A1995�N�A107-117.
��쌒���Y�E�c��ÍG�w�Љ�Ȋw�҂̂��߂̊�b���w�@�������x�։ؖ[�App.98-105.
�a�B�O���w���H�n�̐��w����R�[�X�P:�����ϕ��x��g���X�A1988�N�App.78-87.
�_�J�a��E�Y�䌛�w�o�ϊw�̂��߂̐��w�����x������w�o�ʼn�A1996�N�App.331:��`;p. 332-334.
�@