定義：《実数の集合》の内点　inner point


→ビギナー向け「内点」定義　

→厳密な「内点」定義：

　　→　距離のみを用いた表現
　　→　開区間を用いた表現
　　→　近傍を用いた表現

　【一般化】
　　→R2における集合の内点 / Rnにおける集合の内点
　　→距離空間一般における集合の内点

→実数－《実数の集合》間の位置関係一覧
→トピック一覧：距離空間(R,d)
→総目次　

【ビギナー向け】　きわめて感覚的な「内点」定義

・「実数aが『《実数の集合E》の内点』である」とは、

　　　【条件1】　実数a自体が「Eに属す実数」であって、
　　　なおかつ　
　　　【条件2】　実数aの両隣（直前・直後の両方）も、「Eに属す実数」である　
　　　　　　　（実数aは、「Eに属す実数」に両隣から挟まれている）

　ということ。

・内点感覚が馴染んだところで、下記《厳密な「内点」定義》への即時アップグレード推奨。
　この定義には、決定的な不備があるので[下欄]。。


【一般化】　R2における内点/Rnにおける内点/距離空間一般における内点
【性質】　・「Aの内点」は、すべて、Aに属す。[小平『解析入門I』§1.6-b(p.56):R2]　　
　　　　・int A⊂A⊂Aの閉包 　　[de la Fuente：2.4(a)(p.60);松坂『解析入門3』12.1-C(p.52;53)]
　　　　→内点・外点・境界点の関係　

　　　　→触点と内点・外点・境界点との関係　
　　　　→内点・外点・境界点と集積点との関係

　





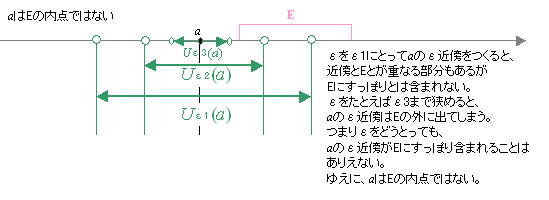
【上記の「内点」定義の曖昧さ】

　・自然数や整数のなかで考えるときは、自然数nの「直前」「直後」「両隣」は、ハッキリしている。
　　たとえば、「3の直前」は2、「3の直後」は4、したがって、「3の両隣」は2と4、というように。

　・ところが、実数の範囲に広げて考えると、
　　　実数aの「直前」「直後」「両隣」は、何を指すのか、不明確になってしまう。　

　・たとえば、πの「直前」「直後」「両隣」とは、何を指すのだろう？　
　　　　　・3は、πの「前」にはあるけれど、
　　　　　　　　　3よりは、3.1のほうが、πの「直前」には相応しい。
　　　　　・しかし、3.1よりは、3.14のほうが、πの「直前」には相応しい。
　　　　　・しかし、3.14よりは、3.145のほうが、πの「直前」には相応しい。
　　　　　・しかし、3.145よりは、3.1459のほうが、πの「直前」には相応しい。
　　　　　：
　　　　　：

　・こんな具合で、
　　実数aの「直前」「直後」「両隣」は、確かにあるはずなのだけども、
　　これだと思って捕まえようとした途端、
　　もっと、実数aに近い「直前」「直後」「両隣」が必ず現れてくるので、
　　どこまでいっても、どの実数が実数aの「直前」「直後」「両隣」なのか、明示できなくなってしまうのだ。

　　どの実数が実数aの「直前」「直後」「両隣」なのか、明示できないということは、
　　　実数aの両隣（直前・直後）が、「Eに属す実数」なのかどうかも、明示できない。

　　だから、上記の定義に照らし合わせて、
 　「実数aが『Eの内点』である」がどうか判定しようとしても、
　　その結果を明示することは出来ないということになる。
　・こうした事態は、《切れ目がない》という実数の性質に起因する。
　　実数には《切れ目がない》から、
　　　実数aの「直前」「直後」「両隣」にあたる実数 は？
　　という発想が不適切になるのだ。
 　　ならば、
　　実数aの「直前」「直後」「両隣」ではなく、
　　実数aの前後をカバーする《切れ目がない》ゾーンに着目すれば、
　　もっと明確に「実数aが『Eの内点』 である」ということを定義できるのではないか。
 　　この発想で組み立てられたのが、下段の厳密な「内点」定義になる。






厳密的な「内点」定義　～　アイデアだけ　

「実数aが『《実数の集合E》の内点』である」とは、

　　実数aの前方から後方にかけて、
　　「Eに属す実数」に満たされた《切れ目のないゾーン》が、
　　カバーしている

ということ。

＊高木『解析概論』第1章12(p.29)では、
　　「aが点集合Sに属する一つの点Pに十分近い点がすべてSに属するとき、PをSの内点という」
　と定義。　


操作化された厳密な「内点」定義

　上記アイデアの《実数aの前方》《実数aの後方》《切れ目のないゾーン》を、
　操作化したのが、下記定義。

　・距離のみを用いて、《実数aの前方》《実数aの後方》《切れ目のないゾーン》を操作化
　　→　距離を用いた内点定義  　

　・開区間　を用いて、《実数aの前方》《実数aの後方》《切れ目のないゾーン》を操作化
　　→　開区間を用いた内点定義 　　

　・近傍概念を用いて、《実数aの前方》《実数aの後方》《切れ目のないゾーン》を操作化
　　→　近傍を用いた内点定義 　


【一般化】　R2における内点/Rnにおける内点/距離空間一般における内点

【性質】
　・「Aの内点」は、すべて、Aに属す。[小平『解析入門I』§1.6-b(p.56):R2]　　
　・int A⊂A⊂Aの閉包 　　[de la Fuente：2.4(a)(p.60);松坂『解析入門3』12.1-C(p.52;53)]
　・内点・外点・境界点の関係　/　触点と内点・外点・境界点との関係　/　内点・外点・境界点と集積点との関係　

【文献】
　・高木『解析概論』第1章12(p.29):特にRの例をあげず、一般的に。「aが点集合Sに属する一つの点Pに十分近い点がすべてSに属するとき、PをSの内点という」と定義。　
　・高橋『経済学とファイナンスのための数学』1.1集合Ⅱ開集合と閉集合-注1(p.5):R1において。
　・小平『解析入門I』§1.6-b(p.56):R2"inner point"
　・吹田・新保『理工系の微分積分学』pp.154-155;
　・松坂『集合・位相入門』第4章§1B(p.141);
　・松坂『解析入門3』12.1-C集合の内部・外部・境界・閉包(p.5２):
　・de la Fuente, Mathematical Methods and Models for Economists,2.4(a)Definition4.5(i)(p.59):距離空間一般において。
　・ルディン『現代解析学』2.20定義e(p.33):距離空間一般について。ε近傍で定義。「点pがEの内点とは、pの適当な近傍Nにたいし、N⊂Eが成立すること」　
　・Lang, Undergraduate Analysis,Chapter6§5Exercises2(p.131)
　・一楽『集合と位相―そのまま使える答えの書き方』定義3.3.3(pp.100-101)　：Rnにおいて。内部の点として定義。
　・能代『極限論と集合論』7章3(p.131)　:Rn
　・笠原『微分積分学』1.3(p.18):R2
　・杉浦『解析入門I』p.66:Rn
　・加藤『微分積分学原論』定義19.1(p.238)
　・瀬山『「無限と連続の数学」－微分積分学の基礎理論案内』定義2.6.3(p.153)：Rにおいて。

　・奥野鈴村『ミクロ経済学』数学附録Ⅰ-2-B(pp.262-3)Rn上


→内点トップ
→実数－《実数の集合》間の位置関係一覧
→トピック一覧：距離空間(R,d)
→総目次　

操作化された「内点」定義　：　距離を用いて操作化された表現

・「実数aが『《実数の集合E》の内点』である」とは、

　　《aからの距離ε》を、Eに応じた《ちょうどよい》値に設定することによって、　
　
　　　Eにすっぽり含まれる《aからの距離ε以内のゾーン》を最低一個はつくれる
　　　　つまり、《Eに属す実数》で埋め尽くした《aからの距離ε以内のゾーン》を最低一個はつくれる

　ということ。　　

・論理記号で表すと、

　「実数aが『Rの部分集合Eの内点』である」とは、

　(1)　∃ε>0　∀x∈R （　|x-a|<ε ⇒ x∈E　）
　ないし
　(2)　∃ε>0　∀x∈R （　x∈{ x'∈R | |x'-a|<ε } ⇒ x∈E　）
　ないし
　(3)　∃ε>0　{ x∈R | |x-a|<ε }⊂E　
　　　　　「あるε>0に対して、《aからの距離ε以内のゾーン》⊂E」「《aからの距離ε以内のゾーン》⊂Eを満たす距離εが存在する」
　
　　ということ。

【文献】

　目下、見当たらず。

　上記(3)は、「内点の定義－近傍表現」を、Uε(a)＝{ x∈R | |x-a|<ε }をつかって、書き換えただけ。　　
　上記(3)から(2)は、⊂の定義をつかって書き換えただけ。
　上記(2)から(1)は、命題関数P(x)の集合表現をつかって書き換えただけ。



→内点トップ
→実数－《実数の集合》間の位置関係一覧
→トピック一覧：距離空間(R,d)
→総目次　　

操作化された「内点」定義　：　開区間を用いて操作化された表現
・「実数aが『《実数の集合E》の内点』である」とは、
　
　　Eに応じた《ちょうどよい》値に、開区間 (a－ε, a＋ε) の幅εを決めてあげることによって、
　　　Eにすっぽり含まれる  (a－ε, a＋ε) を、最低一個はつくれる
　　　つまり、《Eに属す実数》で埋め尽くした (a－ε, a＋ε)を最低一個はつくれる

　ということ。　　

・論理記号で表すと、

　「実数aが『《実数の集合E》の内点』である」とは、

　　　∃ε>0　(a－ε, a＋ε)⊂E　　　

　　　　　　「ある開区間 (a－ε, a＋ε)に対して、(a－ε, a＋ε)⊂E」「(a－ε, a＋ε)⊂Eを満たす開区間 (a－ε, a＋ε)が存在する」　
　　　　　　「あるε>0に対して、(a－ε, a＋ε)⊂E」「(a－ε, a＋ε)⊂Eを満たす正数εが存在する」
　ないし

　　　∃ε>0　∀x∈(a－ε, a＋ε) 　x∈E　

　　ということ。

【文献】

　目下、見当たらず。
　上記は、「内点の定義－近傍表現」を、Uε(a)＝(a－ε, a＋ε)をつかって、書き換えただけ。　　


→内点トップ
→実数－《実数の集合》間の位置関係一覧
→トピック一覧：距離空間(R,d)
→総目次　
操作化された「内点」定義　：　近傍概念をもちいて操作化された表現

・「実数aが『Rの部分集合Eの内点』である」とは、
　「実数aの適当な近傍が、Eの点ばかりからなるということ。[能代『極限論と集合論』7章2定理3(p.131)。]

・操作的に言うと、

　「実数aが『Rの部分集合Eの内点』である」とは、
　
　　Eに応じた《ちょうどよい》値に、aのε近傍 Uε(a)の幅εを決めてあげることによって、
　　　Eにすっぽり含まれる Uε(a)を、最低一個はつくれる
　　　　つまり、《Eに属す実数》で埋め尽くしたUε(a)を最低一個はつくれる

　ということ。　　

・論理記号で表すと、

　「実数aが『Rの部分集合Eの内点』である」とは、

　　　∃ε>0　Uε(a)⊂E　　[松坂『解析入門3』12.1-C集合の内部・外部・境界・閉包(p.5２)]　

　　　　　　「あるUε(a)に対して、Uε(a)⊂E」「Uε(a)⊂Eを満たすUε(a)が最低一個は存在する」　
　　　　　　「あるε>0に対して、Uε(a)⊂E」[deLaFuente;高橋注1(p.5)]「Uε(a)⊂Eを満たす正数εが最低一個は存在する」

　　　∃ε>0　∀x∈Uε(a) 　x∈E　[上記を⊂の定義をつかって、高木『解析概論』第1章12(p.29)風に書き換えてみた。]

　ということ。　　　


　　　　R上の点集合の内点
　　　　R上の点集合の内点ではない点の例
　　　　R上の点集合の内点ではない点の例

【文献】

　・能代『極限論と集合論』7章2定理3(p.131)
　・松坂『解析入門3』12.1-C集合の内部・外部・境界・閉包(p.5２)
　・高橋『経済学とファイナンスのための数学』1.1集合Ⅱ開集合と閉集合-注1(p.5):R1において。
　・de la Fuente, Mathematical Methods and Models for Economists,2.4(a)Definition4.5(i)(p.59):距離空間一般において。
　・ルディン『現代解析学』2.20定義e(p.33):距離空間一般について。ε近傍で定義。「点pがEの内点とは、pの適当な近傍Nにたいし、N⊂Eが成立すること」　

→内点トップ
→実数－《実数の集合》間の位置関係一覧
→トピック一覧：距離空間(R,d)
→総目次　

【メモ】
※　{1/n|n∈N}のようなRの部分集合も図示する必要。[岡田『経済学･経営学のための数学』4.3(p.163)]
　　　　　　　　「点集合Eに属す点」と「点集合Eの内点」の異同。