�@���̖���P,Q�݂͌��Ɍ��������\�i�܂�A����P������Q�j�ł���B
�@�y ����P �z
| x��x0 |
�@�y ����Q �z
�@�@�@�@x0 �����������ǂ�������@{ xn }={ x1 , x2 , x3 , �c }�@�i�������Axn �� x0 �j�ɑ��Ă��A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���� { f ( xn ) }={ f ( x1 ) , f ( x2 ), f ( x3 ),�c} �@�� A�����������B
�@�@�@�@�@�܂�A�@�@[�@�� { xn }�@]�@[�@ xn �� x0 (n����) �� f ( xn)��A�@(n����)�@]
�@�@���Ȃ��H���ؖ��@
�@�@cf. �E�Ɍ�/���Ɍ��̏ꍇ�A�����������B
�@�@�����p��F���̘A�����𐔗�̎�������������/�R�[�V�[�̔������(�\�����̏ؖ�)
| �@ |
||||
| �i��P�jx2��4 (x��2) (�a�B�O���w�����ϕ��xp.26) �@�@�@��f(x)= x2�ɂ����āA2�Ɏ�������悤 ��X���̐���Ƃ��āA 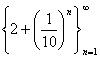 ���Ƃ�[n������2�Ɏ���]�B ���Ƃ�[n������2�Ɏ���]�B�@�@�@���̑��ɂ���Ă����鐔��́A{4+4 (1/10)n+ (1/10)2n }�B����́An������4�Ɏ����B �@�@�@2�Ɏ�������悤��X���̐���Ƃ��āA 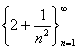 ���Ƃ�[n������2�Ɏ���]�B ���Ƃ�[n������2�Ɏ���]�B�@�@�@���̑��ɂ���Ă����� ����́A{4+4/n2+1/n4 }�B������An������4�� �����B |
||||
| �@ |
||||
| �i��2�j�@�@x��0
�̂Ƃ��@f (x)= sin (1/x)�͋Ɍ��l���������������Ȃ��@�i�_�J�E�Y��w�o�ϊw�̂��߂�
���w�����xp.94.�j �@�@�@X={ x��R | 0��x }, Y=R�� ���Af (x) = sin (1/x)�Ƃ���B �@�@�@0�Ɏ�������悤��X���̐���Ƃ��āA 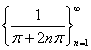 ���Ƃ�[n������0�Ɏ���]�B ���Ƃ�[n������0�Ɏ���]�B�@�@�@�@�@���̑��ɂ���Ă����� ����́A{ 0,0,0,�c }�B���̐���́An������0�Ɏ����B �@�@�@0�Ɏ�������悤��X���̐���Ƃ��āA 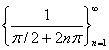 ���Ƃ�[n������0�Ɏ���]�B ���Ƃ�[n������0�Ɏ���]�B�@�@�@�@�@�@���̑��ɂ���Ă���� �鐔��́A{ 1,1,1,�c }�B���̐���́An������1�Ɏ����B �@�@�@����āAx��0�ւ̋߂Â����A0�֎�������x���̐���̑I�ѕ��ŁA���̑��ɂ���č���鐔��̋Ɍ����ς���Ă���B �@�@�@���������āAx��0�̂Ƃ� f (x)= sin(1/x)�͋Ɍ��l�������������� �Ȃ����ƂɂȂ�B�@�@�@�@ |
||||
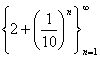 ���Ƃ�B[��������2�Ɏ���]
���Ƃ�B[��������2�Ɏ���]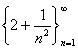 ���Ƃ�B[n������2�Ɏ���]
���Ƃ�B[n������2�Ɏ���]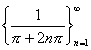 ���Ƃ�B[��������0�Ɏ���]
���Ƃ�B[��������0�Ɏ���]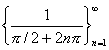 ���Ƃ�B[��������0�Ɏ���]
���Ƃ�B[��������0�Ɏ���]