�s��ϕ�indefinite integral �������͐ϕ����̒�`�Ɛ����F
|
|
|
��[�g�s�b�N�ꗗ�F�s��ϕ��E�ϕ���] �����ڎ� |

|
��[�g�s�b�N�ꗗ�F�s��ϕ��E�ϕ���] �����ڎ� |
|
��[�g�s�b�N�ꗗ�F�s��ϕ��E�ϕ���] �����ڎ� |
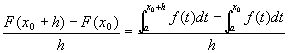 �@��B
�@��B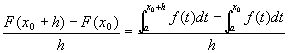 �@��B
�@��B|
��[�g�s�b�N�ꗗ�F�s��ϕ��E�ϕ���] �����ڎ� |
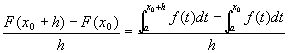 �@��B
�@��B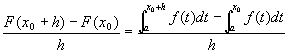 �@��B
�@��B|
��[�g�s�b�N�ꗗ�F�s��ϕ��E�ϕ���] �����ڎ� |
�@�@
�@