��ϕ��̌v�Z�Q�F�u���ϕ��E�����ϕ��@ �F�@�g�s�b�N�ꗗ�@�E�u���ϕ�(�ؖ�)�@ �E�����ϕ��@ ��1�ϐ����̒�ϕ��֘A�y�[�W�F �@����ϕ��̒�`/����/���n�� �@�������t����ϕ�/�ϕ��� (�s��ϕ�) �@����͊w�̊�{�藝 ��1�ϐ����̐ϕ��֘A�y�[�W�F �@��L�E���̍L�`�ϕ�/������Ԃ̍L�`�ϕ�/�X�`���`�F�X�ϕ� �����ϐ����̐ϕ��֘A�y�[�W�F �@��`���2�ϐ����̐ϕ�/��ʏW�����2�ϐ����̐ϕ��@ �����ڎ� |
|
 �@
�@|
��[�g�s�b�N�ꗗ�F�u���ϕ��E�����ϕ�] �����ڎ� |
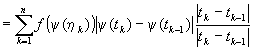 �@�@��1=|tk�|tk-1|/|tk+1�|tk-1|
�@�@��1=|tk�|tk-1|/|tk+1�|tk-1| 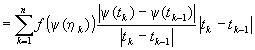
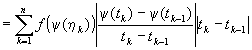 �@����Βl�̐����F|x/y|=|x|/|y|�@(y��0)
�@����Βl�̐����F|x/y|=|x|/|y|�@(y��0)


|
��[�g�s�b�N�ꗗ�F�u���ϕ��E�����ϕ�] �����ڎ� |
|
��[�g�s�b�N�ꗗ�F�u���ϕ��E�����ϕ�] �����ڎ� |
�@