コンパクト空間・コンパクト集合・Compactの定義[数学についてのwebノート]

コンパクト性の定義

[トピック一覧：コンパクト性]
　定義：コンパクト空間、コンパクト集合、相対コンパクト、点列コンパクト、有限交差性、　
※位相関連ページ：開集合系・開集合、閉集合系・閉集合、近傍系・近傍、
　　　　　　　　　開核作用素・開核、閉包作用素・閉包
　　　　　　　　　位相空間・位相の定義、誘導位相、部分位相空間・相対位相
※コンパクト性関連ページ：R¹上のコンパクト集合、R²上のコンパクト集合、Rⁿ上のコンパクト集合　

→総目次

定義：コンパクト位相空間
[松坂『集合・位相入門』5章§2-Aコンパクト位相空間(p.209):丁寧;斉藤『数学の基礎：集合・数・位相』5.2.2 (p.142);矢野『距離空間と位相構造』4.1.1節コンパクト空間(p.123);『岩波数学事典』項目14位相空間Sコンパクト性;]
(設定)
　　X　　　:　　(普遍)集合　　
　　O　　　:　　Xの開集合系　
　　(X, O)　:　　Xを台にして位相としてOを入れた位相空間　　
(定義)
　　Xがコンパクトないしコンパクト空間であるとは、
　　Xの任意の開被覆が有限部分被覆をもつこと。
(定義の詳細な説明)
　　手順1:　Xの任意の開被覆をЦ={ U_λ}_λ_∈_Λとおく。　
　　　　　　すなわち、
　　　　　　以下の2条件を満たすXの部分集合族{ U_λ}_λ_∈_ΛをЦとおく。
　　　　　　　・条件1: Xを被覆すること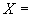　　　　　
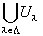
　　　　　　　・条件2:開集合のみからなること　　任意のλ∈Λに対して、U_λ∈O　　
　　手順2:　Ц={ U_λ}_λ_∈_Λの有限部分被覆{U₁,U₂,U₃, …,U_n}が存在するかどうかチェック。　
　　　　　　すなわち、
　　　　　　{U_λ}_λ_∈_Λから、X=U₁∪U₂∪U₃∪…∪U_nを満たす、「集合の有限列」{U₁,U₂,U₃, …,U_n}を
　　　　　　取り出せるかどうかをチェック。　
　　手順3:　Ц={U_λ}_λ_∈_Λの有限部分被覆が存在しないならば、
　　　　　　　すなわち、{U_λ}_λ_∈_Λから、どういう組合せで{U₁,U₂,U₃, …,U_n}をひねり出してきても、
　　　　　　　　　　　　　X=U₁∪U₂∪U₃∪…∪U_n　　
　　　　　　　　　　　　と出来ないならば、
　　　　　　Xは、コンパクト空間ではない。
　　　　　　Ц={U_λ}_λ_∈_Λの有限部分被覆が存在するならば、
　　　　　　　すなわち、{U_λ}_λ_∈_Λから、{U₁,U₂,U₃, …,U_n}をうまく選べば、
　　　　　　　　　　　　　X=U₁∪U₂∪U₃∪…∪U_n　を満たす{U₁,U₂,U₃, …,U_n}をつくれるならば、　
　　　　　　手順4へ進む。
　　手順４：Xの開被覆を、他のものに変えて、手順1-3をテストしてみる。
　　　　　　Xのあらゆる開被覆に対して、有限部分被覆が存在するならば、　　
　　　　　　Xは、コンパクト空間である。
　
Cf.コンパクト距離空間

→[トピック一覧：コンパクト性]

→総目次　

定義：位相空間におけるコンパクト集合
　　[松坂『集合・位相入門』5章§2-Aコンパクト位相空間(pp.210-11):丁寧;
　　斉藤『数学の基礎：集合・数・位相』5.2.3 (p.142);矢野『距離空間と位相構造』4.1.1節コンパクト空間(p.123);
　　『岩波数学事典』項目14位相空間Sコンパクト性;]
cf. R¹上のコンパクト集合、R²上のコンパクト集合　
(設定)
　X:　　　　(普遍)集合　　
　(X, O) :　　位相空間　　
　A:　　Xの部分集合　
(定義1)
位相空間(X, O)の部分集合Aがコンパクトないしコンパクト集合であるとは、
AにおけるOの相対位相O_A={O∩A|O∈O }　に関して、Aがコンパクト空間であること。
つまり、位相空間(X, O)の部分位相空間(A,O_A)がコンパクト空間であること。
(定義1の詳細な説明)　
Aを普遍集合とみたてたときのAの任意の開被覆、
すなわち、以下の2条件を満たすAの部分集合族を{ U_λ}_λ_∈_Λとおく。
　　　・条件1: 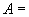　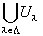　…(1-1)
　　　・条件2: 任意のλ∈Λに対して、U_λ∈O_A= {O∩A|O∈O }　…(1-2)
Aのどの開被覆Ц={ U_λ}_λ_∈_Λからも、有限部分被覆を、
　　すなわち、A=U₁∪U₂∪U₃∪…∪U_nを満たす「集合の有限列」{U₁,U₂,U₃, …,U_n}を、
取り出せるならば、
位相空間(X, O)の部分位相空間(A,O_A)はコンパクト空間であるが、
このとき、Aがコンパクトないしコンパクト集合であるという。
(定義2)
位相空間(X, O)の部分集合Aがコンパクトないしコンパクト集合であるとは、
部分集合Aの任意の「Xにおける開被覆」が、「Xにおける有限部分被覆」をもつこと。
(定義2の詳細な説明)
　　手順1:　Aの任意の「Xにおける開被覆」をЦ={ U_λ}_λ_∈_Λとおく。　
　　　　　　すなわち、
　　　　　　以下の2条件を満たすXの部分集合族{ U_λ}_λ_∈_ΛをЦとおく。
　　　　　　　・条件1: Aを被覆すること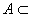　　　　　
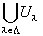
　　　　　　　・条件2: 開集合のみからなること　　任意のλ∈Λに対して、U_λ∈O　　
　　手順2:　Ц={ U_λ}_λ_∈_Λの有限部分被覆{U₁,U₂,U₃, …,U_n}が存在するかどうかチェック。　
　　　　　　すなわち、
　　　　　　{U_λ}_λ_∈_Λから、A⊂U₁∪U₂∪U₃∪…∪U_nを満たす、「集合の有限列」{U₁,U₂,U₃, …,U_n}を
　　　　　　取り出せるかどうかをチェック。　
　　手順3:　Ц={U_λ}_λ_∈_Λの有限部分被覆が存在しないならば、
　　　　　　　すなわち、{U_λ}_λ_∈_Λから、どういう組合せで{U₁,U₂,U₃, …,U_n}をひねり出してきても、
　　　　　　　　　　　　　A⊂U₁∪U₂∪U₃∪…∪U_n　　
　　　　　　　　　　　　と出来ないならば、
　　　　　　Aは、コンパクト集合ではない。
　　　　　　Ц={U_λ}_λ_∈_Λの有限部分被覆が存在するならば、
　　　　　　　すなわち、{U_λ}_λ_∈_Λから、{U₁,U₂,U₃, …,U_n}をうまく選べば、
　　　　　　　　　　　　　A⊂U₁∪U₂∪U₃∪…∪U_nを満たす{U₁,U₂,U₃, …,U_n}をつくれるならば、　
　　　　　　手順4へ進む。
　　手順４：Aの「Xにおける開被覆」を、他のものに変えて、手順1-3をテストしてみる。
　　　　　　Aのあらゆる「Xにおける開被覆」に対して、有限部分被覆が存在するならば、　　
　　　　　　Aは、コンパクト集合である。
　→コンパクト集合
　→[トピック一覧：コンパクト性]　
(定義1と定義2が同値であることの証明) [斉藤『数学の基礎：集合・数・位相』5.2.4(p.142);]
コンパクト集合の定義1と定義2は、同値である。
これを示すために、
まず、定義1が成立すれば定義２が成立することを証明し、
次に、定義2が成立すれば定義1が成立することを証明する。
　→コンパクト集合
　→[トピック一覧：コンパクト性]　
[証明：定義1 ⇒定義2]
(設定)　　
　　X:　　　　(普遍)集合　　
　　O　　　:　　Xの開集合系　
　　(X, O) :　　位相空間　　
　　A:　　Xの部分集合　
　　O_A:　AにおけるOの相対位相 {O∩A|O∈O }。開集合系となる(なぜ？→証明）　
　　(A,O_A)：　位相空間(X, O)の部分位相空間　
(仮定：定義1)
位相空間(X, O)の部分位相空間(A,O_A)がコンパクト空間であること。
（本題）
step1: 仮定を、コンパクト空間の定義にもどって詳しく言い換え。
Aを普遍集合とみたてたときのAの任意の開被覆、
すなわち、以下の2条件を満たすAの部分集合族を{ U_λ}_λ_∈_Λとおく。
　　　・条件1: 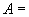　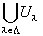　…(1-1)
　　　・条件2: 任意のλ∈Λに対して、U_λ∈O_A= {O∩A|O∈O }　…(1-2)
仮定より、Aのどの開被覆Ц={ U_λ}_λ_∈_Λからも、有限部分被覆を、
　　すなわち、A=U₁∪U₂∪U₃∪…∪U_nを満たす「集合の有限列」{U₁,U₂,U₃, …,U_n}を、
取り出せる。…(1-3)
step2:
部分集合Aの任意の「Xにおける開被覆」、
すなわち、以下の2条件を満たすXの部分集合族を、{ V_λ}_λ_∈_Λとおく。
　　　　　　　・条件1: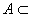 　　
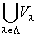
　　　　　　　・条件2: 任意のλ∈Λに対して、V_λ∈O　　
step3:
　Xの部分集合族{ V_λ∩A }_λ_∈_Λは、(1-1)(1-2)を満たすので、
　「Aを普遍集合とみたてたときのAの開被覆」の一つとなる。
　すると、(1-3)より、
　{ V_λ∩A }_λ_∈_Λから、有限部分被覆を、
　すなわち、A=(V₁∩A)∪(V₂∩A)∪(V₃∩A)∪…∪(V_n∩A)を満たす「集合の有限列」を、…(3)
　取り出せることになる。
　(3)に出てくる、V₁,V₂,V₃, …,V_nを並べて、「集合の有限列」{V₁,V₂,V₃, …,V_n}をつくる。
　これらは、部分集合Aの任意の「Xにおける開被覆」{ V_λ}_λ_∈_Λ(→step2)の有限部分被覆となっている。
　なぜなら、
　　　　　・{V₁,V₂,V₃, …,V_n}は、{ V_λ}_λ_∈_Λのなかから、
　　　　　　　「Xの部分集合」を有限n個とってきて並べた「Xの部分集合列」　　　
　　　　　・(3)より、A=(V₁∩A)∪(V₂∩A)∪(V₃∩A)∪…∪(V_n∩A)　
　　　　　　　　　　　=(V₁∪V₂∪V₃∪…∪V_n) ∩A　　（∵分配則）　　
　　　　　　この、A= (V₁∪V₂∪V₃∪…∪V_n) ∩Aは、
　　　　　　A⊂V₁∪V₂∪V₃∪…∪V_n　と同値。(∵)　
　　　　　以上2点より、(3)に出てくる{V₁,V₂,V₃, …,V_n}は、{ V_λ}_λ_∈_Λ(→step2)の有限部分被覆。
step4:
以上から、仮定=定義1のもとで、「部分集合Aの任意の「Xにおける開被覆」が、「Xにおける有限部分被覆」をもつこと」、すなわち、コンパクト集合の定義2が成立することが示された。
　→コンパクト集合の定義1と定義2が同値であることの証明トップ　
　→コンパクト集合
　→[トピック一覧：コンパクト性]　

[証明：定義2 ⇒定義1 ]
(設定)　　
　　X:　　　　(普遍)集合　　
　　O　　　:　　Xの開集合系　
　　(X, O) :　　位相空間　　
　　A:　　Xの部分集合　
(仮定：定義2)
部分集合Aの任意の「Xにおける開被覆」が、「Xにおける有限部分被覆」をもつ
（本題）
step1:　
Aを普遍集合とみたてたときのAの任意の開被覆、
すなわち、以下の2条件を満たすAの任意の部分集合族を{ U_λ}_λ_∈_Λとおく。
　　　・条件1: 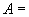　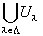　…(1-1)
　　　・条件2: 任意のλ∈Λに対して、U_λ∈O_A= {O∩A|O∈O }　…(1-2)　　
step2:　
(1-2)より、各λに対して、Aとの重複部分がU_λとなる「Xの開集合」O_λが存在する。
　すなわち、　・条件1: 任意のλ∈Λに対して、O_λ∈O　　　…(2-1)
　　　　　　　・条件2: 任意のλ∈Λに対して、O_λ∩A= U_λ　…(2-2)　
　　　　　　をともに満たす「Xの部分集合族」{ O_λ}_λ_∈_Λが存在する。　　
Step3:　
「Xの部分集合族」{O_λ}_λ_∈_Λは、部分集合Aの「Xにおける開被覆」である。
　　なぜなら…。
　　(2-2)より、O_λ⊃(O_λ∩A)=U_λ　（∵）　　　
　　ゆえに、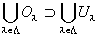　　　　　
　　これと(1-1)をあわせて考えると、
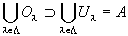　　　　　…(3)
　　よって、{ O_λ}_λ_∈_Λは、(2-1)と(3)を満たすので、部分集合Aの「Xにおける開被覆」である。
Step4:　
仮定により、部分集合Aの「Xにおける開被覆」{ O_λ}_λ_∈_Λは、「Xにおける有限部分被覆」をもつ。
すなわち、{ O_λ}_λ_∈_Λから、
　　　　　　　　　A⊂O₁∪O₂∪O₃∪…∪O_n　　…(4)　　　　　　を満たす「集合の有限列」{O₁,O₂,O₃, …,O_n}を取り出せる。　　
Step5:　
{O₁∩A,O₂∩A,O₃∩A, …,O_n∩A }は、
step1で「Aを普遍集合とみたてたときのAの任意の開被覆」とした{ O_λ}_λ_∈_Λの有限部分被覆となる。
なぜならば、　　
　・(1-2)および(2-2)より、{O₁∩A,O₂∩A,O₃∩A, …,O_n∩A }は、
　　　{ U_λ}_λ_∈_Λから取り出した「集合の有限列」{U₁,U₂,U₃, …,U_n}である。　
　・(4)より、A= (O₁∪O₂∪O₃∪…∪O_n) ∩A　　(∵)　　
　　　　　　　=(O₁∩A)∪(O₂∩A)∪(O₃∩A)∪…∪(O_n∩A)　（∵分配則）　　
　　　　　つまり、A=(O₁∩A)∪(O₂∩A)∪(O₃∩A)∪…∪(O_n∩A)　
　以上2点から、{O₁∩A,O₂∩A,O₃∩A, …,O_n∩A }は、{ U_λ}_λ_∈_Λの有限部分被覆だといえる。
Step6:　
以上から、定義2が成立するならば、「『Aを普遍集合とみたてたときのAの任意の開被覆』が有限部分被覆をもつこと」すなわち定義1「位相空間(X, O)の部分位相空間(A,O_A)がコンパクト空間であること」が成立することが示された。　　

→コンパクト集合の定義1と定義2が同値であることの証明トップ　
→コンパクト集合
→[トピック一覧：コンパクト性]　
→総目次　

定義：相対コンパクト relatively compact　
[矢野『距離空間と位相構造』4.1.1節コンパクト空間(p.123);『岩波数学事典』項目14位相空間Sコンパクト性;]
(設定)
　　X:　　　　(普遍)集合　　
　　(X, O) :　　位相空間　　
　　A:　　Xの部分集合　
(定義1)
Xの部分集合Aが相対コンパクトであるとは、
Aの閉包がコンパクトであること。

→[トピック一覧：コンパクト性]

→総目次　

定義：点列コンパクトsequentially compact
　斉藤『数学の基礎：集合・数・位相』5.2.29点列コンパクト(p.153)を見よ。

cf.　距離空間(R¹,d)における点列コンパクト、距離空間(R²,d)における点列コンパクト、
　　距離空間(Rⁿ,d)における点列コンパクト、距離空間一般における点列コンパクト、

定義：有限交叉性finite intersection property　　
松坂『集合・位相入門』5章§2-Aコンパクト位相空間(p.210);斉藤『数学の基礎：集合・数・位相』5.2.5 (p.143);矢野『距離空間と位相構造』4.1.1節コンパクト空間(p.125);『岩波数学事典』項目14位相空間Sコンパクト性;
を見よ。

→[トピック一覧：コンパクト性]

→総目次　

定理：コンパクト性と同値な条件

→[トピック一覧：コンパクト性]

→総目次　

定理：Tychonoffチコノフの定理・チホノフの定理
[矢野『距離空間と位相構造』4.1.3節コンパクト性の遺伝定理4.10(p.136):有限直積の場合の証明;
斉藤『数学の基礎：集合・数・位相』5.2.12 (p.144): 有限直積;5.2.22(pp.149-51):無限直積:;
松坂『集合・位相入門』5章§2-B定理13(p.212);]
コンパクト空間の直積空間はコンパクトである。また、逆も成り立つ。

→[トピック一覧：コンパクト性]

→総目次　

Reference

日本数学会編集『岩波数学事典(第三版)』岩波書店、1985年、項目14位相空間Sコンパクト性。
矢野公一『距離空間と位相構造』共立出版、1997年。 4章コンパクト空間4.1コンパクト性4.1.1コンパクト空間(p.123-125)
斉藤正彦『数学の基礎：集合・数・位相』東大出版会、2002年。第5章位相空間(その2)§2コンパクト性5.2.1-6 (p.142-3);5.2.29点列コンパクト(p.153)
松坂和夫『集合・位相入門』岩波書店、1968年。第5章§2コンパクト性-Aコンパクト位相空間(pp.208-211)。
彌永昌吉・彌永健一『岩波講座基礎数学：集合と位相　I・II』岩波書店、1977年。 II.位相第3章コンパクト集合§3.1コンパクト位相空間-§3.2有限交叉性とコンパクト性(pp.243-8)
志賀浩二『位相への30講』朝倉書店、1988年、第27講コンパクト空間と連結空間(pp.187-172)。
西村和雄『経済数学早わかり』日本評論社、1982年、第六章位相数学§3コンパクト集合3.1-3.2 (pp.295-300)。卑近な例もまじえつつ、具体的に説明。
佐久間一浩『集合・位相―基礎から応用まで―』共立出版、2004年、4.3節pp.87-92。

→[トピック一覧：コンパクト性]

→総目次　