集合関数　

　　　　　
→集合論目次・総目次

定義：集合関数set function・区間関数interval function・点関数point function

　　　　[『岩波数学辞典（第三版）』項目163 (p.432);伊藤『ルベーグ積分』I§3(p.11)
　　　　　高木貞治『解析概論』108節集合の測度(pp.403-5) ; 高橋『経済学とファイナンスのための数学』p.28;
　　　　　クラメール『統計学の数学的方法:第1巻』6.2集合関数と点関数(pp.47-48)]


（舞台設定）

　X　：　集合、
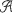　　：　集合Xの部分集合系(族)　

（本題）

集合Xで定義された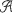 -集合関数とは、
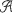　　に属す「集合Xの部分集合」A
　　　　　　　すなわち、A⊂X かつ A∈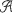を満たす集合A
　　に対して定義された関数のこと。
　　　（つまり、定義域が集合Xの部分集合系(族)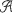となる関数。）

　また、
　集合関数で、値が実数値であるものを、実数値集合関数 real valued set function、
　集合関数で、値も集合(値域が集合系(集合族))であるものを、集合値関数と呼ぶ。　　　
　実数全体の集合Rないしその直積Rkで定義された集合関数で、定義域がRないしRkでの左半開区間であるものを、

　　　　　　特に、区間関数interval functionと呼ぶことがある。
これに対して、
集合Xで定義された点関数とは、　　
　　集合Xに属す各元に対して定義された関数であり、これは、通常いうところの「写像」「関数」のこと。
　　→実数値関数　
※特殊な集合関数：有限加法的測度、測度、完全加法的集合関数、
※集合関数の例：リーマン積分、区間の長さ、矩形の面積、直方体の体積、Rn区間のn次元体積、
　　　　　　　　　R上区間塊の長さ、R2上区間塊の面積、R3上区間塊の体積、Rn上区間塊のn次元体積

reference

日本数学会編集『岩波数学事典(第三版)』 岩波書店、1985年。項目162A(pp.428-429), 163 (p.432)
伊藤清三『ルベーグ積分』I予備概念§3点関数と集合関数(p.11-3)
高橋一『経済学とファイナンスのための数学』新世社、1999年。 pp.1-4.
Cramer, Harald,1946 Mathematical Methods of Statistics, Princeton UP.
=クラメール『統計学の数学的方法:第1巻』東京図書、1973年、6.2集合関数と点関数(pp.47-48)。
高木貞治『解析概論:改訂第3版』岩波書店、1983年、第9章Lebesgue積分,I.概括論, 108集合の測度(pp.403-5).