定理：距離空間(Rn,d)上のε近傍と位相
[松坂『集合・位相入門』第6章B(p.237); 彌永『集合と位相』§2.3例2.12(p.188);]
点Pのすべてのε近傍をあつめた集合系は、点Pの基本近傍系をなす。
定理：距離空間(Rn,d)上の開集合と位相
[松坂『集合・位相入門』4章§1D(p.144)問題3(p.151);6章B(p.237); 志賀『位相への30講』第3項(pp.22-23)
斉藤『数学の基礎：集合・数・位相』第四章§5項目4.5.3(p.125);
矢野『距離空間と位相構造』1.3.2開集合命題4.15(p.41)]
（本題）
距離空間(Rn,d)における(距離空間の文脈でいう)開集合をすべてあつめた集合系Odは、
(位相の文脈でいう)開集合系をなす。
ゆえに、Odは、集合Rnにおける位相となる。
この意味で、Odは、距離dの定める位相とも呼ばれる。
（意義）
この定理は、
「集合Rnに距離dを定義しさえすれば、集合Rnに位相を定めたことになる」、
「距離空間(Rn,d)には、いつでも、位相空間(Rn, Od)がついてくることになる」
という重大な事態を意味している。
つまり、
step1.集合Rnに距離dを定義して、距離空間(Rn,d)をつくると、距離dから、ε近傍が定義される、
(ε近傍の定義による。ε近傍の定義は距離dにのみ依存する。)
step2. ε近傍が定義されれば、距離空間(Rn,d)における(距離空間の文脈でいう)開集合も定義される、
(距離空間の文脈でいう開集合の定義による)
step3. 距離空間(Rn,d)における(距離空間の文脈でいう) 開集合をすべてあつめた集合系は、
位相の文脈でいう開集合系をなす。
（この定理による）
step4. 集合Rnに位相の文脈でいう開集合系が定まるならば、集合Rnに位相が定められ、
集合Rnとその開集合系の組は、位相空間となる。
（位相、位相空間の定義による）
（証明）
距離空間(Rn,d)における(距離空間の文脈でいう)開集合をすべてあつめた集合系Odは、
(位相の文脈でいう)開集合の公理を満たすことを示す。
[志賀『位相への30講』第3項(pp.20-23);斉藤『数学の基礎：集合・数・位相』第四章§5項目4.5.3(p.125);
矢野『距離空間と位相構造』1.3.2開集合命題4.15(p.41)]
Step1: 距離空間(Rn,d)上の開集合をすべてあつめた集合系は、開集合系の第1条件を満たす。
距離空間(Rn,d)上の開集合の定義より、
Rn全体、空集合φも、距離空間(Rn,d)上の開集合の一例（→理由）。
ゆえに、距離空間(Rn,d)上の開集合をすべてあつめた集合系Odは、
開集合系の第1条件： Rn ∈Od かつ φ∈Od
を満たす。
Step2: 距離空間(Rn,d)上の開集合をすべてあつめた集合系は、開集合系の第2条件を満たす。
距離空間(Rn,d)上の開集合の性質より、
距離空間(Rn,d)上の開集合をすべてあつめた集合系Odは、
開集合系の第2条件(∀O1,O2∈O) (O1∩O2∈O)を満たす。
Step3: 距離空間(Rn,d)上の開集合をすべてあつめた集合系Odは、開集合系の第3条件を満たす。
距離空間(Rn,d)上の開集合をすべてあつめた集合系Odは、
距離空間(Rn,d)上の開集合の性質より、
開集合系の第3条件
∀Oλ∈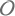
(λ∈Λ) にたいして、 
∈
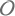を満たす。
Reference
日本数学会編集『岩波数学事典(第三版)』岩波書店、1985年、項目14位相空間、項目92距離空間(pp.253-256)、項目409ユークリッド幾何学(pp.1225-1229)、項目410ユークリッド空間 (pp.1229-1230).
矢野公一『距離空間と位相構造』共立出版、1997年。 1章距離空間1.3.2開集合(pp.40-41)
斉藤正彦『数学の基礎：集合・数・位相』東大出版会、2002年。第4章§5項目4.5.3(p.125)
松坂和夫『集合・位相入門』岩波書店、1968年。4章§1D(p.144)問題3(p.151);6章B(p.237);
志賀浩二『位相への30講』朝倉書店、1988年、第3項(pp.22-23)。
彌永昌吉・彌永健一『岩波講座基礎数学：集合と位相 I・II』 岩波書店、1977年。 II.位相第2章位相空間§2.1閉包写像と位相空間-§2.3近傍(pp.173-190)