《関数の右極限》の《数列の収束》への言い換え
※杉浦『解析入門』p.53における普通の極限・片側極限を包括した定理を自力でカスタマイズしたものなので要確認。
以下の命題Pと命題Qは互いに言い換え可能 （ つまり、命題P⇔命題Q ）。
命題P: x0における f (x)の右極限はA。
命題Q: ・xn →x0 (n→∞) (つまりx0に収束する)
※x0は後出の数列 { xn }の第0項という意味ではないので注意
かつ、
・任意のn∈N についてx0＜xn
を満たす限りで任意につくった(どんな)数列{ xn }={ x1 , x2, x3,…}に対しても、
f (xn) →A (n→∞) (つまり数列 { f ( xn) }={ f ( x1 ) , f ( x2 ) , f ( x3 ) ,…}がAに収束する)
cf.普通の極限/左極限の場合、これらを包括して。
※利用例：関数の右連続性を数列の収束へ言いかえる、コーシーの判定条件(十分性の証明)
[証明：Ｐ⇒Ｑ]
・P ： x0におけるf(x)の右極限はA。すなわち、f(x)→A (x→x0＋0) …(1)
・xn →x0 (n→∞) …(2)
・任意のn∈N についてx0＜xn …(3)
本論：(1)(2)(3)の仮定下で Q: f (xn) →A (n→∞) が成り立つことを示す。
(step1)仮定(1)の確認。
右極限の厳密な定義に従うと、(1)はすなわち、
任意の正数εに対して、ある正の実数δが存在して、
「0＜ x−x0 ＜δならば、| f(x)−A|＜ε」
すなわち「x∈ ( x0 , x0＋δ)ならば、f(x) ∈ ( A−ε,A＋ε) 」
を成り立たせる、ということ。…(4)
(step2)仮定(2)(3)の確認。
数列の収束の定義に従うと、(2)はすなわち、
任意の（どんな小さな）正の実数ε’に対して（でも）、ある（十分大きな）自然数Nが存在して、
「 n≧Nならば、| xn−x0|＜ε’」
すなわち、「 n≧Nならば、xn ∈ ( x0−ε’, x0＋ε’) 」
を成り立たたせる
ということだが、ただし(3)より、「 任意のn∈N についてx0＜xn 」 なので、
任意の（どんな小さな）正の実数ε’に対して（でも）、ある（十分大きな）自然数Nが存在して、
「 n≧Nならば、xn−x0＜ε’」
すなわち、「 n≧Nならば、xn ∈ ( x0 , x0 ＋ε’) 」
を成り立たたせる…(5)
となる。
(step3)
ε’はどんな正の実数でもいいというので、
ε’として(4)で定まるδをとっても、(5)はそのまま成り立つ。
すなわち、
(4)で定まった如何なるδに対してであろうとも、ある（十分大きな）自然数Nが存在して、
「 n≧Nならば、 xn−x0＜δ 」 を成り立たたせる …(6)
ということ。
(step4)
(6)で定まった自然数N以上の項についてみると、
xn−x0＜δ
が成り立つ。
ならば、(4)より、(6)で定まった自然数N以上の項については、
はじめに決めた任意の正数εに対して
| f(xn)−A |＜ε
が成り立つといえる。
(step5)仕上げ
数列の収束の定義から、これを以下の様に表現してよい。
f (xn)→A （ n→∞ ）
[証明：Q⇒P]
仮定Q：f (xn) →A (n→∞) …(1)
ただし、数列 { xn }は、
xn →x0 (n→∞) …(2)
任意のn∈N についてx0＜xn …(3)
を満たす限りで任意の数列(をどのようにとってもよい)。
結論P： f(x) →A (x→x0＋0) …(4)
（方針）：Q⇒Pを示すのに、その対偶、すなわち「Pが不成立」⇒「Qが不成立」を示す。
結論P「(4): f(x) →A (x→x0＋0)」が成り立たないなら、
仮定Q「(1): f (xn) →A (n→∞)（{ xn }は、(2)(3)を満たす限りで任意の数列）」も成り立たない、
ことを示す。
本論：
(step1) 「Pが成り立たない」「(4)が成り立たない」という仮定の確認。[中内『ろんりの練習帳』118-122。]
「 (4): f(x) →A (x→x0＋0)が成り立たない」と仮定する。
この仮定は、右極限の定義を用いて正確にとらえると、
任意の（どんな）正の実数ε0に対して（でも）、
「 0＜x−x0 ＜δならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ ( x0, x0＋δ)ならば、 f(x) ∈ ( A−ε0 ,A＋ε0 ) 」
を任意のxについて成り立たせる、ある正の実数δが存在するということ
の否定、すなわち、¬ ( ∀ε0 ＞0 ∃δ＞0 ∀x ( 0< x−x0＜δ⇒ | f (x)−A|＜ε0) ) となる。
＊ ＊ ＊
これは、
「 0＜x−x0 ＜δならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ ( x0, x0 ＋δ) ならば、 f(x) ∈ ( A−ε0 , A＋ε0 ) 」
を任意のxについて成り立たせる、ある正の実数δが、
任意の（どんな）正の実数ε0に対して（でも）、存在するとは限らない
ということを意味するので、
「 0＜x−x0 ＜δならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ ( x0, x0 ＋δ) ならば、 f(x) ∈ ( A−ε0 , A＋ε0 ) 」
を任意のxについて成り立たせる正の実数δを存在させないような正の実数ε0が(少なくとは一つは)存在する
と書き換えられる。
厳密に言えば、前の論理式を、¬ ( ∀ A(x) x P(x) )と(∃A(x) x) (¬P(x) )が言い換え可能であることを用いて、
∃ε0＞0 ¬ ( ∃δ＞0 ∀x ( 0< x−x0＜δ⇒ | f (x)−A|＜ε0 ) )
と書き換えられる、となる。
＊ ＊ ＊
「…を成り立たせる正の実数δを存在させない」というのは、「どんな風に正の実数δをとっても…を成り立たせない」といっても同じことなので、先の命題は、
「 0＜x−x0 ＜δならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ ( x0, x0 ＋δ) ならば、 f(x) ∈ ( A−ε0 , A＋ε0 ) 」
を任意の(すべての)xについて成り立たせることを、
どんな風に正の実数δをとっても成り立たせない正の実数ε0が(少なくとは一つは)存在する」
と書き換えられる。
厳密に言えば、前の論理式を、¬ ( ∃A(x) x P(x) )と(∀A(x) x) (¬P(x) )が言い換え可能であることを用いて、
( ∃ε0 ＞0 ) ( ∀δ＞0 ) ¬ ( ( ∀x ) ( 0< x−x0＜δ⇒ | f (x)−A|＜ε0 ) )
と書き換えられる、となる。
＊ ＊ ＊
「『…を任意の（すべての）xについて成り立たせること』を成り立たせない」というのは、「…を成り立たせないxが少なくとも一つ存在する」といっても同じことなので、先の命題は、
「 0＜x−x0 ＜δならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ ( x0, x0 ＋δ) ならば、 f(x) ∈ ( A−ε0 , A＋ε0 ) 」
を成り立たせないxを、どんな風に正の実数δをとろうが、少なくとも一つ存在させる
正の実数ε0が(少なくとは一つは)存在する」
と書き換えられる。
厳密に言えば、前の論理式を、¬ ( ∀ A(x) x P(x) )と(∃A(x) x) (¬P(x) )が言い換え可能であることを用いて、
∃ε0＞0 ∀δ＞0 ∃ x ¬ ( 0< x−x0＜δ⇒ | f (x)−A|＜ε0 )
と書き換えられる、となる。
＊ ＊ ＊
「 0＜ x−x0 ＜δならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ ( x0, x0 +δ)ならば、 f(x) ∈ ( A−ε0,A＋ε0) 」
を成り立たせない、とは、
「 0＜ x−x0 ＜δなのに | f(x)−A|＜ε0 でない」
すなわち「 x∈ ( x0, x0 +δ)なのに f(x) ∈ ( A−ε0,A＋ε0) でない」
という命題が成立することであるから、
先の命題は、
「 0＜x−x0 ＜δ なのに、 | f(x)−A|＜ε0 でない」
すなわち「 x∈ ( x0, x0 ＋δ) なのに、 f(x) ∈ ( A−ε0,A＋ε0) でない」
を成り立たせるxを、どんな風に正の実数δをとろうが、少なくとも一つ存在させる
正の実数ε0が(少なくとは一つは)存在する
と書き換えられる。
厳密に言えば、前の論理式を、¬(A⇒B)とA∧¬(B)が書き換え可能であることを用いて、
( ∃ε0＞0 ) ( ∀δ＞0 ) ( ∃ x ) ( 0< x−x0＜δかつ ¬( | f (x)−A|＜ε0 ) )
と書き換えられる、となる。
＊ ＊ ＊
「 | f(x)−A|＜ε0 でない」すなわち「f(x) ∈ ( A−ε0,A＋ε0) でない」は、もちろん、
「 | f(x)−A|≧ε0 である」すなわち「f(x)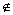 
( A−ε0,A＋ε0) 」 のことだから、
先の命題は、
「 0＜x−x0 ＜δ なのに、 | f(x)−A|≧ε0 」
すなわち「 x∈ ( x0, x0 ＋δ) なのに、 f(x) 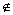( A−ε0,A＋ε0) 」
を成り立たせるxを、どんな風に正の実数δをとろうが、少なくとも一つ存在させる
正の実数ε0が(少なくとは一つは)存在する」
と書き換えられる。
厳密に言えば、
( ∃ε0＞0 ) ( ∀δ＞0 ) ( ∃ x ) ( 0< x−x0＜δかつ ( | f (x)−A|≧ε0 ) ) …(5)
＊ ＊ ＊
先の命題は、
| f(x)−A|≧ε0 すなわち f(x) 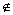( A−ε0,A＋ε0)
を成り立たせるx∈( x0, x0 ＋δ)を、どんな風に正の実数δをとろうが、少なくとも一つ存在させる
正の実数ε0が(少なくとは一つは)存在する」
と書き換えられる。
厳密に言えば、前の論理式を、( ∃A(x) x ) P(x)と∃x ( A(x) ∧ P(x) )が書き換え可能であることを用いて、
( ∃ε0＞0 ) ( ∀δ＞0 ) ( ∃ x∈ ( x0, x0 ＋δ) ) (| f (x)−A|≧ε0)
と書き換えられる、となる。
これは、
δを調整して( x0, x0＋δ)をどうとっても、
( A−ε0 , A＋ε0)の範囲からf(x)を飛び出させるx∈ ( x0, x0 ＋δ)を少なくとも一つ存在させるε0が存在することを、意味している。
以上、「P『(4): f(x)→A (x→x0＋0)』が成り立たない」という仮定の正確な意味を書き下していった。
(step2) 「Pが成り立たない」「(4)が成り立たない」という仮定のもとで、ある数列が存在する。
「Pが成り立たない」「(4)が成り立たない」という仮定は、(5)で示したように、
ε0をうまく選べば、「0< x−x0＜δかつ | f (x)−A|≧ε0 」を満たすxが、その具体的な値などは不明であるもののとにかく、どんなδ>0をとろうとも、確かに存在することを意味していた。
すると、このε0のもとで、「 0< x−x0＜δかつ | f (x)−A|≧ε0」を満たすxばかりをあつめて並べた数列というのも、どんなδ>0をとろうとも、存在することになる。
δはどんな正数でもよいというのだから、たとえば、δ=1/n(nは1以上の自然数)としても、このことは成り立つ。
つまり、
(5)が存在を保証する一定の正数ε0のもとで、各自然数n≧1に対して、
「0＜ xn−x0＜1/n」すなわち「xn ∈ ( x0, x0＋1/n )」を満たし、…(6)
かつ
「| f(xn)−A|≧ε0」すなわち「f(xn ) 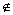( A−ε0 , A＋ε0)」を満たす …(7)
ようなxnが存在する。
厳密にいえば、「(4)が成り立たない」という仮定のもとでは、(5)はδ>0を任意として成立するのだから、
(5)にδ=1/n(自然数n≧1)を入れて、
( ∃ε0＞0 ) ( ∃ xn ) ( 0< xn−x0＜1/n かつ ( | f (xn)−A|≧ε0 ) )
すなわち、 ( ∃ε0＞0 ) ( ∃ xn ∈ ( x0, x0 ＋1/n ) ) (| f (xn)−A|≧ε0)
としても「(4)が成り立たない」という仮定のもとで成り立つことになる。
だから、(5)が存在を保証する一定の正数ε0のもとで、(6) (7)を満たすxnを選んできて、
それを、x1, x2,…xn,…というように並べてつくった数列 { xn }というのも存在することになる。
(step3) 「Pが成り立たない」「(4)が成り立たない」という仮定のもとで存在する「ある数列」が「Qが成り立たない」ことを証明する。
(5)が存在を保証する一定の正数ε0のもとで、(6) (7)を満たすx1, x2,…xn,…を並べた数列 { xn }は、
(6)より(2)(3)を満たしている。
しかし、そのfによる像 f (x1), f (x2),…f (xn),…を並べた数列{ f (xn) }は(7)より
(1): f (xn)→A（ n→∞ ）
すなわち、任意の正の実数εに対して、
「 n≧Nならば、 | f (xn) −A |＜ε 」
を成り立たたせるある自然数Nが存在する (→数列の収束の定義)
を満たさない。
数列{ f (xn) }は、(5)が存在を保証する一定の正数ε0のもとで、| f (xn) −A |≧ε0となるxnをわざわざ選んできて並べた数列であるが、このような数列を存在させるε0が現に存在する以上、
上記の「任意の正の実数εに対して」は言えない。
＊ ＊ ＊
Qは、(2)(3)を満たす全ての数列に対して(1)が成立することを主張する命題であるから、
(2)(3)を満たすのに(1)が成立しないという反例が一つでもあれば、否定される。
(5)が存在を保証する一定の正数ε0と、
そのε0のもとで(6) (7)を満たすx1, x2,…xn,…を並べた数列 { xn }の存在は、そのような反例となる。
＊ ＊ ＊
以上から、Q⇒Pの対偶、すなわち、
結論P「(4): f(x)→A (x→x0＋0)」が成り立たないなら、
仮定Q「(1): f (xn)→A（ n→∞ ）（{ xn }は、(2)(3)を満たす限りで任意の数列）」も成り立たない、
が示された。
ゆえに、Q⇒P、すなわち、
仮定Q「(1): f (xn)→A（ n→∞ ）（{ xn }は、(2)(3)を満たす限りで任意の数列）」が成り立てば、
結論P「(4): f(x)→A (x→x0＋0)」も成り立つ、
が示されたことになる。
（reference）
日本数学会編集『岩波数学辞典（第三版）』項目58関数D族・列(p.158)、項目166収束(pp436).
吉田耕作・栗田稔・戸田宏『平成元年3/31文部省検定済高等学校数学科用 高等学校 微分・積分 新訂版』啓林館、pp.28-33.
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、pp.93-95.
高木貞二『解析概論改訂第3版』岩波書店、1983年、p. 20.
小平邦彦『解析入門I』 (軽装版)岩波書店、2003年 p. 76-79.。
和達三樹『理工系の数学入門コース1:微分積分』岩波書店、1988年、pp.26-34.
吹田・新保『理工系の微分積分学』学術図書出版社、1987年。pp.18-19.22-23.
住友洸（たけし）『大学一年生の微積分学』現代数学社、1987年。pp. 24-26.
杉浦光夫『解析入門I』岩波書店、1980年、pp.50-54, p.60. 極限の定義が特殊なので注意。
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.32-36;42-44..
Fischer,Emanuel.Intermediate Real Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Heidelberg Berlin,1983,pp. 228-231; 238-239.
Lang,Serge.Undergraduate Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1983,pp.135-143.
中内伸光『数学の基礎体力をつけるためのろんりの練習帳』共立出版株式会社、2002年、pp.118-122。