関数の収束と数列の収束の関連性についての定理の証明(普通の極限・片側極限を包括して)
※以下の議論は、
B= (f(x)の定義域)∩{ x |x≠x0}とすると、普通の極限と数列の収束の関係についての議論になり、
∵B= { x |x≠ x0}なら「x∈Bかつ | x−x0 |＜δならば」を
「0＜| x−x0 |＜δならば」と言い換えても同じ。
B= (f(x)の定義域)∩{ x |x＞x0}とすると、右極限、と数列の収束の関係についての議論になり、
∵B= { x |x＞x0}なら「x∈Bかつ | x−x0 |＜δならば」を「0＜x−x0＜δならば」と言い換えても同じ。
B= (f(x)の定義域)∩{ x |x＜x0}とすると、左極限と数列の収束の関係についての議論になる。
∵B= { x |x＜x0}なら「x∈Bかつ | x−x0 |＜δならば」を「−δ＜x−x0＜0ならば」と言い換えても同じ。
[定理]
(設定)
以下で登場するB, x0については、
B：関数f(x)の定義域の部分集合 （つまり、集合Bは定義域に含まれる何らかの区間及びその合併）
x0：x0∈「Bの閉包 (B∪「Bの境界」) 」 （つまり、x0はBで表される区間の内部か境界にある）
※x0は後出の数列 { xn }の第0項という意味ではないので、混乱なきようご注意のほど。
としておく。
(本題)
以下の命題Pと命題Qは互いに言い換え可能（つまりP⇔Q）。
命題P: xがB内でx0に近づくとき、f(x)がAに収束する
すなわち、f(x)→A (x→x0 , x∈B)
あるいは、
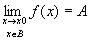
命題Q: ・xn→x0 (n→∞) (つまりx0に収束する) ※x0は後出の数列 { xn }の第0項という意味ではないので注意
かつ、
・任意のn∈N についてxn ∈B 、（つまり全項がBに属する）
を満たす限りで任意につくった(どんな)数列{ xn }に対しても、
f(xn)→A (n→∞) (つまり数列 { f ( xn ) }がAに収束する)
[証明：Ｐ⇒Ｑ]
[杉浦『解析入門I 』p.53]
仮定P： f(x)→A（ x→x0 , x∈B） …(1)
xn→x0（ n→∞ ） …(2)
任意のn∈N についてxn ∈B …(3)
本論：
(step1)仮定(1)の確認。
「xがB内でx0に近づくとき、f(x)がAに収束する」ということの定義に従うと、(1)はすなわち、
任意の（どんな）正の実数εに対して（でも）、
「 x∈Bかつ | x−x0 |＜δならば、 | f(x)−A|＜ε 」
すなわち「 x∈Bかつx0−δ＜x＜x0＋δならば、 A−ε＜ f(x)＜A＋ε 」
すなわち「 x∈ B∩( x0−δ, x0+δ)ならば、 f(x) ∈ ( A−ε,A＋ε) 」
を任意のxについて成り立たせる、ある正の実数δが存在するということ。…(4)
(step2)仮定(2)(3)の確認。
数列の収束の定義に従うと、(2)はすなわち、
任意の（どんな小さな）正の実数ε’に対して（でも）、
「 n≧Nならば、 | xn −x0|＜ε’ 」
すなわち、「 n≧Nならば、 x0−ε’＜ xn＜x0＋ε’ 」
すなわち、「 n≧Nならば、 xn ∈ ( x0−ε’, x0＋ε’) 」
を成り立たたせるある（十分大きな）自然数Nが存在する …(5)
ということ。ただし(3)より、xn ∈B 。
(step3)
ε’はどんな正の実数でもいいというので、
ε’として(4)で定まるδをとっても、(5)はそのまま成り立つ。
すなわち、
(4)で定まった如何なるδに対してであろうとも、
| xn − x0 |＜δ (n≧N)
を成り立たたせるある（十分大きな）自然数Nが存在する …(6)
ということ。ただし(3)より、xn ∈B 。
(step4)
(6)で定まった自然数N以上の項についてみると、
| xn − x0 |＜δ , xn ∈B
が成り立つ。
ならば、(4)より、(6)で定まった自然数N以上の項については、
はじめに決めた任意の正数εに対して
| f(xn)−A|＜ε ( n≧N )
が成り立つといえる。
(step5)仕上げ
数列の収束の定義から、これを以下の様に表現してよい。
f(xn)→A （ n→∞ ）
[証明：Q⇒P]
[杉浦『解析入門I 』p.53]
仮定Q：・f(xn)→A（ n→∞ ） …(1)
ただし、数列 { xn }は、
xn→x0（ n→∞ ） …(2)
任意のn∈N についてxn ∈B …(3)
を満たす限りで任意の数列(をどのようにとってもよい)。
結論P： f(x)→A (x→x0 , x∈B) …(4)
（方針）：Q⇒Pを示すのに、その対偶、すなわち「Pが不成立」⇒「Qが不成立」を示す。
結論P「(4):f(x)→A (x→x0 , x∈B)」が成り立たないなら、
仮定Q「(1): f(xn)→A（ n→∞ ）（{ xn }は、(2)(3)を満たす限りで任意の数列）」も成り立たない、
ことを示す。
本論：
(step1) 「Pが成り立たない」「(4)が成り立たない」という仮定の確認。[中内『ろんりの練習帳』118-121]
「 (4): f(x)→A (x→x0 , x∈B)が成り立たない」と仮定する。
この仮定は、「xがB内でx0に近づくとき、f(x)がAに収束する」の定義を用いて正確にとらえると、
任意の（どんな）正の実数ε0に対して（でも）、
「 x∈Bかつ | x−x0 |＜δならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ B∩( x0−δ, x0+δ)ならば、 f(x) ∈ ( A−ε0,A＋ε0) 」
を任意のxについて成り立たせる、ある正の実数δが存在するということ
の否定、すなわち、¬ ( ( ∀ε0 ＞0 ) ( ∃δ＞0 ) ( ∀x ) ( (x∈B かつ | x− x0|＜δ) ⇒ | f (x)−A|＜ε0) ) となる。
＊ ＊ ＊
これは、
「 x∈Bかつ | x−x0 |＜δならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ B∩( x0−δ, x0+δ)ならば、 f(x) ∈ ( A−ε0,A＋ε0) 」
を任意のxについて成り立たせる、ある正の実数δが、
任意の（どんな）正の実数ε0に対して（でも）、存在するとは限らない
ということを意味するので、
「 x∈Bかつ | x−x0 |＜δならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ B∩( x0−δ, x0+δ)ならば、 f(x) ∈ ( A−ε0,A＋ε0) 」
を任意のxについて成り立たせる正の実数δを存在させないような正の実数ε0が(少なくとは一つは)存在する
と書き換えられる。
厳密に言えば、前の論理式を、¬ ( ∀ A(x) x P(x) )と(∃A(x) x) (¬P(x) )が言い換え可能であることを用いて、
( ∃ε0＞0 ) ¬ ( ( ∃δ＞0 ) ( ∀x ) ( (x∈B かつ | x− x0|＜δ) ⇒ | f (x)−A|＜ε0 ) )
と書き換えられる、となる。
＊ ＊ ＊
「…を成り立たせる正の実数δを存在させない」というのは、「どんな風に正の実数δをとっても…を成り立たせない」といっても同じことなので、先の命題は、
「 x∈Bかつ | x−x0 |＜δならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ B∩( x0−δ, x0+δ)ならば、 f(x) ∈ ( A−ε0,A＋ε0) 」
を任意の(すべての)xについて成り立たせることを、
どんな風に正の実数δをとっても成り立たせない正の実数ε0が(少なくとは一つは)存在する」
と書き換えられる。
厳密に言えば、前の論理式を、¬ ( ∃A(x) x P(x) )と(∀A(x) x) (¬P(x) )が言い換え可能であることを用いて、
( ∃ε0 ＞0 ) ( ∀δ＞0 ) ¬ ( ( ∀x ) ( (x∈B かつ | x− x0|＜δ) ⇒ | f (x)−A|＜ε0 ) )
と書き換えられる、となる。
＊ ＊ ＊
「『…を任意の（すべての）xについて成り立たせること』を成り立たせない」というのは、「…を成り立たせないxが少なくとも一つ存在する」といっても同じことなので、先の命題は、
「 x∈Bかつ | x−x0 |＜δならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ B∩( x0−δ, x0+δ)ならば、 f(x) ∈ ( A−ε0,A＋ε0) 」
を成り立たせないxを、どんな風に正の実数δをとろうが、少なくとも一つ存在させる
正の実数ε0が(少なくとは一つは)存在する」
と書き換えられる。
厳密に言えば、前の論理式を、¬ ( ∀ A(x) x P(x) )と(∃A(x) x) (¬P(x) )が言い換え可能であることを用いて、
( ∃ε0＞0 ) ( ∀δ＞0 ) ( ∃ x ) ¬ ( (x∈B かつ | x− x0|＜δ) ⇒ | f (x)−A|＜ε0 )
と書き換えられる、となる。
＊ ＊ ＊
「 x∈Bかつ | x−x0 |＜δならば、 | f(x)−A|＜ε0 」
すなわち「 x∈ B∩( x0−δ, x0+δ)ならば、 f(x) ∈ ( A−ε0,A＋ε0) 」
を成り立たせない、とは、
「 x∈Bかつ | x−x0 |＜δなのに | f(x)−A|＜ε0 でない」
すなわち「 x∈ B∩( x0−δ, x0+δ)なのに f(x) ∈ ( A−ε0,A＋ε0) でない」
という命題が成立することであるから、
先の命題は、
「 x∈Bかつ | x−x0 |＜δなのに、 | f(x)−A|＜ε0 でない」
すなわち「 x∈ B∩( x0−δ, x0+δ)なのに、 f(x) ∈ ( A−ε0,A＋ε0) でない」
を成り立たせるxを、どんな風に正の実数δをとろうが、少なくとも一つ存在させる
正の実数ε0が(少なくとは一つは)存在する」
と書き換えられる。
厳密に言えば、前の論理式を、¬(A⇒B)とA∧¬(B)が書き換え可能であることを用いて、
( ∃ε0＞0 ) ( ∀δ＞0 ) ( ∃ x ) ( (x∈B かつ | x− x0|＜δ) かつ ¬( | f (x)−A|＜ε0 ) )
と書き換えられる、となる。
＊ ＊ ＊
「 | f(x)−A|＜ε0 でない」すなわち「f(x) ∈ ( A−ε0 , A＋ε0) でない」は、もちろん、
「 | f(x)−A|≧ε0 である」すなわち「f(x)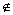 
( A−ε0 , A＋ε0) 」 のことだから、
先の命題は、
「 x∈Bかつ | x−x0 |＜δなのに、 | f(x)−A|≧ε0 」
すなわち「 x∈ B∩( x0−δ, x0+δ)なのに、 f(x) 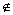( A−ε0,A＋ε0) 」
を成り立たせるxを、どんな風に正の実数δをとろうが、少なくとも一つ存在させる
正の実数ε0が(少なくとは一つは)存在する」
と書き換えられる。
厳密に言えば、
( ∃ε0＞0 ) ( ∀δ＞0 ) ( ∃ x ) ( (x∈B かつ | x− x0|＜δ) かつ ( | f (x)−A|≧ε0 ) )
＊ ＊ ＊
先の命題は、
「 | x−x0 |＜δなのに、 | f(x)−A|≧ε0 」
すなわち「 ( x0−δ, x0+δ)なのに、 f(x) 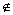( A−ε0,A＋ε0) 」
を成り立たせるx∈Bを、どんな風に正の実数δをとろうが、少なくとも一つ存在させる
正の実数ε0が(少なくとは一つは)存在する」…(5)
と書き換えられる。
厳密に言えば、前の論理式を、( ∃A(x) x ) P(x)と∃x ( A(x) ∧ P(x) )が書き換え可能であることを用いて、
( ∃ε0＞0 ) ( ∀δ＞0 ) ( ∃ x∈B ) ( | x− x0|＜δ かつ | f (x)−A|≧ε0)
と書き換えられる、となる。…(5)
これは、
δを調整して( x0−δ, x0+δ)をどうとっても、
( A−ε0 , A＋ε0)の範囲からf(x)を飛び出させるx∈Bを少なくとも一つ存在させるε0が存在する
ことを、意味している。
以上、「P『(4):f(x)→A (x→x0 , x∈B)』が成り立たない」という仮定の正確な意味を書き下していった。
(step2) 「Pが成り立たない」「(4)が成り立たない」という仮定のもとで、ある数列が存在する。
「Pが成り立たない」「(4)が成り立たない」という仮定は、(5)で示したように、
ε0をうまく選べば、全てのδに対して、「| x− x0|＜δ かつ | f (x)−A|≧ε0 」を満たすx∈Bが、その具体的な値などは不明であるもののとにかく、確かに存在することを意味していた。
すると、全てのδに対して、「| x− x0|＜δ かつ | f (x)−A|≧ε0」を満たすx∈Bばかりをあつめて並べた数列というのも存在することになる。
たとえば、
各自然数n≧1に対して、
「| xn−x0|＜1/n」すなわち「( x0−1/n, x0+1/n )」を満たし、…(6)
かつ
「| f(xn)−A|≧ε0」すなわち「f(x) 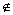( A−ε0 , A＋ε0)」を満たす …(7)
ようなxn∈B とε0が存在することは、 (5)が保証している (δはなんでもよいのだから、δ=1/nとした) 。
だから、(6) (7)を満たすxn∈B とε0を選んできて、
それを、x1, x2,…xn,…というように並べてつくった数列 { xn }⊂Bというのも存在することになる。
(step3) 「Pが成り立たない」「(4)が成り立たない」という仮定のもとで存在する「ある数列」が「Qが成り立たない」ことを証明する。
(6) (7)を満たすx1, x2,…xn,…を並べた数列 { xn }は、(6)より(2)(3)を満たしている。
しかし、そのfによる像を並べた数列{ f (xn) }は(7)より
(1): f (xn)→A（ n→∞ ）
すなわち、任意の（どんな小さな）正の実数εに対して（でも）、
「 n≧Nならば、 | f (xn) −A |＜ε 」
を成り立たたせるある（十分大きな）自然数Nが存在する
を満たさない。数列{ f (xn) }は、| f (xn) −A |≧εとなるxnとε0をわざわざ選んできて並べた数列なのだから。
＊ ＊ ＊
Qは、(2)(3)を満たす全ての数列に対して(1)が成立することを主張する命題であるから、
(2)(3)を満たすのに(1)が成立しないという反例が一つでもあれば、否定される。
(6) (7)を満たすx1, x2,…xn,…を並べた数列 { xn }の存在は、そのような反例となる。
＊ ＊ ＊
以上から、Q⇒Pの対偶、すなわち、
結論P「(4):f(x)→A (x→x0 , x∈B)」が成り立たないなら、
仮定Q「(1): f(xn)→A（ n→∞ ）（{ xn }は、(2)(3)を満たす限りで任意の数列）」も成り立たない、
が示された。
ゆえに、Q⇒P、すなわち、
仮定Q「(1): f(xn)→A（ n→∞ ）（{ xn }は、(2)(3)を満たす限りで任意の数列）」が成り立てば、
結論P「(4):f(x)→A (x→x0 , x∈B)」も成り立つ、
が示されたことになる。
（reference）
日本数学会編集『岩波数学辞典（第三版）』項目58関数D族・列(p.158)、項目166収束(pp436).
吉田耕作・栗田稔・戸田宏『平成元年3/31文部省検定済高等学校数学科用 高等学校 微分・積分 新訂版』啓林館、pp.28-33.
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、pp.93-95.
高木貞二『解析概論改訂第3版』岩波書店、1983年、p. 20.
小平邦彦『解析入門I』 (軽装版)岩波書店、2003年 p. 76-79.。
和達三樹『理工系の数学入門コース1:微分積分』岩波書店、1988年、pp.26-34.
吹田・新保『理工系の微分積分学』学術図書出版社、1987年。pp.18-19.22-23.
住友洸（たけし）『大学一年生の微積分学』現代数学社、1987年。pp. 24-26.
杉浦光夫『解析入門I』岩波書店、1980年、pp.50-54, p.60. 極限の定義が特殊なので注意。
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.32-36;42-44..
Fischer,Emanuel.Intermediate Real Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Heidelberg Berlin,1983,pp. 228-231; 238-239.
Lang,Serge.Undergraduate Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1983,pp.135-143.
中内伸光『数学の基礎体力をつけるためのろんりの練習帳』共立出版株式会社、2002年、pp.118-122。