��` �F n�ϐ��x�N�g���l���̃��R�r�s�� Jacobian Matrix
�y�ݒ�z
n�ϐ�m�l�x�N�g���l��( y1,y2,�c,ym ) = f ( x1,x2,�c,xn ) ���A
�@�@�@m��n�ϐ������l�� �̑g
�@�@�@�@�@y1 = f1 (x1,x2,�c,xn)�@
�@�@�@�@�@y2 = f2 (x1,x2,�c,xn)�@
�@�@�@�@�@�F�@�F�@
�@�@�@�@�@ym = fm (x1,x2,�c,xn)�@
�Ƃ��ĕ\�����Ƃ���B
�܂�A
( y1,y2,�c,ym )=( f1 (x1,x2,�c,xn), f2 (x1,x2,�c,xn),�c, fm (x1,x2,�c,xn) ) = f ( x1,x2,�c,xn)
�Ƃ���B
�y��`�z
�@m��n�ϐ������l�� f1 (x1,x2,�c,xn) , f2 (x1,x2,�c,xn) , �c , fm (x1,x2,�c,xn) �̊e�X���A
�@�e�_��x1,x2,�c,xn �Ɋւ��ĕΔ����\�ł���Ƃ��A
�@mn�́un�ϐ������l�� f1, f2 ,�c, fm ���Γ����v�������B
�@���́Amn���Γ������A
�@�@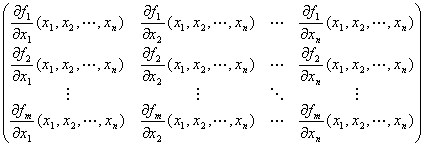
�@�Ƃ����������ɕ��ׂ�m�sn�����s����
�@�u( y1,y2,�c,ym ) = f ( x1,x2,�c,xn )�����R�r�s���v�ƌĂԁB
| �@ |
|||
�y�����z |
�@ |
||
|
�@�E���Y�w��͓����x�U��6�藝6.2-2(p.129);��`2 (p.132). �y�֘A�����z�@�@2�ϐ������l���̃��R�r�s��-���R�r�A��/n�ϐ������l���̃��R�r�s��-���R�r�A�� �y���p��z�@
|
|
||
|
|
|
| �@ |
|||
|
n�ϐ�m�l�x�N�g���l�� ( y1,y2,�c,ym ) = f ( x1,x2,�c,xn )���e�_�������\�Ȃ�A |
�@ |
||
|
�u ( y1,y2,�c,ym ) = f ( x1,x2,�c,xn ) �����R�r�s���v�ɁA�u ( y1,y2,�c,ym ) = f ( x1,x2,�c,xn ) �������v�͓������B |
|
||
|
|
|
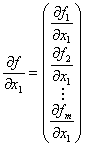 �@�@�@�i
�@�@�@�i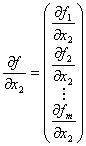 �@�@�@�i
�@�@�@�i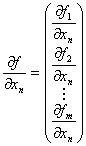 �@�@�@�i
�@�@�@�i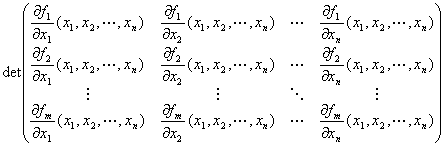 �@
�@