リーマン・スチルチェス積分 Riemann-Stieltjes integral
前:有界変動、スチルチェス積分の定義・性質(1)、
続:性質(2)
→総目次
IV.リーマン・スチルチェス積分可能条件
[杉浦『解析入門I』354--6.; ルディン『現代解析学』6-2~6-9; ]
A. t(x)が単調増加である限りで成り立つ可積分条件。
定義:有界関数f(x)の単調増加関数t(x)に関する過剰和・不足和
[杉浦『解析入門I』354;ルディン『現代解析学』6-2.; ]
cf. リーマン可積分条件の検討におけるfの過剰和・不足和
!!! 閉区間[a,b]で関数f(x)が有界、閉区間[a,b]で関数t(x)が単調増加である場合に限り、!!!
fのtに関する過剰和・不足和を以下のように定義する。
* * *
閉区間Iの分割⊿によって生じた小区間をIk =[xk-1 , xk ] (k=1,2,…,n)で表し、
Ikでのfの下限をmk、上限をMk、すなわち、
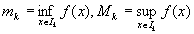
で表し、
t(x)のIkの端点での値の差t(xk)-t(xk-1)を、⊿tkで表すとする。
[注意] t(x)が単調増加とはじめに約束してあるので、⊿tk=t(xk)-t(xk-1)>0
各小区間Ik (k=1,2,…,n)におけるfの下限mkと⊿tkとの積を、全ての区間について足し合わせたものを不足和と呼び、s[⊿]で表す。すなわち、
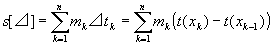
各小区間Ik (k=1,2,…,n) における fの上限Mkと⊿tkとの積を、全ての区間について足し合わせたものを過剰和と呼び、S[⊿]で表す。すなわち、
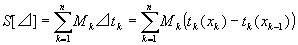
定理:有界関数f(x)の単調増加関数t(x)に関する不足和・過剰和の性質
[杉浦『解析入門I』354.;. ルディン『現代解析学』6-4~6-5.]
1. !!! 閉区間[a,b]で関数f(x)が有界、閉区間[a,b]で関数t(x)が単調増加である場合に限って考える。!!!
f(x)のt(x)に関する不足和・過剰和は、f(x)のt(x)に関するリーマン・スチルチェス和との間に以下の関係が成り立つ。
任意の(どんな)「小区間の代表点{ζk}のとりかた」にたいして(でも、)
s[⊿]≦S [ f ; t ;⊿;{ζk}] ≦S[⊿]
[杉浦『解析入門I』354.;]
2. !!! 閉区間[a,b]で関数f(x)が有界、閉区間[a,b]で関数t(x)が単調増加である場合に限って考える。!!!
細分してゆくほど、f(x)のt(x)に関する不足和は大きくなり、過剰和は小さくなる。
すなわち、⊿≦⊿'ならば、s[⊿]≦s [⊿']、S[⊿]≧S[⊿']。
[杉浦『解析入門I』354.;ルディン『現代解析学』6-4.;]
証明: ルディン『現代解析学』6-4.を参照せよ。
定義:有界関数fの単調増加関数tに関する下積分lower integral
上積分upper integral
[杉浦『解析入門I』354.;ルディン『現代解析学』6-2.; .]
cf. リーマン可積分条件の検討におけるfの下積分・上積分
!!! 以下の議論は、閉区間[a,b]で関数f(x)が有界、閉区間[a,b]で関数t(x)が単調増加である場合に限る。!!!
分割⊿の採り方によって、閉区間 Iにおけるf(x)のt(x)に関する不足和s[⊿]・過剰和S[⊿]の大きさは変わってくる。
特に、不足和・過剰和の性質2.でみたように、分割⊿を細分して行くほど、不足和s[⊿]は大きくなり、過剰和S[⊿]は小さくなる。
このような不足和s[⊿]の上限を、閉区間 Iにおけるf(x) のt(x)に関する下積分と呼び、sで表す。
過剰和S[⊿]の下限を、閉区間 Iにおけるf(x) のt(x)に関する上積分と呼び、Sで表す。
すなわち、閉区間 Iの分割全体の集合をDと表すと、
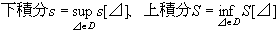
定理:有界関数fの単調増加関数tに関する下積分と上積分の性質
[杉浦『解析入門I』354.; ルディン『現代解析学』6-5.; .]
!!! 閉区間[a,b]で関数f(x)が有界、閉区間[a,b]で関数t(x)が単調増加である場合に限って考える。!!!
1. 閉区間[a,b]におけるf(x) のt(x)に関する下積分s≦上積分S
2. 不足和・過剰和・上積分・下積分の関係
下積分・上積分の定義から、不足和・過剰和との関係も絡めると、
任意の分割⊿の採り方に対して、
閉区間[a,b]におけるf(x) のt (x)に関する不足和s[⊿]≦下積分s≦上積分S≦過剰和S[⊿]
すなわち、 0≦S-s≦S[⊿]-s[⊿] [このかたちは、ルディン『現代解析学』6-6.;]
※利用例:スチルチェス可積分条件:命題A2⇒命題B1の証明
3. 不足和・過剰和・上積分・下積分・スチルチェス和の関係
不足和・過剰和とスチルチェス和の関係:
任意の(どんな)「小区間の代表点{ζk}のとりかた」にたいして(でも)、
s[⊿]≦S [ f ; t ;⊿;{ζk}] ≦S[⊿]
と上記2.の不等式から、
下積分s, 上積分S, スチルチェス和S [ f ; t ;⊿;{ζk}] ∈ [ s[⊿], S[⊿] ] となるから、
任意の(どんな)「小区間の代表点{ζk}のとりかた」にたいして(でも)、
|S-S [ f ; t ;⊿;{ζk}]|≦S[⊿]-s[⊿] 、 |S [ f ; t ;⊿;{ζk}]-s|≦S[⊿]-s[⊿]
[杉浦『解析入門I』356:定理17.7証明のなかで; .]
※利用例:スチルチェス可積分条件:命題A2⇒命題A1の証明
証明: ルディン『現代解析学』6-5.を参照せよ。
定理:
ダルブーの定理はスチルチェス積分では成り立たない。[高木『解析概論』p.132 ;杉浦『解析入門I』355.]
定理:有界関数f(x)の単調増加関数t(x)に関するスチルチェス可積分条件
cf.リーマン積分の可積分条件、
(1) (命題A1:スチルチェス可積分) ⇔ (命題A2) ⇔ (命題A3) [杉浦『解析入門I』355-6; .]
(仮定1) 関数f(x)が閉区間[a,b]上で有界、
かつ、
(仮定2) 関数t(x)が閉区間[a,b]上で単調増加
ならば、
下記 (命題A1:スチルチェス可積分) (命題A2) (命題A3)は互いに同値である。
→証明: A1⇒A2、A2⇒A1、命題A2⇔命題A3
(2) (命題B1:上積分S=下積分s) ⇔ (命題B2) [ルディン『現代解析学』6-6. ]
(仮定1) 関数f(x)が閉区間[a,b]上で有界、
かつ、
(仮定2) 関数t(x)が閉区間[a,b]上で単調増加
ならば、
下記(命題B1:上積分S=下積分s) (命題B2)は互いに同値である。
→証明: B1⇒B2、B2⇒B1
(3) (命題A1:スチルチェス可積分) (命題A2) (命題A3) ⇒(命題B1:上積分S=下積分s) (命題B2)
[杉浦『解析入門I』355-6:例を示す; ルディン『現代解析学』項目6-14.(a); .]
(仮定1) 関数f(x)が閉区間[a,b]上で有界、
かつ、
(仮定2) 関数t(x)が閉区間[a,b]上で単調増加
のもとで、
下記(命題A1:スチルチェス可積分) (命題A2) (命題A3)が成り立つならば、
下記(命題B1: 上積分S=下積分s) (命題B2)も成り立ち、
fのtに関する[a,b]上のスチルチェス積分=fのtに関する上積分S=下積分s
となるが、
下記(命題B1: 上積分S=下積分s) (命題B2)も成り立っていたとしても、
下記(命題A1:スチルチェス可積分) (命題A2) (命題A3)が成りたつとは限らない。
→証明: A2⇒B1 、
(4) [杉浦『解析入門I』355-6:例を示す; ルディン『現代解析学』項目6-14.(a);.]
(仮定1) 関数f(x)が閉区間[a,b]上で有界、
かつ、
(仮定2) 関数t(x)が閉区間[a,b]上で単調増加
かつ、
(仮定3) 関数t(x)が閉区間[a,b]上で連続
のもとでは、
下記 (命題A1:スチルチェス可積分) (命題A2) (命題A3) と(命題B1: 上積分S=下積分s) (命題B2)も同値となって、
fのtに関する[a,b]上のスチルチェス積分=fのtに関する上積分S=下積分s
(5) [高木『解析概論』p.132 ;杉浦『解析入門I』355-6:例を示す; ルディン『現代解析学』項目6-8;6-14.;.]
(仮定1) 関数f(x)が閉区間[a,b]上で有界、
かつ、
(仮定2) 関数t(x)が閉区間[a,b]上で単調増加
かつ、
(仮定3) 関数f(x)が閉区間[a,b]上で連続
ならば、
下記 (命題A1:スチルチェス可積分) (命題A2) (命題A3) (命題B1) (命題B2)が成立し、
fのtに関する[a,b]上のスチルチェス積分=fのtに関する上積分S=下積分s
→証明:仮定1-3⇒命題A3
(命題A1) 関数f(x)は閉区間[a,b]上で関数t(x) に関しスチルチェス積分可能
(命題A2)
[表現1] 閉区間[a,b]の分割⊿を限りなく細かくしていくと、
分割⊿の取り方(つまり、区間Iをn個の小閉区間にわける際の分点のとりかた)によらず、
閉区間[a,b]における関数f(x)の関数t(x)に関する(過剰和-不足和)はゼロに収束する。
[表現2] 記号を用いた簡潔な表現
・|⊿|→0のとき、S[⊿]-s[⊿]→0
ないしは
・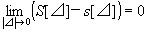
(記号|⊿|→0は、分割の幅が→0なら、そのようなすべての分割の取り方に対して、
という意味。リーマン積分のダルブーの定理の項を参照のこと。)
[表現3] ε-δ法による極限定義に依拠した厳密な表現(→証明で利用可能)
・任意の(どんな)正の実数εに対して(でも)、
「 0<|⊿|<δ ならば、
任意の(分点の取りかたで作れる)分割⊿に対して、|S[⊿]-s[⊿] |<ε 」
を成り立たせる、ある正の実数δが存在する。
つねにs[⊿]≦S[⊿] だから(∵)、絶対値をはずせるので、
・任意の(どんな)正の実数εに対して(でも)、
「 0<|⊿|<δ ならば、
任意の(分点の取りかたで作れる)分割⊿に対して、0≦S[⊿]-s[⊿]<ε 」
を成り立たせる、ある正の実数δが存在する。
としてもよい。
すなわち、( ∀ε>0 ) ( ∃δ>0 ) ( ∀|⊿| ) ( 0<|⊿|<δ⇒ ∀⊿ ( 0≦S[⊿]-s[⊿]<ε) )
(命題A3) 閉区間[a,b]の分割⊿によって生じた各小閉区間Ik (k=1,2,…,n) におけるf(x)の振幅をωkと置く。
また、各小閉区間Ik (k=1,2,…,n) の端点におけるt(x)の値の差を⊿tkと置く(仮定1よりプラス)。
[表現1] 分割⊿を限りなく細かくしていくと、
分割⊿の取り方(つまり、区間Iをn個の小区間にわける際の分点のとりかた)によらず、
積(ωk・⊿tk)をk=1からnまで足し合せた和は0に収束する。
[表現2] 記号を用いた簡潔な表現
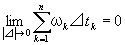
[表現3] ε-δ法による極限定義に依拠した厳密な表現(→証明で利用可能)
・任意の(どんな)正の実数εに対して(でも)、
「 0<|⊿|<δ ならば、
任意の(分点の取りかたで作れる)分割⊿に対して、
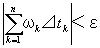 」
」
を成り立たせる、ある正の実数δが存在する。
ここでは、ωk > 0, ⊿ t k>0 なので、
・任意の(どんな)正の実数εに対して(でも)、
「 0<|⊿|<δ ならば、
任意の(分点の取りかたで作れる)分割⊿に対して、
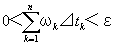 」
」
を成り立たせる、ある正の実数δが存在する。
(命題B1) fのtに関する上積分S= fのtに関する下積分s
(命題B2) [ルディン『現代解析学』6-6. ]
[表現1] 閉区間[a,b]の分割⊿のとり方(区間Iをn個の小閉区間にわける際の分点のとりかた)によって、
閉区間[a,b]における関数f(x)の関数t(x)に関する(過剰和S[⊿]-不足和s[⊿])は変わってくるが、
適当な分割⊿をとることで、(過剰和S[⊿]-不足和s[⊿])を限りなく小さくすることができる。
[表現2] 任意の(どんな)正の実数εに対して(でも)、0≦S[⊿]-s[⊿]<ε
を成り立たせる、ある分割⊿が存在する。
すなわち、( ∀ε>0 ) ( ∃⊿ ) ( 0≦S[⊿]-s[⊿]<ε )
※命題B2は命題A2と一見似ているが、違う。命題B2は、命題A2よりゆるい。
命題A2は、
分割の細かさ(|⊿|)を細かくしていきさえすれば、
分割⊿を行うときの分点をどういう風にとっても必ず、S[⊿]-s[⊿]がゼロに近づく、
という厳しい条件を述べていたのに対して、
この命題B2は、
S[⊿]-s[⊿]がゼロに近づくような、
分割⊿を行うときの分点のとりかたが、少なくとも一つはある、
しかし、それ以外の分割⊿のとりかただと、そうならないかもしれない、
という緩い条件しか述べていない。
※ルディン『現代解析学』におけるスチルチェス積分定義の特殊性:
普通の議論では、
分割⊿を限りなく細かくしたとき、
分割⊿の取り方に関わりなくスチルチェス和が収束することを、スチルチェス積分可能の定義とし、
そのときのスチルチェス和の収束値をスチルチェス積分の定義とするが、
ルディン『現代解析学』項目6-2.は、
「上積分=下積分」の成立(このノートのスチルチェス可積分条件の項の命題4)を「スチルチェス積分可能」の定義とし、
このときの上積分S=下積分sを「スチルチェス積分」の定義としている。
したがって、このノートでは、ルディン『現代解析学』のなかの「スチルチェス積分可能」は、
「上積分S=下積分sの成立が満たされること」に、「スチルチェス積分」は、「上積分S=下積分sという値」と、
置き変えて理解することにする。
※ルディン『現代解析学』における特殊な「スチルチェス積分」定義と、普通のスチルチェス積分定義の関係:
ルディン『現代解析学』は、普通のスチルチェス積分定義と、彼独特の「スチルチェス積分」(=上積分S=下積分s)とが、一致する条件を、項目6-14.において明らかにしている(証明つき)。
1.普通の意味でスチルチェス積分可能ならば、
・ルディンの意味でも「スチルチェス積分可能」(すなわち上積分S=下積分sが成立)
・普通の意味でのスチルチェス積分=ルディンの意味での「スチルチェス積分」(すなわち上積分S=下積分sの値)
だが、逆は必ずしも成りたたない。
この点は、このノートのスチルチェス可積分条件の項で、
命題1が成り立てば命題4も成り立つが、逆は必ずしも成り立たず、
命題4は、命題1の必要条件だが、十分条件ではないと、述べたことと一致する。
2.被積分関数f(x)が連続であるならば、
普通の意味でのスチルチェス積分=ルディンの意味での「スチルチェス積分」(すなわち上積分S=下積分sの値)
3.被積分関数f(x)が、ルディンの意味で「スチルチェス積分可能」(すなわち上積分S=下積分sが成立)、
かつ、
t (x) が積分区間[a,b]で連続であるならば、
普通の意味でのスチルチェス積分=ルディンの意味での「スチルチェス積分」(すなわち上積分S=下積分sの値)
この点は、杉浦『解析入門I』355-6も、
「(t(x)が閉区間[a,b]上で単調増加であるのみならず) t(x)の連続性を仮定しなければ、
上積分S=下積分sが、(普通の意味での)スチルチェス積分のための十分条件にならない(必要条件にはなる)」
と示唆している(証明なし)。
(1)の証明:
・(命題A2) ⇔(命題A3) [杉浦『解析入門I』356;217.. .]
振幅ωk 、過剰和S[⊿] 、不足和s[⊿])の定義から、
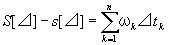
が成立する故に。
すなわち、小区間Ikでのfの下限をmk、上限をMk、とすると、以下のようになる
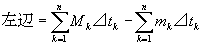
=(M1⊿t1+M2⊿t2+…+Mn⊿tn)-(m1⊿t1+m2⊿t2+…+mn⊿tn)
=(M1⊿t1-m1⊿t1)+(M2⊿t2-m2⊿t2)+…+(Mn⊿tn-mn⊿tn)
=(M1-m1) ⊿t1+(M2-m2) ⊿t2+…+(Mn-mn) ⊿tn
=ω1 ⊿t1+ω2 ⊿t2+…+ωn ⊿tn
=右辺
・(命題A1:スチルチェス可積分) ⇒(命題A2)の証明
リーマン積分の可積分条件における「命題1⇒命題2の証明」と同じ。 [杉浦『解析入門I』356.; .]
・(命題A2)⇒ (命題A1:スチルチェス可積分)の証明 [杉浦『解析入門I』356.; .]
命題A2:任意の(どんな)正の実数εに対して(でも)、
「 0<|⊿|<δ ならば、
任意の(分点の取りかたで作れる)分割⊿に対して、 S[⊿]-s[⊿]<ε 」
を成り立たせる、ある正の実数δが存在する
不足和・過剰和・上積分・スチルチェス和の関係式:
任意の(どんな)「小区間の代表点{ζk}のとりかた」に対して(でも)、
|S-S [ f ; t ;⊿;{ζk}]|≦S[⊿]-s[⊿]
を命題A2の赤字部分の不等式に書き加えると、
命題A2a:任意の(どんな)正の実数εに対して(でも)、
「 0<|⊿|<δ ならば、
任意の「(分点の取りかたで作れる)分割⊿」・「小区間の代表点{ζk}のとりかた」に対して、
|S-S [ f ; t ;⊿;{ζk}]|≦S[⊿]-s[⊿]<ε 」
を成り立たせる、ある正の実数δが存在する
命題A2aの赤字部分を省略してみると、
命題A2b:任意の(どんな)正の実数εに対して(でも)、
「 0<|⊿|<δ ならば、
任意の「(分点の取りかたで作れる)分割⊿」・「小区間の代表点{ζk}のとりかた」に対して、
|S-S [ f ; t ;⊿;{ζk}]|<ε 」
を成り立たせる、ある正の実数δが存在する
命題A2bは、
「関数f (x)は閉区間[a,b]上で関数t(x) に関しスチルチェス積分可能」であることの定義にほかならない。
(命題A2bのSをJとしてみよ。)
(2)の証明:
命題B1⇒命題B2 [ルディン『現代解析学』6-6:;]
・命題B1「 fのtに関する上積分S= fのtに関する下積分s」を仮定し、この上積分S=下積分sをAとおく。
・任意の(どんな)正の実数εに対して(でも)、
S[⊿2]-A<ε/2 、 A-s[⊿1] <ε/2 …①
を成り立たせる、ある分割⊿1、⊿2が存在するので、この分割を採る。
このとき、 S[⊿2]<A+ε/2 、 A < s[⊿1]+ε/2 だから
(「A < s[⊿1]+ε/2」の両辺にε/2を加えて)
S[⊿2]<A+ε/2 < s[⊿1]+ε …②
・分割⊿1の細分であり、なおかつ、分割⊿2の細分でもあるような、分割⊿をとる。…③
すなわち、⊿1≦⊿、⊿2≦⊿。
(つまり、⊿1の分点も⊿2の分点も、分点として継承し、さらにそれ以外にも分点を加えたのが、⊿)
細分と過剰和・不足和の関係式より、S[⊿]≦S[⊿2]、s[⊿1] ≦s [⊿]。…④
・②と④をあわせると、S[⊿]≦S[⊿2] <A+ε/2 < s[⊿1]+ε≦s [⊿] +ε
両端だけに着目すると、S[⊿]<s [⊿] +ε
つまり、S[⊿]-s [⊿]<ε
以上から、命題B1の仮定下で、①と②を満たすような採り方をした分割⊿ならば、
任意の(どんな)正の実数εに対して(でも)、0≦S[⊿]-s[⊿]<εを成り立たせる、
(しかし、任意の分割が、これを成り立たせる保証はない)
すなわち、命題B2が成立する、ことが示された。
命題B2⇒命題B1 [ルディン『現代解析学』6-6:;]
命題B2:任意の(どんな)正の実数εに対して(でも)、
S[⊿]-s[⊿]<ε を成り立たせる、ある分割⊿が存在する
過剰和S[⊿]・不足和s[⊿]・下積分s・上積分Sには大小関係: 0≦S-s≦S[⊿]-s[⊿] が
が常に成り立っているので、
これを利用して、命題B2に下積分sと上積分Sとの関係も書き加えると、
命題B2a:任意の(どんな)正の実数εに対して(でも)、
0≦S-s≦S[⊿]-s[⊿]<ε を成り立たせる、ある分割⊿が存在する
上積分Sと下積分sに注目するために、命題B2aの赤字部分を省略すると、
命題B2b:任意の(どんな)正の実数εに対して(でも)、
0≦S-s<ε を成り立たせる、ある分割⊿が存在する
上積分Sと下積分sはそれに固有の分割⊿'のもとで決まっているので、
上積分Sと下積分sの関係を分割⊿の条件は拘束しない。
よって、
命題B2b':任意の(どんな)正の実数εに対して(でも)、 0≦S-s<ε
定理「 任意の(どんな)正数ε>0に対し(てでも)、ε>a≧0ならば、a=0」を用いると、
命題B2c: S-s=0 すなわち、 S=s
よって、命題B2⇒命題B1が示された。
(3)の証明:
・命題A2⇒命題B1の証明 [杉浦『解析入門I』356.; ルディン『現代解析学』項目6-14.(a);]
命題A2:任意の(どんな)正の実数εに対して(でも)、
「 0<|⊿|<δ ならば、
任意の(分点の取りかたで作れる)分割⊿に対して、0≦S[⊿]-s[⊿]<ε 」
を成り立たせる、ある正の実数δが存在する
過剰和S[⊿]・不足和s[⊿]・下積分s・上積分Sには大小関係: 0≦S-s≦S[⊿]-s[⊿] が
が常に成り立っているので、
これを利用して、命題A2に下積分sと上積分Sとの関係も書き加えると、
命題A2a:任意の(どんな)正の実数εに対して(でも)、
「 0<|⊿|<δ ならば、
任意の(分点の取りかたで作れる)分割⊿に対して、0≦S-s≦S[⊿]-s[⊿]<ε」
を成り立たせる、ある正の実数δが存在する
上積分Sと下積分sに注目するために、命題A2aの赤字部分を省略すると、
命題A2b:任意の(どんな)正の実数εに対して(でも)、
「 0<|⊿|<δ ならば、
任意の(分点の取りかたで作れる)分割⊿に対して、0≦S-s<ε 」
を成り立たせる、ある正の実数δが存在する
上積分Sと下積分sはそれ固有の分割⊿'、|⊿|' のもとで決まっているので、
上積分Sと下積分sの関係を分割⊿、|⊿|の条件は拘束しない。
よって、
命題A2b':任意の(どんな)正の実数εに対して(でも)、 0≦S-s<ε
定理「 任意の(どんな)正数ε>0に対し(てでも)、ε>a≧0ならば、a=0」を用いると、
命題A2c: S-s=0 すなわち、 S=s
よって、命題A2⇒命題B1が示された。
(4)の証明: [ルディン『現代解析学』項目6-14.(b);.]
・仮定1-3のもとで、(命題A1:スチルチェス可積分) ⇔ (命題A2) ⇔ (命題A3)となるのは、 (1)による。
・仮定1-3のもとで、(命題B1:上積分S=下積分s) ⇔ (命題B2)となるのは、 (2)による。
・仮定1-3のもとで、(命題A1) (命題A2) (命題A3) ⇒(命題B1) (命題B2)となるのは、(3)による。
・仮定1-3のもとで、(命題B1: 上積分S=下積分s)⇒(命題A1:スチルチェス可積分)を示す。
(仮定1) 関数f(x)が閉区間[a,b]上で有界、(仮定2) 関数t(x)が閉区間[a,b]上で単調増加
(仮定3) 関数t(x)が閉区間[a,b]上で連続
(仮定4=命題B1) fのtに関する上積分S= fのtに関する下積分s。ここでS= s をAとおく。
step1:任意の正数εに対して、 S[⊿* ]<A+ε/4 を満たすように,分割⊿* をとる。
step2:仮定1より、閉区間[a,b]上では、sup | f (x) | が存在する。
そこで、M= sup | f (x) | ( a≦x≦b ) とおく。
step3:(仮定3) 関数t(x)が閉区間[a,b]上で連続 は、
定理より、関数t(x)が閉区間[a,b]上で一様連続であることを意味する。
すなわち、任意の正数ηに対して、
| x-x0| < δ (∀ x,x0∈[a,b] ) ⇒ | t(x)-t(x0)|<η
を成り立たせる、ある正数δが存在する。…①
step4:任意の正数ε、M,nから決めたε/4Mnは正値であるので、①のηのとりうる値の一つと考えてよい。
よって、任意の正数εから②式で決めたη' に対して、
| x-x0| < δ' (∀ x,x0∈I ) ⇒ |t (x)-t (x0)|<ε/4Mn
を成り立たせる、ある正数δ' が存在する。…②
step5:
0<|⊿|<δ’ならば、任意の(分点の取りかたで作れる)分割⊿に対して、
分割⊿によって生じたすべての小閉区間Ik( k=1,2, …,n ) において、
t(x)のIk両端値の差⊿tk =t(xk)-t(xk-1) について、
⊿tk<ε/4Mn ( k=1,2, …,n )
が成り立つ。
なぜなら、0<|⊿|<δ’とした⊿によって生じた小区間Ik ( k=1,2, …,n )の幅は、どれも、δ’より小さい、
ゆえに、②より、各小区間Ik ( k=1,2, …,n )におけるtの値の差は、大きくてもせいぜいε/4Mn にとどまる。
(この先、ぼくには、理解できない。)
(5)の証明: [高木『解析概論』p.132 ;ルディン『現代解析学』項目6-8;6-14.; 杉浦『解析入門I』定理17.8(p.356.);]
・仮定1-3のもとで、(命題A1:スチルチェス可積分) ⇔ (命題A2) ⇔ (命題A3)となるのは、 (1)による。
・仮定1-3のもとで、(命題B1:上積分S=下積分s) ⇔ (命題B2)となるのは、 (2)による。
・仮定1-3のもとで、(命題A1) (命題A2) (命題A3) ⇒(命題B1) (命題B2)となるのは、(3)による。
・(仮定1) (仮定2) (仮定3) ⇒命題A3 を示す。
[前半]
step1: (仮定3) 関数f(x)が閉区間[a,b]上で連続
は、定理より、関数f(x)が閉区間[a,b]上で一様連続であることを意味する。
すなわち、任意の正数ηに対して、
| x-x0| < δ (∀ x,x0∈[a,b] ) ⇒ | f(x)-f(x0)|<η
を成り立たせる、ある正数δが存在する。…①
step2: 任意の正数εに対して、η' を以下のように決める。
η' < ε/{ t (b) - t (a) } …②
なお、(仮定2) 関数t(x)が閉区間[a,b]上で単調増加より、
t (b) - t (a)>0 。
そして、εも正数だから、
η'は正数。 …③
step3: 任意の正数εから②式で決めたη'は③より、①のηのとりうる値の一つと考えてよい。
よって、任意の正数εから②式で決めたη' に対して、
| x-x0| < δ' (∀ x,x0∈I ) ⇒ | f(x)-f(x0)|<η'
を成り立たせる、ある正数δ' が存在する。…④
[後半] 命題A3 :任意の(どんな)正の実数εに対して(でも)、
「 0<|⊿|<δ ならば、
任意の(分点の取りかたで作れる)分割⊿に対して、
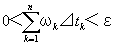 」
」
を成り立たせる、ある正の実数δが存在する
を示すには、これを満たすδの一つをあげればよいわけだが、
これを満たすδの一つが、④で存在することが確認されたδ’ である。
以下、④で存在することが確認されたδ’が、任意の(どんな)正の実数εに対して(でも)、
「 0<|⊿|<δ’ならば、任意の(分点の取りかたで作れる)分割⊿に対して、
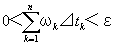 」
」
を成り立たせる、ことを示す。
Step1: 0<|⊿|<δ’ならば、任意の(分点の取りかたで作れる)分割⊿に対して、
分割⊿によって生じたn個の小閉区間Ik( k=1,2, …,n ) におけるfの上限Mk・下限mk( k=1,2, …,n )の間に、
Mk - mk ≦ η' ( k=1,2, …,n ) …⑤
が成り立つ。
なぜなら、0<|⊿|<δ’とした⊿によって生じた小区間Ik ( k=1,2, …,n )の幅は、どれも、δ'より小さい、
ゆえに、④より、各小区間Ik ( k=1,2, …,n )におけるfの値の差は、大きくてもせいぜいη' にとどまる。
Step2:各小閉区間 Ikの振幅ωk= Mk- mk ( k=1,2, …,n )を用いて、⑤を書きかえると、
0<|⊿|<δ’ならば、任意の(分点の取りかたで作れる)分割⊿に対して、
分割⊿によって生じたn個の小閉区間Ik( k=1,2, …,n ) におけるfの振幅ωk ( k=1,2, …,n )について、
ωk≦ η' ( k=1,2, …,n ) …⑥
が成り立つ
となる。
Step3: 0<|⊿|<δ’ならば、任意の(分点の取りかたで作れる)分割⊿に対して、
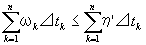 (∵⑥)
(∵⑥)
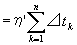
= η'{ t (b)-t (a) } (∵ 仮定2:関数t(x)が閉区間[a,b]上で単調増加)
<ε (∵②)
が成り立つ。
B. t(x)が単調増加という条件を、
t(x)が有界変動関数という条件まで緩めても成り立つ可積分条件。
定理:閉区間[a,b]上で連続な関数f(x)は、閉区間[a,b]で、
任意の有界変動関数t(x) に関しスチルチェス積分可能である。
[杉浦『解析入門I』356.; ルディン『現代解析学』項目6-28. ]
(証明) [杉浦『解析入門I』356.; .]
step1:「有界変動関数は二つの単調増加関数の差で表せる」という定理より、
t(x)は、xのなんらかの単調増加関数φ(x)、ψ(x)を用いて、
t(x)=φ(x)-ψ(x) …①
と置ける。
Step2:関数f(x)は[a,b]上で連続、φ(x)、ψ(x)は、単調増加関数だから、定理より、
f(x)はφ(x) に関しスチルチェス積分可能、f(x)はψ(x) に関しスチルチェス積分可能。
Step3:スチルチェス積分の線形性より、
関数f(x)は、閉区間I [a,b]上で関数φ(x)-ψ(x)に関しスチルチェス積分可能となり、
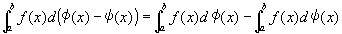
step4:①を用いて、φ(x)、ψ(x)をもとのt(x)にもどすと、
関数f(x)は、閉区間I [a,b]上で関数t(x)に関しスチルチェス積分可能となり、
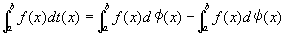
※右辺の単調増加関数に関するスチルチェス積分で、左辺の有界変動関数に関するスチルチェス積分を定義した、といったほうが、正確かもしれない。
定理:
閉区間[a,b]上の有界変動関数t(x)は、
閉区間[a,b]上の任意の連続な関数fに関し閉区間[a,b]上スチルチェス積分可能である。[杉浦『解析入門I』356.; .]
(証明) 部分積分公式と「連続関数は有界変動関数に関し可積分」から。 [杉浦『解析入門I』356-7.; .]
(reference)
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.93-99;104-106.
高木貞治『解析概論:改訂第3版』岩波書店、1983年、pp. 129-132;443-445.
杉浦光夫『解析入門I』東京大学出版会、1980年、p.345;pp.349-361.
Walter Rudin,Principles of Mathematical Analysis,Mcgraw-Hill,1953-1976.
=ウォ-ルタ-・ルディン『現代解析学』共立出版、1971年、第6章。
Lang,Serge.Undergraduate Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1983,pp.224-5:Exercisesとして。
Lang,Serge.Real and Functional Analysis(Graduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1993,pp.278-287.
Ross,Kenneth A.Elementary Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1980,pp.203-221.