Line fitting of y = a + bx: Errors in both y and x
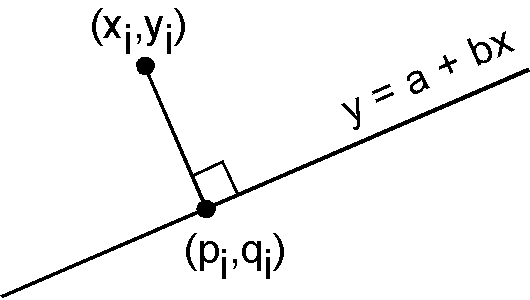 Quantity to be minimized is,
\[ t = \sum_{i=1}^n \{(x_i - p_i)^2 + (y_i - q_i)^2\}. \]
It is easily shown that,
\[ t = \frac{1}{b^2 + 1} \sum_{i=1}^n (y_i - a - bx_i)^2. \]
From \(\partial t/\partial a = 0\), we obtain \(a = \bar y - b\bar x\), where \(\bar x = \sum_{i=1}^n x_i/n\) and \(\bar y = \sum_{i=1}^n y_i/n\). Hence, \(t\) is given by,
\begin{eqnarray*}
t & = & \frac{1}{b^2+1}\sum_{i=1}^n \{(y_i - \bar y) - b(x_i - \bar x)\}^2, \\
& = & \frac{1}{b^2+1}\sum_{i=1}^n (v_i - bu_i)^2,
\end{eqnarray*}
where \(u_i = x_i - \bar x\), \(v_i = y_i - \bar y\). Setting \(\partial t/\partial b = 0\) and denoting \(S_{uu} = \sum_{i=1}^n u_i^2, S_{vv} = \sum_{i=1}^n v_i^2, S_{uv} = \sum_{i=1}^n u_i v_i\), we obtain,
\[ S_{uv}b^2 - (S_{vv} - S_{uu})b - S_{uv} = 0. \]
Solving this equation, \(b\) is given by,
\begin{equation}
b = \frac{(S_{vv} - S_{uu}) \pm \sqrt{(S_{vv} - S_{uu})^2 + 4S_{uv}^2}}{2S_{uv}}. \label{eq01}
\end{equation}
Quantity to be minimized is,
\[ t = \sum_{i=1}^n \{(x_i - p_i)^2 + (y_i - q_i)^2\}. \]
It is easily shown that,
\[ t = \frac{1}{b^2 + 1} \sum_{i=1}^n (y_i - a - bx_i)^2. \]
From \(\partial t/\partial a = 0\), we obtain \(a = \bar y - b\bar x\), where \(\bar x = \sum_{i=1}^n x_i/n\) and \(\bar y = \sum_{i=1}^n y_i/n\). Hence, \(t\) is given by,
\begin{eqnarray*}
t & = & \frac{1}{b^2+1}\sum_{i=1}^n \{(y_i - \bar y) - b(x_i - \bar x)\}^2, \\
& = & \frac{1}{b^2+1}\sum_{i=1}^n (v_i - bu_i)^2,
\end{eqnarray*}
where \(u_i = x_i - \bar x\), \(v_i = y_i - \bar y\). Setting \(\partial t/\partial b = 0\) and denoting \(S_{uu} = \sum_{i=1}^n u_i^2, S_{vv} = \sum_{i=1}^n v_i^2, S_{uv} = \sum_{i=1}^n u_i v_i\), we obtain,
\[ S_{uv}b^2 - (S_{vv} - S_{uu})b - S_{uv} = 0. \]
Solving this equation, \(b\) is given by,
\begin{equation}
b = \frac{(S_{vv} - S_{uu}) \pm \sqrt{(S_{vv} - S_{uu})^2 + 4S_{uv}^2}}{2S_{uv}}. \label{eq01}
\end{equation}
However, to analyze an Arai plot in paleointensity studies, we usually do not use this method or the one presented in the previous page. Instead, a special solution of York (1966) is used as described in the next page.